Адаптивное управление

Адаптивным называется такое управление, алгоритм и программа работы которого изменяются в зависимости от изменения внешних условий. Системы, в которых реализуется адаптивное управление, называются адаптивными. Они подразделяются на два вида - самонастраивающиеся и самоорганизующиеся. В самонастраивающихся системах при изменении внешних условий изменяются только алгоритмы и программы управления, а в самоорганизующихся системах при изменении внешних условий изменяются как алгоритмы и программы управления, так и структурная схема управления. Такие системы относятся к классу сложных систем.

4. Основные виды регуляторов в аналоговых сау.

Входной сигнал х в устройстве управления УУ преобразуется в сигнал u, который воздействует на объект управления ОУ. Функция преобразования сигнала х в сигнал u определяет тип регулятора в УУ.

Самым простым регулятором является пропорциональный регулятор, у которого сигнал u прямо пропорционален сигналу х, т.е. u(t) = kx(t), где k - коэффициент пропорциональности. Типичным пропорциональным регулятором является усилитель мощности. В интегральном регуляторе или просто интеграторе сигнал u пропорционален интегралу по времени от сигнала х, , где- постоянная времени интегратора.

В дифференциальном регуляторе или просто дифференциаторе сигнал пропорционален производной от сигнала х по времени: , где- постоянная времени дифференциатора.

В пропорционально-интегральном регуляторе сигнал u пропорционален как сигналу х, так и интегралу по времени от него .

В пропорционально-дифференциальном регуляторе сигнал u пропорционален как сигналу х, так и производной по времени от него .

В пропорционально-интегрально-дифференциальном регуляторе сигнал u зависит от сигнала х, от интеграла его по времени и от производной его по времени .

Такие регуляторы применяются в системах, где надо отслеживать быстрые, умеренные и медленные изменения входного сигнала. На рис.1.9 приведена структурная схема такого регулятора.

Структурная схема пропорционально-интегрально-дифференциального регулятора.

5. Описание сау с помощью дифференциальных уравнений. Классификация сау по коэффициентам дифференциальных уравнений. Линеаризация сау.

см вопрос 7

6. Преобразование Лапласа (прямое и обратное) и его основные теоремы. Примеры. Прямое и обратное преобразования Лапласа

Преобразования Лапласа играют очень важную роль при исследовании систем, описываемых дифференциальными уравнениями. С помощью прямого преобразования Лапласа можно перейти от дифференциальных уравнений к алгебраическим, решить их в алгебраической форме, а затем с помощью обратного преобразования получить искомый результат.

Прямое преобразование Лапласа осуществляется по формуле: , (2.1) где- комплексная переменная.

На функцию x(t) накладываются некоторые ограничения /3/. Иногда для простоты пользуются символической записью выражения (2.1) в виде: , где L - оператор прямого преобразования Лапласа.

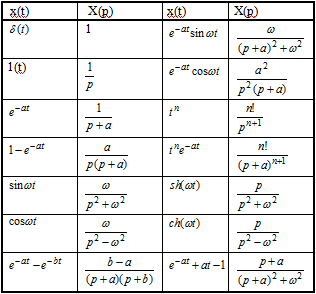
Функция x(t) называется оригиналом, а Х(р) - изображением. В таблице 2.1 приведены преобразования Лапласа для некоторых функций х(t). Кроме прямого существует также и обратное преобразование Лапласа, определяемое по формуле: , (2.2) где интеграл берется на комплексной плоскости р вдоль любой прямой. Символически операцию обратного преобразования Лапласа по (2.2) записывают в виде:.

Обратное преобразование Лапласа можно определить по (2.2), из табл. 2.1, а также с помощью теоремы вычетов, из которой следует соотношение: где- вычеты подынтегральной функцииn - число полюсов функциигде она обращается в бесконечность.

Вычет в простом полюсе определяется по формуле: а вычет в полюсе кратности k:

Таблица 2.1