Рівняння руху простих механічних коливань систем:

а) Математичний маятник – це система, яка є матеріальною точкою (металевою кулькою), підвішеною на тонкій невагомій і нерозтяжній нитці.

Якщо кульку відхилити на деякий кут , то рівнодійна силасил натягуі земного тяжіннянамагається повернути кульку в положення рівноваги. Вертальна сила:

Рис. 5.14.

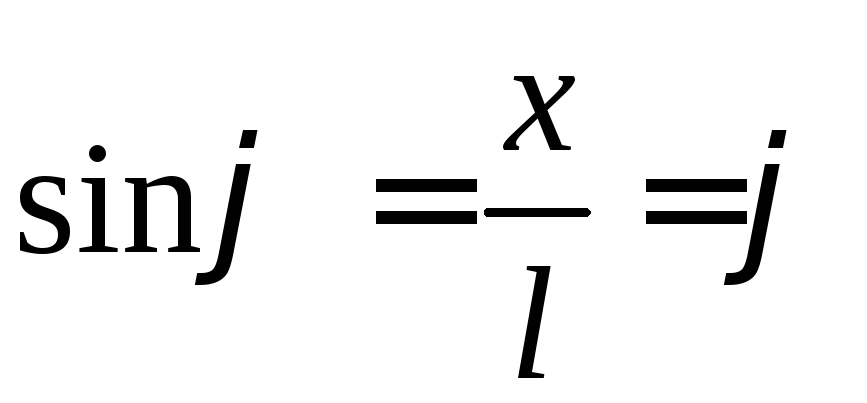Оскільки залежність такої сили від кута нелінійна, то коливання маятника не будуть гармонічними. Для малих кутівможна записати, щоі вираз вертальної сили запишеться як:

Таким чином при малих кутах відхилення маятника тангенціальна сила пропорційна відхиленню х і направлена в бік протилежний напряму відхилення. Отже, сила є квазіпружною, а коливання маятника – гармонічними. Порівнюючи k = mω₀²;

тоді:

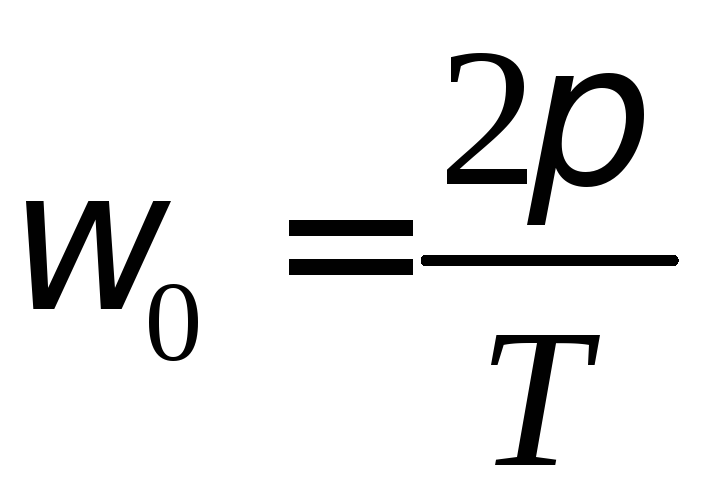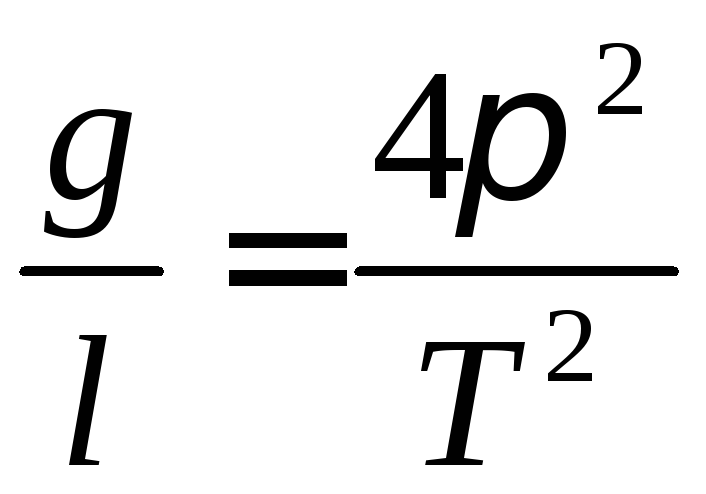
;  (5-10б)

Звідси випливає, що період коливань математичного маятника не залежить від амплітуди коливань і маси маятника, а визначається його довжиною і прискоренням вільного падіння тіл у даному місці Землі.

Рівняння руху математичного маятника матиме такий вигляд

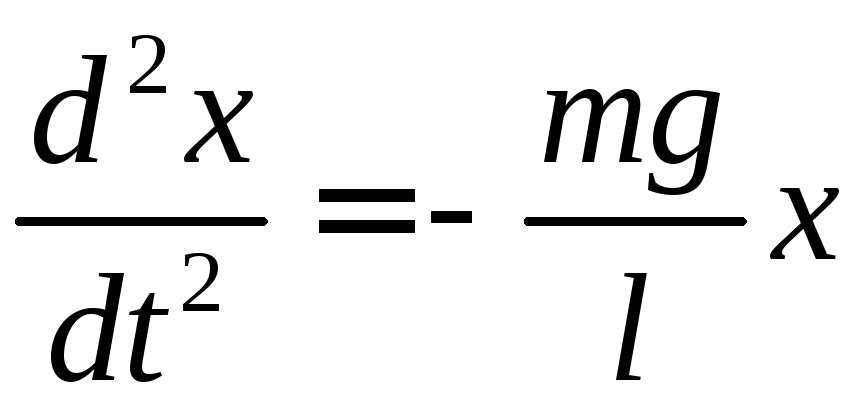
Знак мінус вказує на те, що вертальна сила напрямлена до положення рівноваги.

З іншого боку обертаючий момент:

Динамічне рівняння руху: ;;;

; ;;;

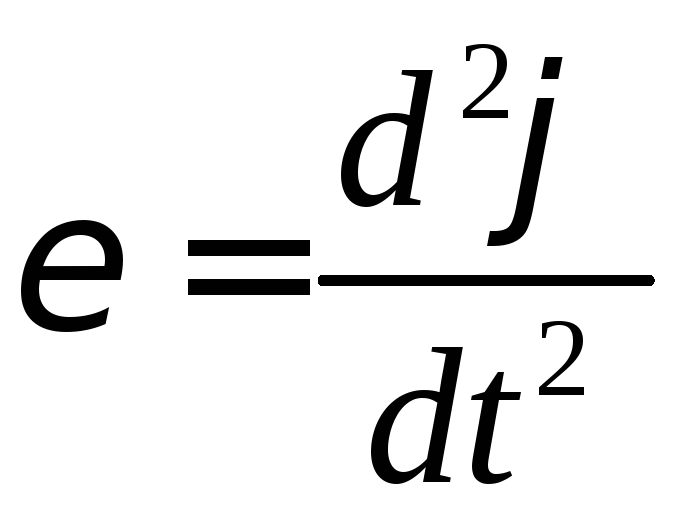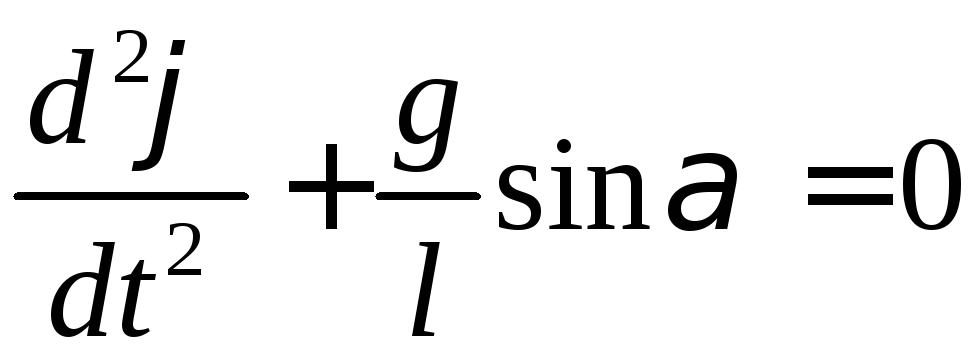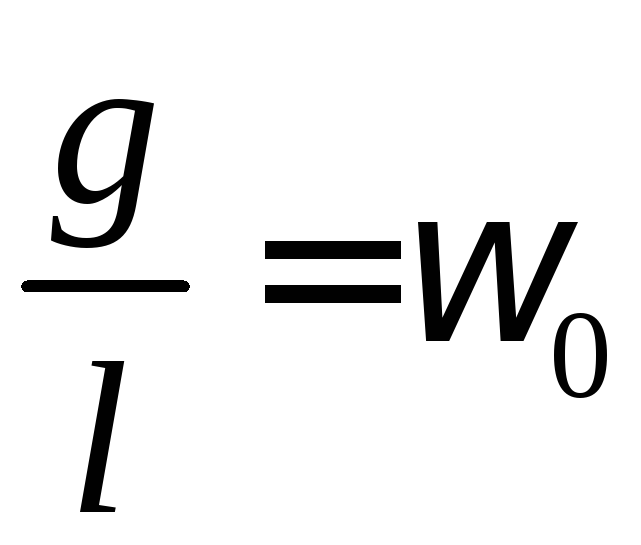(5-11)

Рішення цього рівняння:

Якщо точку, що коливається, не можна представити, як матеріальну точку, маятник називається фізичним.

б) Фізичний маятник – тверде тіло, що має нерухому вісь обертання, яка не проходить через його центр мас (рис. 5.15).

Будучи виведеним з положення рівноваги, тіло здійснює біля осі крутильні коливання.

Обертаючий момент

Знак мінус вказує на те, що повертаючий момент намагається повернути маятник до положення рівноваги, а кут відхилення від положення рівноваги відрахову-ється у протилежному напрямі.

Рис. 5.15.

При малих кутах .

I – момент інерції відносно осі обертання.

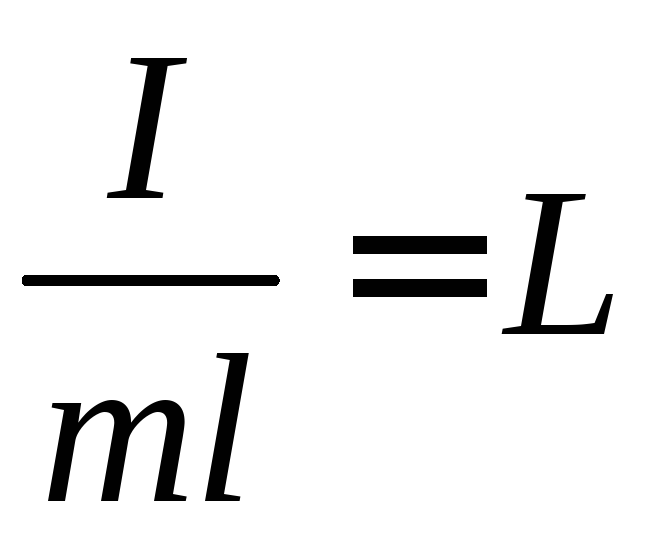–зведена довжина фізичного маятника – це довжина такого математичного маятника, який має такий же період коливання, що і даний фізичний маятник.

Обертальний момент:

;

; ;;;

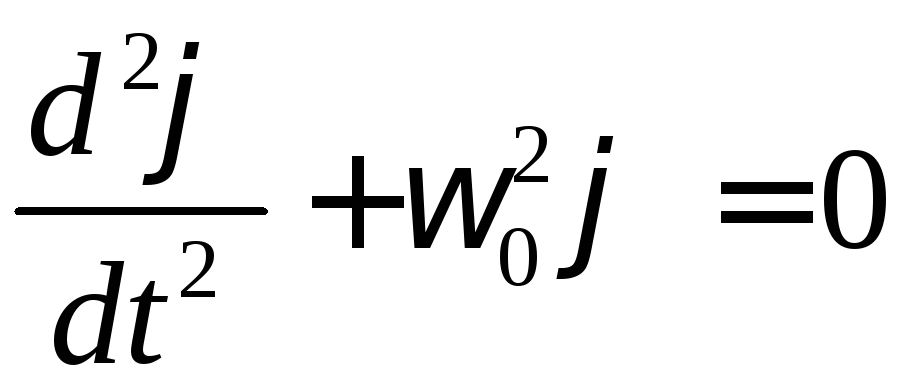(5-12)

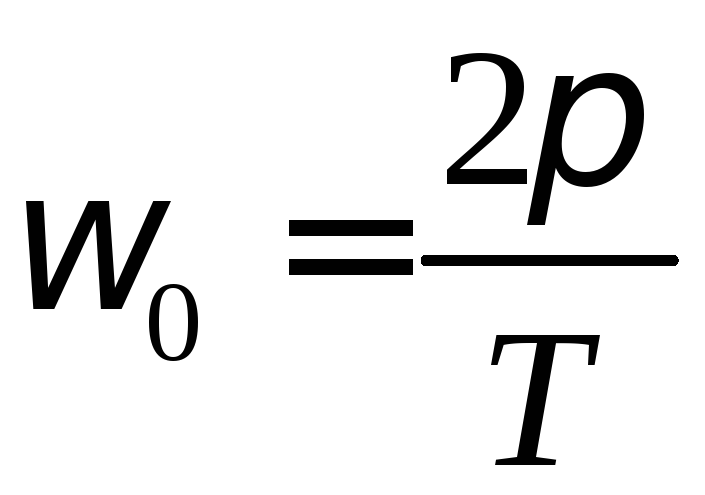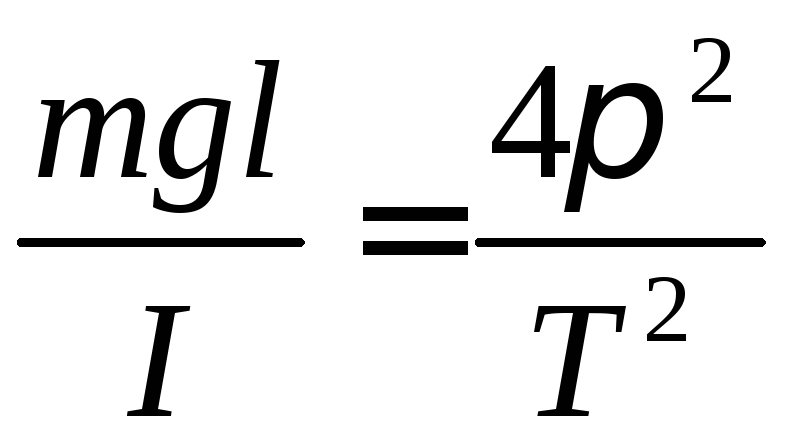; ; (5-13)

Коливальні системи та їх енергія.

Механічні системи, які володіють такою властивістю, що будучи виведеними з положення стійкої рівноваги, а потім відпущені, створюють коливання, що називається коливальними системами, а створені ними коливання – власними.

Якщо сили тертя відсутні, то власні коливання називаються вільними.

Енергія коливальної системи складається з кінетичної енергії рухомого елементу системи і потенціальної енергії пружної частини системи:

;

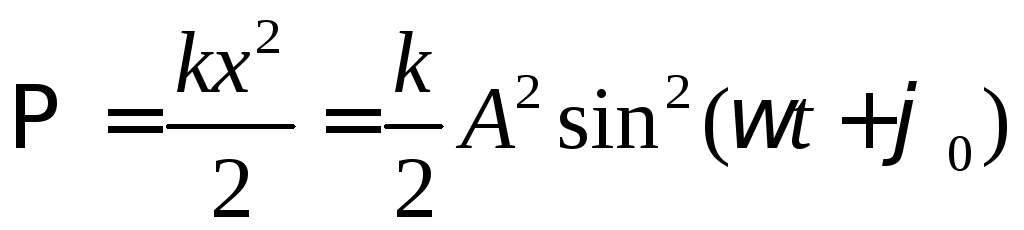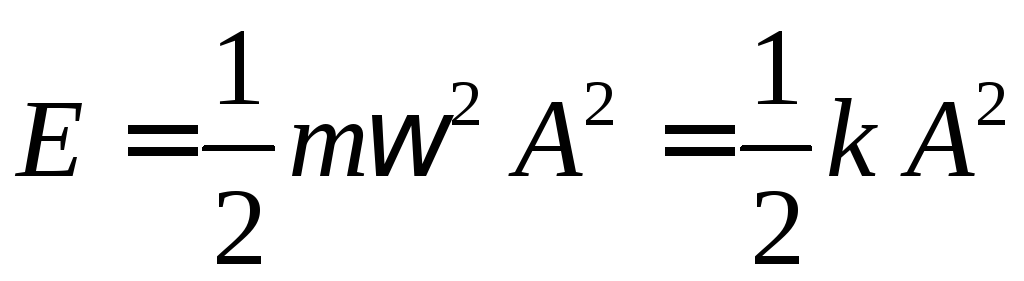(5-14)

Висновок: кінетична і потенціальна енергії здіснюють гармонічні коливання, але циклічна частота коливань енергії вдвічі більша від циклічної частоти коливань зміщення. Механічна енергія гармонічних коливань пропорційна квадрату амплатуди коливань зміщення і з часом не змінюється.

Динамічне рівняння вільних (власних) гармонічних коливань.

У випадку вільних коливань на рухомий елемент системи діє квазіпружна сила , використовуючи рівняння другого закону Ньютона:

; ;;;;

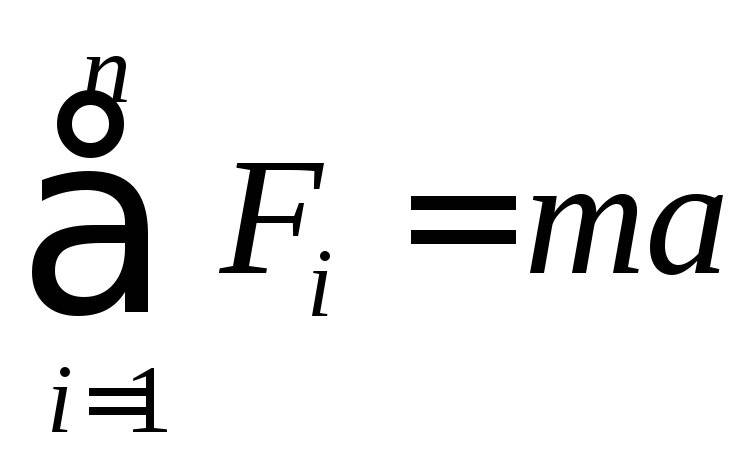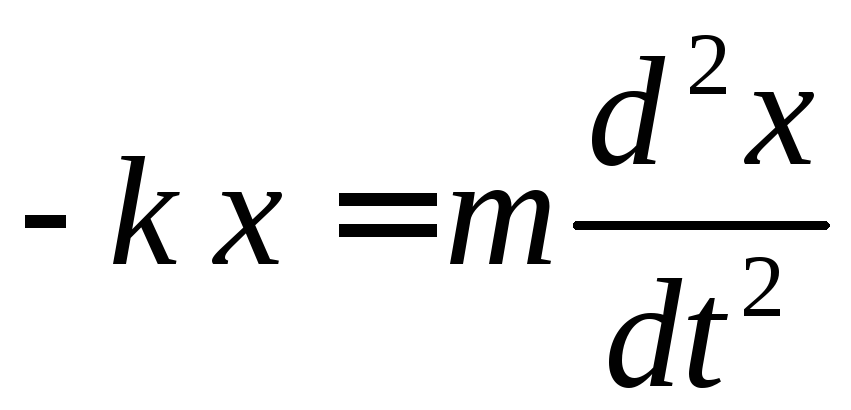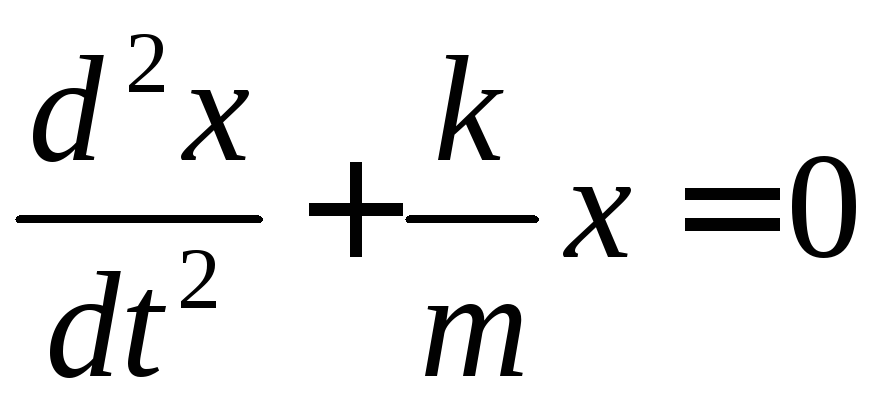Отримуємо динамічне рівняння руху:

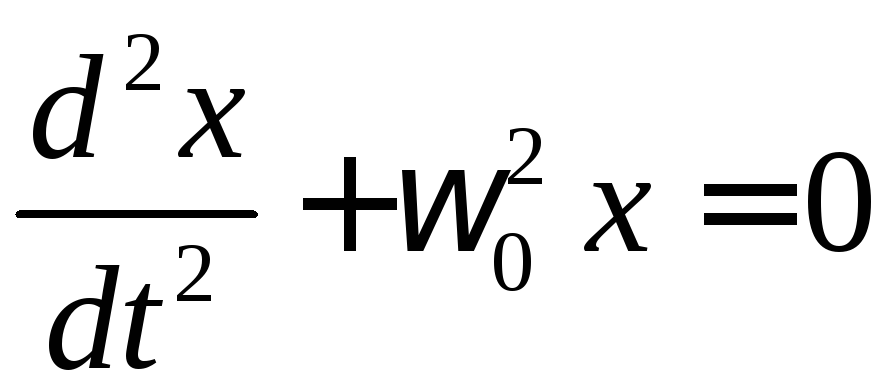–рівняння руху (лінійне однорідне диференціальне рівняння другого порядку).

Загальний розв’язок:

теорія диференціальних рівнянь дає таке рішення , що можна перевірити безпосередньо підставивши його в рівняння руху (5-11). З розв’язку диференційного рівняння одержуємо:

; .

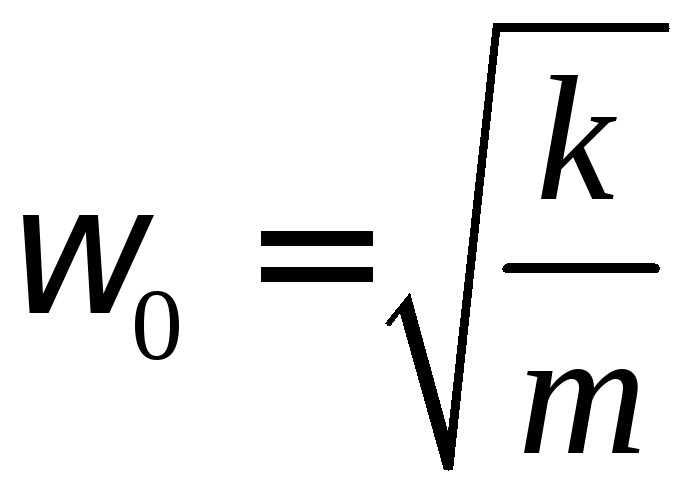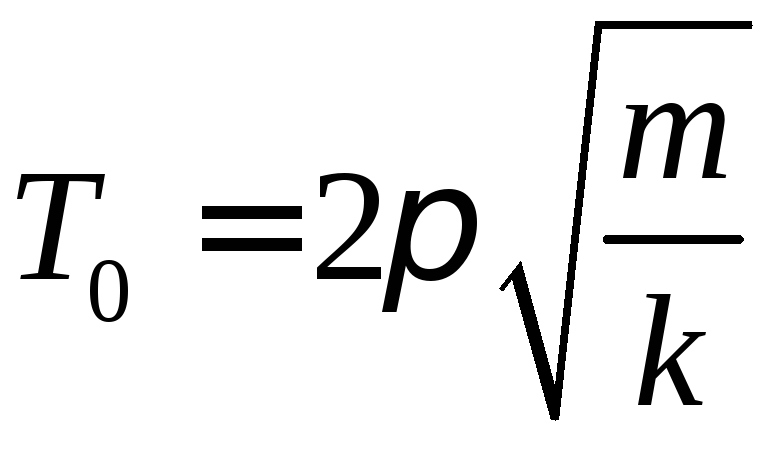Тобто, якщо на рухомий елемент системи діє пружна (квазіпружна) сила, то він здійснює гармонічні коливання з постійною амплітудою і частотою, а його розв’язком якого є гармонічна функція

Гармонічні коливання діляться на вільні і згасаючі.

Вільні коливання – коливання, які відбуваються без впливу зовнішнього середовища, в якому вони здійснюються.