RADIATION THERAPY TREATMENT PLANNING, MONTE CARLO CALCULATIONS IN

CHEN-SHOU CHUI

ELLEN YORKE

REN-DIH SHEU

Memorial Sloan-Kettering

Cancer Center

New York City, New York

INTRODUCTION

Boltzmann Transport Equation

The distribution of radiation in a three-dimensional (3D) heterogeneous medium is governed by the Boltzmann transport equation, which is a partial differential integral equation in six dimensions [3D for position, two (2D) for direction, and one (1D) for energy].

Due to the complex nature of the Boltzmann transport equation, analytic solutions are generally not available except for very simple, idealized cases. For realistic problems, numerical methods are needed. The Monte Carlo method is probably the most accurate and widely used method for solving radiation transport problems in 3D, heterogeneous geometry.

Random Sampling, Law of Large Numbers, Central Limit

Theorem

The basic idea of the Monte Carlo method is to simulate physical events by random sampling from known probability distributions. For example, the step size a photon particle travels before the next interaction is sampled from the exponential distribution. The particular interaction event is sampled from the relative probabilities of competing interaction types. If a Compton event occurs, the energy and direction of the outgoing photon and electron are sampled from the Klein–Nishina distribution.

There are two mathematical principles underlying the Monte Carlo method: (1) The law of large numbers, and (2) the central limit theorem. The law of large numbers says that as the sample size increases to infinity, the sample average approaches the mean of the probability distribution from which the samples were drawn. Since in practice the sample size is finite, the error of the sample average needs to be estimated. For this, we make use of the central limit theorem, which states that the distribution of the sample averages approaches a normal distribution if the sample size is sufficiently large. Moreover, the standard deviation of the mean is inversely proportional to the square root of the total number of histories. Thus, in order to reduce the standard deviation of the mean by a factor of 2, the number of histories needs to be increased by a factor of 4. To estimate the statistical uncertainty, it is common practice to divide the total number of histories into separate groups, with each group containing sufficiently large number of histories. The sample average of each group, according to the central limit theorem, is normally distributed. The standard deviation of the mean is then calculated from these group averages. Alternatively, a history-by- history method can be used to estimate the standard

deviation of the mean. In this method, both the quantity of interest and its square are tallied on the fly for each history. After the simulation is completed, the standard deviation of the mean is then calculated using the sum and the sum of squares of all histories. This method tends to have smaller uncertainty in the uncertainty estimate than the multiple group method.

Applications of Monte Carlo Method in Medical Physics

The Monte Carlo method has been applied to a variety of medical physics problems (1). For radiation therapy, these include the simulation of the machine head (2–22); dose calculation for external photon beams (23–38); electron beams (39–49); proton beams (50–54); and brachytherapy (55–86). For nuclear medicine, it has been used to calculate organ doses due to internal emitters (87–97). For diagnostic radiology, it is used for calculating beam characteristics and dosimetry (98–111). For radiation measurement, various correction factors for ion chambers have been calculated with Monte Carlo (112–129).

A number of Monte Carlo codes have been developed and applied to problems in medical physics (39,43,130– 141). For the purpose of radiation therapy treatment planning, the EGS4 system and its user codes (43,130,133,135) are probably the most widely used in North America.

MONTE CARLO SIMULATION

Overview

A Monte Carlo simulation consists of two major components: transport and interaction. Transport moves a particle from one position to another while interaction determines the outcome of a particular interaction event. If an interaction results in multiple outgoing particles, as in the case of Compton scattering or pair production, then each outgoing particle forms its own transport- and-interaction track. This repetitive transport-and- interaction continues until either the particle travels out of the geometry, for example, exiting the patient body, or its energy falls below a cutoff energy.

Geometry Specification

For a given Monte Carlo simulation, the 3D geometry needs to be described by a collection of mathematical objects. One such package, called combinatorial geometry (142) has been used by a number of Monte Carlo codes. The combinatorial geometry package provides a set of primitive objects, such as sphere, cylinder, box, cone, and so on. An object in question is then modeled by logical combinations of these primitives. For example, a hemisphere can be formed as an intersection of a sphere and a box. The physical properties of the object are also assigned, including the material composition and the physical density. The combinatorial geometry package is a powerful tool that can be used to define very complex geometric objects such as the treatment machine head.

If a 3D image set, such as computed tomography (CT), is used for dose calculation, then the entire 3D voxel array defines the geometry. Since the CT image is typically

acquired with kilovoltage X rays, when it is used for dose calculation for megavoltage photons or electrons, the CT Hounsfield number needs to be converted into electron density ratios relative to water. For radiation therapy dose calculations, the typical energy range is up to 20 MeV and the physical properties of the voxel can often be considered as water equivalent but with varying densities. If, however, consideration of material composition is important, such as a metal implant, then different materials can be assigned to the corresponding voxels. This can be done by creating a lookup table for material (air, lung, fat, muscle, water, bone, soft bone, metal) as a function of Hounsfield number and then subdividing each material as a function of density.

Transport

During particle transport, the step size is sampled from the exponential distribution. The exponent in the exponential distribution is related to the mean free path that depends on the particle energy and the material in which the particle travels. For neutral particles (photons or neutrons), the step size is relatively large. For example, the mean free path of a 60Co photon in water is 16 cm. For charged particles (electrons, positrons, protons), the step size is very short due to the Coulomb force. As a result, direct simulation would be very inefficient. To overcome this problem, multiple steps are condensed into a single step, called the condensed-history step (143). Energy deposition due to continuous slowing down is calculated along this step and angular deflection is sampled at the end of the step based on multiple scattering theory.

When transporting a particle, it may cross the boundary of one geometric object to another. When this happens, the original step has to be truncated at the boundary. This is because the next geometric object may have different physical properties from the current one. The remaining step size will have to be adjusted based on the new object and resampled if necessary.

For charged particles, there is continuous energy loss due to ionization and excitation. The energy can be deposited uniformly along the step or at a point randomly selected within the step. For neutral particles, there is no energy deposition during a step. However, if the KERMA (Kinetic Energy Released per unit Mass) approximation is made, then energy can also be deposited using the energy absorption coefficient and the step length, which is an estimate of the photon fluence.

Interaction Types

For radiation therapy dose calculation, we are mostly interested in photons and electrons, so the discussion of interaction types here is limited to these radiation particles only.

For photons, the interaction types are photoelectric, Compton scattering, and pair production. Coherent scattering is relatively unimportant as it involves no energy loss and only small angular deflection. In a photoelectric interaction, the incoming photon collides with an atom and ejects one of the bound electrons (typically K shell). The accompanying fluorescent X rays are low energy photons

and are usually ignored in radiation therapy dose calculations. In a Compton scattering event, the incoming photon knocks off a loosely bound electron, considered as a free electron, from the atom. The photon itself is deflected with a lower energy. This is the dominant event for interaction of megavoltage photons with matter. The angular distribution of the outgoing particle is governed by the Klein– Nishina formula, and the angle of the outgoing particle uniquely defines its energy. In a pair production, the incoming photon is absorbed in the field of the nucleus and a positron–electron pair is produced. For this interaction to occur, the photon energy must be > 1.022 MeV, the sum of the rest mass energies of the positron–electron pair.

For electrons and positrons, the discrete interaction types are bremsstrahlung production, delta-ray production, and positron annihilation. Bremsstrahlung production is caused by the deceleration of charged particles (electrons and positrons) passing by the atomic nuclei. This is the mechanism by which photon beams are produced in a linear accelerator. The bremsstrahlung energy spectrum is continuous with the maximum energy equal to the kinetic energy of the incoming electron. The angular distribution is largely forward. A delta-ray is the secondary electron ejected from the atom resulting from a large energy transfer from the incoming electron or positron. If the incident particle is an electron, then the energy of the delta-ray cannot exceed one-half of the incident electron energy, for by definition, the outgoing electron with the lesser energy is the delta-ray. If the incident particle is a positron, then it can give up all its energy to the delta-ray. Positron annihilation is the process that occurs when a positron and an electron collide. If they are approximately at rest relative to each other, they destroy each other upon contact, and produce two photons of 511 keV each that are emitted in opposite directions. If they are moving at different relative speeds, the energies of the photons emitted will be higher.

APPLICATIONS IN RADIATION THERAPY DOSE CALCULATION

Beam Characteristics

In order to perform dose calculation using the Monte Carlo method, it is necessary to have accurate information about the radiation field incident upon the patient, that is, the phase-space data. This data is difficult to obtain by empirical means, therefore in practice it is obtained by Monte Carlo simulation of the machine head. Figure 1 shows a typical configuration of the machine head for a medical linear accelerator that produces clinical photon beams. The components directly in the beam are the target, the flattening filter, and the monitor chamber. The components that collimate the beam are the primary collimator, and the upper and lower collimating jaws. The phase space data can be collected on two scoring planes above and below the collimating jaws, respectively. For clinical electron beams, the machine head is similar to that of photon beams except that the target is removed, the flattening filter is replaced by a scattering foil system, and an additional applicator is used for further collimation of the electron beam (Fig. 2).

Figure 1. Production of a clinical photon beam (drawing not to scale).

Figure 2. Production of a clinical electron beam (drawing not to scale).

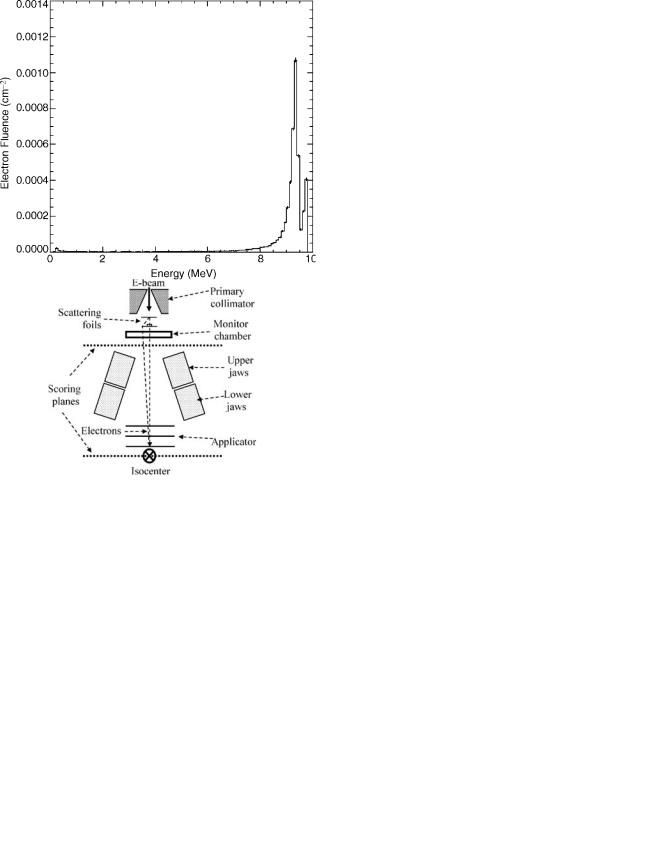
Figure 3 shows the energy spectra of a 15 MV photon beam. Note that the low energy photons have been filtered out by the flattening filter. Moreover, the spectrum near the center of the beam, say, within 3 cm of the central axis, is harder than that away from the axis, say, 10–15 cm from

Figure 4. The energy spectrum of a clinical 9 MeV electron beam.

the center. The reason is that the flattening filter is thicker in the middle, thus absorbing more low energy photons. Figure 4 shows the energy spectrum of a clinical 9 MeV electron beam. It is clear there are two peaks corresponding to the thin part and the thick part of the scattering foil system. Figure 5 shows the angular distribution of the electrons at the isocenter plane ( 100 cm from the entrance to the primary collimator). Due to the significant scattering of electrons in the scattering foils as well as in the air space above the isocenter, the angular spread is diffused and approximates a normal distribution.

This information about beam characteristics such as the energy and angular distributions is difficult to measure, but can be calculated by Monte Carlo with relative ease.

Many modern dose calculation algorithms other than Monte Carlo are quite accurate for megavoltage (60Co– 20 MV) external photon beam radiation therapy for sites that are composed of soft tissue (density 1 g mL 1) and bone (brain, pelvis, limbs) (144). However, these algorithms are less accurate when electronic equilibrium is lost due to more severe tissue inhomogeneities. This may be a clinical concern in the lung, where soft tissue tumors are surrounded by low density ( 0.2–0.3 g mL 1) lung and in the head and neck (H&N) due to the presence of air cavities. Although Monte Carlo is currently impractical for routine clinical use, Monte Carlo calculations based on patient CT scans and inhomogeneous phantoms provide clinically valuable information, especially when combined with high resolution phantom measurements (film and/or TLD). For a summary of the status of the field (145).

Lung Cancer

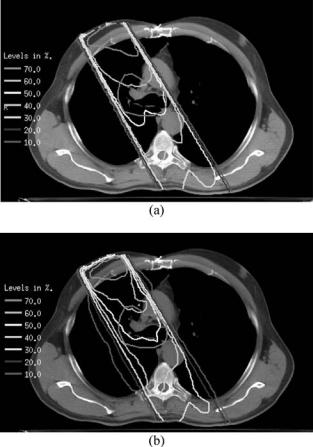
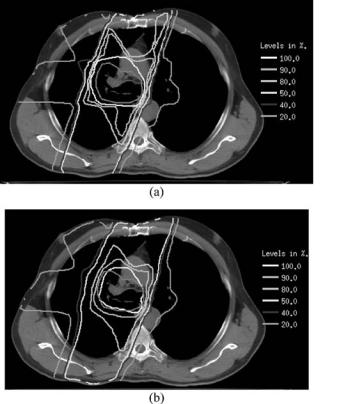
Since lung has lower electron density than soft tissue, there is reduced attenuation of the primary photons of a beam traversing lung compared with the same path length in soft tissue. Most inhomogeneity correction algorithms can account for this effect (144). However, other, more subtle effects are described with reasonable approximation only by superposition-convolution algorithms (146,147) and most accurately by Monte Carlo. The cause of these effects is the long range of the secondary electrons in lung compared to soft tissue (the range is approximately inversely proportional to the ratio of lung to soft tissue density). Energy is thus transported outside the beam’s geometric edge, resulting in a broader beam penumbra and reduced dose within the beam. Also, especially for a small soft tissue target embedded in a very low density medium and irradiated with a tight, high energy beam, there is a builddown (low dose region) at the entrance surface and sides of the target. All these effects are more pronounced for higher energy beams and lower density lungs (longer electron ranges) and smaller fields. The clinical concern is that treatment plans developed with algorithms that do not account for these effects can result in target underdose and/or overdose to normal tissues in penumbral regions. Figure 6 shows characteristic differences between the dose distribution of a single 6 MV photon beam predicted by a measurement-based pencil beam calculation that accounts only for changes in primary attenuation and that predicted by a Monte Carlo calculation. Lung radiation treatments usually consist of two or more beams, incident on the tumor in a cross-fire technique. Figure 7 shows that even in this patient’s full four-field plan, these characteristic differences between the Monte Carlo and pencil beam calculations persist.

The degree to which the target underdose and broader penumbra in lung may compromise complications-free tumor control has been addressed in several studies (24,33,34,148–155). References 148–151 used measurements only to investigate penumbra broadening and build-down effects. A recent study (154) combined film dosimetry and EGSnrc and DOSXYZnrc Monte Carlo calculations to study the dose distribution in a 2 2 2 cm

Figure 6. Dose distribution of a single 6 MV photon beam (a) predicted by a measurement-based pencil beam calculation that accounts only for changes in primary attenuation and (b) that predicted by a Monte Carlo calculation. The red contour indicates the target. Please use online version for color figure.

acrylic ( tissue density) cube embedded in cork, simulating a small lesion in lung irradiated with a single and with parallel opposed photon beams from 4 to 18 MV. The parallel opposed geometry is a common field arrangement for treatment of lung tumors. Cork density, field size, and depth of the lesion in cork were varied. For the entire target cube to receive at least 95% of the dose to its center required field edges of the parallel opposed fields to be at least 2 cm from the cube even for the most favorable case (4 MV photons).

Other recent studies from different institutions have compared more complex treatment plans designed on anatomical phantoms or patient CT image sets and calculated with Monte Carlo versus the local treatment planning system calculation algorithm (24,34,152,153,155). In these studies, as in routine clinical practice, the beam is shaped to cover the planning target volume (PTV), which is larger than the grossly visible tumor gross target volume (GTV). The margin is intended to account for microscopic disease, setup error and breathing motion. Based on these studies, it is expected that (a) Results depend on the treatment planning system algorithm (34,153,155); (b) For the same planning system, results are patient (phantom geometry)

Figure 7. Dose distributions of a four-field plan in the lung. Figure (a) and (b) show dose distributions on a transverse plane predicted by a measurement-based pencil beam calculation and by a Monte Carlo calculation, respectively. The red contour indicates the target. Please see online version for color figure.

dependent as well as dependent on beam energy (24,33,34,153,155); (c) Changes quoted depend on the dosimetric coverage factor being evaluated. Mean target dose and dose encompassing 95% of the target volume are relatively insensitive indices; minimum dose (a single point) and dose-volume points on rapidly changing portions of the dose-volume histogram are more sensitive; (d) The PTV is usually underdosed relative to expectations from the treatment planning system. The degree of underdose varies from 1 to 20%, for 6 MV photons, depending on the dosimetric coverage factor, the lung density and the tumor location. For most of the cases reported, the underdosage is < 10%; (e) The planning system results for coverage of the GTV are more similar to Monte Carlo, as is expected because the margin results in a larger distance from geometric beam edge to the GTV border than to the PTV border; (f) The greatest differences are for tumors surrounded by very low density lungs (33,34); (g) There are greater differences for high (e.g., 15 MV) than low (6 MV) energy beams (153); (h) Normal organ doses (primarily lung and spinal cord) are only slightly affected.

Head and Neck Cancer

H&N cancer radiation therapy usually includes photon irradiation with low megavoltage beams (60Co—6 MV). Target tissue often borders on naturally occurring or sur-

gical air cavities. Experiments demonstrate that builddown accompanying the loss of electronic equilibrium in air cavities in tissue-equivalent phantoms can cause up to a 25% underdose within the first millimeter of tissue (156–159), with particularly pronounced effects for small ( 5 5 cm2) fields, such as are used for treatment of larynx cancer. Whether this impacts on local control of larynx cancers treated with 6 MV beams versus 60Co has not been resolved (160). The penumbra broadening and loss of dose within the beam that are noted in lung also occur in air cavities but the small size of these cavities, compared to the size of a lung, prevent these effects from posing a serious clinical problem.

Monte Carlo calculations compared well with parallel plate ion chamber measurements for single field and parallel opposed field irradiation (4, 6, and 8 MV photons) of a 4 4 4 cm3 cavity centered in a 30 30 16 cm3 phantom (161) though neither method had the spatial resolution to probe the build-down region in detail. A few studies have compared dose distributions on patient CT image sets for clinical beam arrangements as calculated with the local planning system and with Monte Carlo calculations for the same beams (31,33,162). Differences between the two calculation methods are more noticeable for individual beams than when all the beams (from two to seven, depending on the plan) are combined for the overall treatment plan. Monte Carlo predicts inferior target coverage compared to the planning system, but the differences, which depend on dosimetric index and tumor geometry, are less than in lung. Spinal cord maximum dose differences of < 1 Gy were reported in (31) (with the Monte Carlo calculation sometimes higher, sometimes lower) and 3 Gy higher as calculated by Monte Carlo in (162).

DISCUSSION

For treatment planning dose calculations, Monte Carlo is potentially the most accurate method. Monte Carlo dose calculation for electron beams has recently become available on a commercial treatment planning system (48). For photon beams, however, it has not been practical for routine clinical use due to its long running time. To improve the computation efficiency, there are variance reduction techniques available. The most common techniques are splitting and Russian roulette (136). In splitting, a particle isartificiallysplitintomultipleparticlesinimportantregions to produce more histories. In Russian roulette, particles are artificially terminated in relatively unimportant regions to reduce the number of histories. In both techniques, the particle weight, of course, needs to be adjusted to reflect the artificial increase or decrease of histories.

In addition to dose calculation, perhaps a more important application of Monte Carlo is to provide information that cannot be easily obtained by measurement. For example, in the simulation of the machine head, the phase-space data provide information on the primary and scattered radiation from various components in the machine head. These data provide important information in understanding the beam characteristics and may be used for other dose calculation methods.

BIBLIOGRAPHY

1.Andreo P. Monte Carlo techniques in medical radiation physics. Phys Med Biol 1991;36(7):861–920.

2.Mohan R, Chui C, Lidofsky L. Energy and angular distributions of photons from medical linear accelerators. Med Phys 1985;12(5):592–597.

3.Han K, et al. Monte Carlo simulation of a cobalt-60 beam. Med Phys 1987;14(3):414–419.

4.Chaney EL, Cullip TJ, Gabriel TA. A Monte Carlo study of accelerator head scatter. Med Phys 1994;21(9):1383–1390.

5.Lovelock DM, Chui CS, Mohan R. A Monte Carlo model of photon beams used in radiation therapy. Med Phys 1995 ;22(9):1387–1394.

6.Lee PC. Monte Carlo simulations of the differential beam hardening effect of a flattening filter on a therapeutic X-ray beam. Med Phys 1997;24(9):1485–1489.

7.Bhat M, et al. Off-axis X-ray spectra: a comparison of Monte Carlo simulated and computed X-ray spectra with measured spectra. Med Phys 1999;26(2):303–309.

8.Libby B, Siebers J, Mohan R. Validation of Monte Carlo generated phase-space descriptions of medical linear accelerators. Med Phys 1999;26(8):1476–1483.

9.Ma CM, Jiang SB. Monte Carlo modelling of electron beams from medical accelerators. Phys Med Biol 1999;44(12):R157– R189.

10.Siebers JV, et al. Comparison of EGS4 and MCNP4b Monte Carlo codes for generation of photon phase space distributions for a Varian 2100C. Phys Med Biol 1999; 44(12):3009–3026.

11.van der Zee W, Welleweerd J. Calculating photon beam characteristics with Monte Carlo techniques. Med Phys 1999;26(9): 1883–1892.

12.Deng J, et al. Photon beam characterization and modelling for Monte Carlo treatment planning. Phys Med Biol 2000;45(2): 411–427.

13.Bieda MR, Antolak JA, Hogstrom KR. The effect of scattering foil parameters on electron-beam Monte Carlo calculations. Med Phys 2001;28(12):2527–2534.

14.Antolak JA, Bieda MR, Hogstrom KR. Using Monte Carlo methods to commission electron beams: a feasibility study. Med Phys 2002;29(5):771–786.

15.Ding GX. Energy spectra, angular spread, fluence profiles and dose distributions of 6 and 18 MV photon beams: results of monte carlo simulations for a varian 2100EX accelerator. Phys Med Biol 2002;47(7):1025–1046.

16.Sheikh-Bagheri D, Rogers DW. Monte Carlo calculation of nine megavoltage photon beam spectra using the BEAM code. Med Phys 2002;29(3):391–402.

17.van der Zee W, Welleweerd J. A Monte Carlo study on internal wedges using BEAM. Med Phys 2002;29(5):876–885.

18.Ding GX. Using Monte Carlo simulations to commission photon beam output factors–a feasibility study. Phys Med Biol 2003;48(23):3865–3874.

19.Van de Walle J, et al. Monte Carlo model of the Elekta SLiplus accelerator: validation of a new MLC component module in BEAM for a 6 MV beam. Phys Med Biol 2003; 48(3):371–385.

20.Verhaegen F, Seuntjens J. Monte Carlo modelling of external radiotherapy photon beams. Phys Med Biol 2003;48(21):R107–R164.

21.Fix MK, et al. Monte Carlo source model for photon beam radiotherapy: photon source characteristics. Med Phys 2004; 31(11):3106–3121.

22.Pena J, et al. Commissioning of a medical accelerator photon beam Monte Carlo simulation using wide-field profiles. Phys Med Biol 2004;49(21):4929–4942.

23.DeMarco JJ, Solberg TD, Smathers JB. A CT-based Monte Carlo simulation tool for dosimetry planning and analysis. Med Phys 1998;25(1):1–11.

24.Wang L, Chui CS, Lovelock M. A patient-specific Monte Carlo dose-calculation method for photon beams. Med Phys 1998;25(6):867–878.

25.Jeraj R, Keall P. Monte Carlo-based inverse treatment planning. Phys Med Biol 1999;44(8):1885–1896.

26.Laub W, et al. Monte Carlo dose computation for IMRT optimization. Phys Med Biol 2000;45(7):1741–1754.

27.Lewis RD, et al. Use of Monte Carlo computation in benchmarking radiotherapy treatment planning system algorithms. Phys Med Biol 2000;45(7):1755–1764.

28.Keall PJ, et al. Monte Carlo dose calculations for dynamic IMRT treatments. Phys Med Biol 2001;46(4):929–941.

29.Li XA, et al. Monte Carlo dose verification for intensity-modu- lated arc therapy. Phys Med Biol 2001;46(9):2269–2282.

30.Shih R, Lj XA, Hsu WL. Dosimetric characteristics of dynamic wedged fields: a Monte Carlo study. Phys Med Biol 2001;46(12):N281–N292.

31.Wang L, Yorke E, Chui CS. Monte Carlo evaluation of tissue inhomogeneity effects in the treatment of the head and neck. Int J Radiat Oncol Biol Phys 2001;50(5):1339–1349.

32.Ma CM, et al. A Monte Carlo dose calculation tool for radiotherapy treatment planning. Phys Med Biol 2002;47(10): 1671–1689.

33.Wang L, Yorke E, Chui CS. Monte Carlo evaluation of 6 MV intensity modulated radiotherapy plans for head and neck and lung treatments. Med Phys 2002;29(11):2705–2717.

34.Yorke ED, et al. Evaluation of deep inspiration breath-hold lung treatment plans with Monte Carlo dose calculation. Int J Radiat Oncol Biol Phys 2002;53(4):1058–1070.

35.Leal A, et al. Routine IMRT verification by means of an automated Monte Carlo simulation system. Int J Radiat Oncol Biol Phys 2003;56(1):58–68.

36.Wieslander E, Knoos T. Dose perturbation in the presence of metallic implants: treatment planning system versus Monte Carlo simulations. Phys Med Biol 2003;48(20):3295–3305.

37.Heath E, Seuntjens J, Sheikh-Bagheri D. Dosimetric evaluation of the clinical implementation of the first commercial IMRT Monte Carlo treatment planning system at 6 MV. Med Phys 2004;31(10):2771–2779.

38.Yang J, et al. Modelling of electron contamination in clinical photon beams for Monte Carlo dose calculation. Phys Med Biol 2004;49(12):2657–2673.

39.Kawrakow I, Fippel M, Friedrich K. 3D electron dose calculation using a Voxel based Monte Carlo algorithm (VMC). Med Phys 1996;23(4):445–457.

40.Keall PJ, Hoban PW. Super-Monte Carlo: a 3-D electron beam dose calculation algorithm. Med Phys 1996;23(12): 2023– 2034.

41.Scora D, Faddegon BA. Monte Carlo based phase-space evolution for electron dose calculation. Med Phys 1997;24(2): 177– 187.

42.Jiang SB, Kapur A, Ma CM. Electron beam modeling and commissioning for Monte Carlo treatment planning. Med Phys 2000;27(1):180–191.

43.Kawrakow I. Accurate condensed history Monte Carlo simulation of electron transport. I. EGSnrc, the new EGS4 version. Med Phys 2000;27(3):485–498.

44.Lee MC, et al. Monte Carlo based treatment planning for modulated electron beam radiation therapy. Phys Med Biol 2001;46(8):2177–2199.

45.Bjork P, Knoos T, Nilsson P. Influence of initial electron beam characteristics on monte carlo calculated absorbed dose distributions for linear accelerator electron beams. Phys Med Biol 2002;47(22):4019–4041.

46.Deng J, Lee MC, Ma CM. A Monte Carlo investigation of fluence profiles collimated by an electron specific MLC during beam delivery for modulated electron radiation therapy. Med Phys 2002;29(11):2472–2483.

47.Doucet R, et al. Comparison of measured and Monte Carlo calculated dose distributions in inhomogeneous phantoms in clinical electron beams. Phys Med Biol 2003;48(15):2339– 2354.

48.Cygler JE, et al. Evaluation of the first commercial Monte Carlo dose calculation engine for electron beam treatment planning. Med Phys 2004;31(1):142–153.

49.Coleman J, et al. A comparison of Monte Carlo and Fermi- Eyges-Hogstrom estimates of heart and lung dose from breast electron boost treatment. Int J Radiat Oncol Biol Phys 2005;61(2):621–628.

50.Carlsson AK, Andreo P, Brahme A. Monte Carlo and analytical calculation of proton pencil beams for computerized treatment plan optimization. Phys Med Biol 1997;42(6): 1033–1053.

51.Paganetti H. Monte Carlo method to study the proton fluence for treatment planning. Med Phys 1998;25(12):2370–2375.

52.Fippel M, Soukup M. A Monte Carlo dose calculation algorithm for proton therapy. Med Phys 2004;31(8):2263–2273.

53.Jiang H, Paganetti H. Adaptation of GEANT4 to Monte Carlo dose calculations based on CT data. Med Phys 2004;31(10): 2811–2818.

54.Paganetti H. Four-dimensional Monte Carlo simulation of time-dependent geometries. Phys Med Biol 2004;49(6):N75– N81.

55.Williamson JF, Morin RL, Khan FM. Monte Carlo evaluation of the Sievert integral for brachytherapy dosimetry. Phys Med Biol 1983;28(9):1021–1032.

56.Burns GS, Raeside DE. Monte Carlo simulation of the dose distribution around 125I seeds. Med Phys 1987;14(3):420– 424.

57.Williamson JF. Monte Carlo evaluation of specific dose constants in water for 125I seeds. Med PhysM 1988;15(5):686– 694.

58.Angelopoulos A, et al. Accurate Monte Carlo calculations of the combined attenuation and build-up factors, for energies (20– 1500 keV) and distances (0–10 cm) relevant in brachytherapy. Phys Med Biol 1991;36(6):763–778.

59.Williamson JF, Li Z. Monte Carlo aided dosimetry of the microselectron pulsed and high dose-rate 192Ir sources. Med Phys 1995;22(6):809–819.

60.Weaver K, et al. A source model for efficient brachytherapy computations with Monte Carlo. Med Phys 1996;23(12): 2079– 2084.

61.Cheung YC, et al. The dose distribution close to an 192Ir wire source: EGS4 Monte Carlo calculations. Phys Med Biol 1997;42(2):401–406.

62.Baltas D, et al. Application of the Monte Carlo integration (MCI) method for calculation of the anisotropy of 192Ir brachytherapy sources. Phys Med Biol 1998;43(6):1783–1801.

63.Daskalov GM, Loffler E, Williamson JF. Monte Carlo-aided dosimetry of a new high dose-rate brachytherapy source. Med Phys 1998;25(11):2200–2208.

64.Mainegra E, Capote R, Lopez E. Dose rate constants for 125I, 103Pd, 192Ir and 169Yb brachytherapy sources: an EGS4 Monte Carlo study. Phys Med Biol 1998;43(6):1557– 1566.

65.Wang R, Sloboda RS. Monte Carlo dosimetry of the VariSource high dose rate 192Ir source. Med Phys 1998;25(4): 415–423.

66.Karaiskos P, et al. A Monte Carlo investigation of the dosimetric characteristics of the VariSource 192Ir high dose rate brachytherapy source. Med Phys 1999;26(8):1498–1502.

67.Reynaert N, et al. Monte Carlo calculations of dose distributions around 32P and 198Au stents for intravascular brachytherapy. Med Phys 1999;26(8):1484–1491.

68.Casal E, et al. Monte Carlo calculations of dose rate distributions around the Amersham CDCS-M-type 137Cs source. Med Phys 2000;27(1):132–140.

69.Hedtjarn H, Carlsson GA, Williamson JF. Monte Carlo-aided dosimetry of the Symmetra model I25.S06 125I, interstitial brachytherapy seed. Med Phys 2000;27(5):1076–1085.

70.Li Z, Palta JR, Fan JJ. Monte Carlo calculations and experimental measurements of dosimetry parameters of a new 103Pd source. Med Phys 2000;27(5):1108–1112.

71.Mainegra E, Capote R, Lopez E. Radial dose functions for 103Pd, 125I, 169Yb and 192Ir brachytherapy sources: an EGS4 Monte Carlo study. Phys Med Biol 2000;45(3):703–717.

72.Mainegra E, Capote R, Lopez E. Anisotropy functions for 169Yb brachytherapy seed models 5, 8 and X1267. An EGS4 Monte Carlo study. Phys Med Biol 2000;45(12):3693–3705.

73.Williamson JF. Monte Carlo modeling of the transverse-axis dose distribution of the model 200 103Pd interstitial brachytherapy source. Med Phys 2000;27(4):643–654.

74.Ballester F, et al. Technical note: Monte-Carlo dosimetry of the HDR 12i and Plus 192Ir sources. Med Phys 2001;28(12): 2586–2591.

75.Capote R, Mainegra E, Lopez E. Anisotropy function for 192Ir low-dose-rate brachytherapy sources: an EGS4 Monte Carlo study. Phys Med Biol 2001;46(5):1487–1499.

76.Rivard MJ. Monte Carlo calculations of AAPM Task Group Report No. 43 dosimetry parameters for the MED3631-A/ M125I source. Med Phys 2001;28(4):629–637.

77.Chan GH, Prestwich WV. Monte carlo investigation of the dosimetric properties of the new 103Pd BrachySeedPd-103 Model Pd-1 source. Med Phys 2002;29(9):1984–1990.

78.Hedtjarn H, Carlsson GA, Williamson JF. Accelerated Monte Carlo based dose calculations for brachytherapy planning using correlated sampling. Phys Med Biol 2002;47(3):351–376.

79.Ibbott GS, Meigooni AS, Gearheart DM. Monte Carlo determination of dose rate constant. Med Phys 2002;29(7):1637– 1638.

80.Bohm TD, DeLuca Jr PM, DeWerd LA. Brachytherapy dosimetry of 125I and 103Pd sources using an updated cross section library for the MCNP Monte Carlo transport code. Med Phys 2003;30(4):701–711.

81.Medich DC, Munro JJ. 3rd, Monte Carlo calculated TG-43 dosimetry parameters for the SeedLink 125Iodine brachytherapy system. Med Phys 2003;30(9):2503–2508.

82.Anagnostopoulos G, et al. The effect of patient inhomogeneities in oesophageal 192Ir HDR brachytherapy: a Monte Carlo and analytical dosimetry study. Phys Med Biol 2004; 49(12):2675–2685.

83.Ballester F, et al. Monte carlo dosimetric study of best industries and Alpha Omega Ir-192 brachytherapy seeds. Med Phys 2004;31(12):3298–3305.

84.Lymperopoulou G, et al. A monte carlo dosimetry study of vaginal 192Ir brachytherapy applications with a shielded cylindrical applicator set. Med Phys 2004;31(11):3080–3086.

85.Reniers B, Verhaegen F, Vynckier S. The radial dose function of low-energy brachytherapy seeds in different solid phantoms: comparison between calculations with the EGSnrc and MCNP4C Monte Carlo codes and measurements. Phys Med Biol 2004;49(8):1569–1582.

86.Perez-Calatayud J, et al. Monte carlo and experimental derivation of TG43 dosimetric parameters for CSM-type Cs-137 sources. Med Phys 2005;32(1):28–36.

87.Furhang EE, Chui CS, Sgouros G. A Monte Carlo approach to patient-specific dosimetry. Med Phys 1996;23(9):1523– 1529.

88.Tagesson M, Ljungberg M, Strand SE. A Monte-Carlo program converting activity distributions to absorbed dose distributions in a radionuclide treatment planning system. Acta Oncol 1996;35(3):367–372.

89.Liu A, et al. Monte Carlo-assisted voxel source kernel method (MAVSK) for internal beta dosimetry. Nucl Med Biol 1998; 25(4):423–433.

90.Clairand I, et al. DOSE3D: EGS4 Monte Carlo code-based software for internal radionuclide dosimetry. J Nucl Med 1999;40(9):1517–1523.

91.Zaidi H. Relevance of accurate Monte Carlo modeling in nuclear medical imaging. Med Phys 1999;26(4):574–608.

92.Chao TC, Xu XG. Specific absorbed fractions from the imagebased VIP-Man body model and EGS4-VLSI Monte Carlo code: internal electron emitters. Phys Med Biol 2001;46(4): 901–927.

93.Kvinnsland Y, Skretting A, Bruland OS. Radionuclide therapy with bone-seeking compounds: Monte Carlo calculations of dose-volume histograms for bone marrow in trabecular bone. Phys Med Biol 2001;46(4):1149–1161.

94.Yoriyaz H, Stabin MG, dos Santos A. Monte Carlo MCNP-4B- based absorbed dose distribution estimates for patient-specific dosimetry. J Nucl Med 2001;42(4):662–669.

95.Ljungberg M, et al. A 3-dimensional absorbed dose calculation method based on quantitative SPECT for radionuclide therapy: evaluation for (131)I using monte carlo simulation. J Nucl Med 2002;43(8):1101–1109.

96.Kinase S, et al. Evaluation of specific absorbed fractions in voxel phantoms using Monte Carlo simulation. Radiat Prot Dosimet 2003;105(1–4):557–563.

97.Wolf I, et al. Determination of Individual S-Values for (131)I Using Segmented CT Data and the EGS4 Monte Carlo Code. Cancer Biother Radiopharm 2005;20(1):98–102.

98.Chan HP, Doi K. Radiation dose in diagnostic radiology: Monte Carlo simulation studies. Med Phys 1984;11(4):480–490.

99.Dance DR, Day GJ. The computation of scatter in mammography by Monte Carlo methods. Phys Med Biol 1984;29(3): 237–247.

100.Kulkarni RN, Supe SJ. Radiation dose to the breast during mammography: a comprehensive, realistic Monte Carlo calculation. Phys Med Biol 1984;29(10):1257–1264.

101.Kulkarni RN, Supe SJ. Monte Carlo calculations of mammographic X-ray spectra. Phys Med Biol 1984;29(2):185–190.

102.Boone JM, Seibert JA. Monte Carlo simulation of the scattered radiation distribution in diagnostic radiology. Med Phys 1988;15(5):713–720.

103.Papin PJ, Rielly PS. Monte Carlo simulation of diagnostic X- ray scatter. Med Phys 1988;15(6):909–914.

104.Gao W, Raeside DE. Orthovoltage radiation therapy treatment planning using Monte Carlo simulation: treatment of neuroendocrine carcinoma of the maxillary sinus. Phys Med Biol 1997;42(12):2421–2433.

105.Verhaegen F, et al. Monte Carlo modelling of radiotherapy kV X-ray units. Phys Med Biol 1999;44(7):1767–1789.

106.Boone JM, Cooper 3rd VN. Scatter/primary in mammography: Monte Carlo validation. Med Phys 2000;27(8):1818–1831.

107.Boone JM, Buonocore MH, Cooper 3rd VN. Monte Carlo validation in diagnostic radiological imaging. Med Phys 2000;27(6):1294–1304.

108.Ng KP, Kwok CS, Tang FH. Monte Carlo simulation of X-ray spectra in mammography. Phys Med Biol 2000;45(5):1309–1318.

109.Peplow DE, Verghese K. Digital mammography image simulation using Monte Carlo. Med Phys 2000;27(3):568–579.

110.Kramer R, et al. Backscatter factors for mammography calculated with Monte Carlo methods. Phys Med Biol 2001; 46(3):771–781.

111.Ay MR, et al. Monte carlo simulation of X-ray spectra in diagnostic radiology and mammography using MCNP4C. Phys Med Biol 2004;49(21):4897–4917.

112.Andreo P, Nahum A, Brahme A. Chamber-dependent wall correction factors in dosimetry. Phys Med Biol 1986;31(11): 1189–1199.

113.Rogers DW. Calibration of parallel-plate chambers: resolution of several problems by using Monte Carlo calculations. Med Phys 1992;19(4):889–899.

114.Ma CM, Nahum AE. Calculations of ion chamber displacement effect corrections for medium-energy X-ray dosimetry. Phys Med Biol 1995;40(1):45–62.

115.Ma CM, Nahum AE. Monte Carlo calculated stem effect correction for NE2561 and NE2571 chambers in mediumenergy X-ray beams. Phys Med Biol 1995;40(1):63–72.

116.Mobit PN, Nahum AE, Mayles P. An EGS4 Monte Carlo examination of general cavity theory. Phys Med Biol 1997; 42(7):1319–1334.

117.Ferreira IH, et al. Perturbation corrections for flat and thimble-type cylindrical standard ionization chambers for 60Co gamma rays: Monte Carlo calculations. Phys Med Biol 1998;43(10):2721–2727.

118.Ferreira IH, et al. Monte Carlo calculations of the ionization chamber wall correction factors for 192Ir and 60Co gamma rays and 250 kV X-rays for use in calibration of 192Ir HDR brachytherapy sources. Phys Med Biol 1999;44(8):1897– 1904.

119.Borg J, et al. Monte Carlo study of correction factors for Spencer-Attix cavity theory at photon energies at or above 100 keV. Med Phys 2000;27(8):1804–1813.

120.Seuntjens JP, et al. Absorbed-dose beam quality conversion factors for cylindrical chambers in high energy photon beams. Med Phys 2000;27(12):2763–2779.

121.Mazurier J, et al. Calculation of perturbation correction factors for some reference dosimeters in high-energy photon beams with the Monte Carlo code PENELOPE. Phys Med Biol 2001;46(6):1707–1717.

122.Fu Y, Luo Z. Application of Monte Carlo simulation to cavity theory based on the virtual electron source concept. Phys Med Biol 2002;47(17):3263–3274.

123.Mainegra-Hing E, Kawrakow I, Rogers DW. Calculations for plane-parallel ion chambers in 60Co beams using the EGSnrc Monte Carlo code. Med Phys 2003;30(2):179–189.

124.Piermattei A, et al. The wall correction factor for a spherical ionization chamber used in brachytherapy source calibration. Phys Med Biol 2003;48(24):4091–4103.

125.Rogers DW, Kawrakow I. Monte Carlo calculated correction factors for primary standards of air kerma. Med Phys 2003;30(4):521–532.

126.Siegbahn EA, et al. Calculations of electron fluence correction factors using the Monte Carlo code PENELOPE. Phys Med Biol 2003;48(10):1263–1275.

127.Capote R, et al. An EGSnrc Monte Carlo study of the microionization chamber for reference dosimetry of narrow irregular IMRT beamlets. Med Phys 2004;31(9):2416–2422.

128.McCaffrey JP, et al. Evidence for using Monte Carlo calculated wall attenuation and scatter correction factors for three styles of graphite-walled ion chamber. Phys Med Biol 2004;49(12):2491–2501.

129.Sempau J, et al. Electron beam quality correction factors for plane-parallel ionization chambers: Monte Carlo calculations using the PENELOPE system. Phys Med Biol 2004;49(18): 4427–4444.

130.Nelson WR, Hirayama H, Rogers DWO. The EGS4 Code System. 1985; Stanford Linear Accelerator Center.

131.GEANT team, GEANT version 315. 1992, CERN-data handling division, report DD/EE/84-1 revision.