fizika

6.8.2. Виды волн

Вид волн определяется источником колебания. Если источник колебаний очень мал (точечный источник), то волны от него радиально расходятся во все стороны, как это показано на рис. 6.17.

Радиальная прямая, проведенная от точечного источника, вдоль которой распространяется волна, называется лучом. Волновая поверхность от точечного источника имеет форму сферы. Такая волна называется

сферической.

В изотропной среде (т. е. среде, свойства которой не зависят от направления), волновой вектор перпендикулярен волновой поверхности.

Если источник колебаний — протяженная плоскость, то волновая поверхность имеет форму плоскости. Такая волна называется плоской. В плоской волне все лучи, вдоль которых она распространяется, параллельны друг другу, например, параллельны оси х (рис. 6.18).

В однородной среде колебание вдоль всех параллельных лучей распространяется с одинаковой фазовой скоростью u.

Кроме плоских и сферических волн можно выделить также волны цилиндрические, у которых вол-

новые поверхности — концентрические цилиндры. Такие волны возбуждаются нитевидными или щелевыми источниками.

Среди волн разнообразной физической природы выделяют помимо упругих волн и волн на поверхности жидкости, электромагнитные и плазменные волны. Особенно большое значение в природе и технике играют электромагнитные волны.

6.8.3. Уравнение плоской гармонической волны

Уравнением плоской гармонической волны называется периодическая функция ξ = ξ(x, C, z,t) , позволяющая найти смещение от положения равновесия частицы волнового поля в любой момент времени.

РассмотримG случай, когда плоская волна распространяется со скоростью u в однородной изотропной среде в направлении оси х (рис. 6.19). Смещение частицы зависит от времени t и координаты х той волновой поверхности, которой эта частица принадлежит

ξ= ξ(x,t) .

Внашем примере Gлучом является ось х. Пусть волна распространяется со скоростью u . Если волна гармоническая, то в каждой точке пространства частица совершает гармоническое колебание.

Пусть колебания частиц, принадлежащих волновой поверхности

скоординатой х = 0, описываются уравнением

Колебания частиц с координатой х начнутся позже, так как требуется время t для того, чтобы волна прошла расстояние х от колеблющейся точки до источника колебаний. Время прохождения волной этого расстояния равно

τ = ux .

Следовательно, колебания частиц с координатой х будут отставать по времени от колебаний частиц с координатой х = 0 на τ:

фаза колебаний волны в произвольной точке с координатой х, k — модуль волнового вектора (см. 6.50). Волновой вектор указывает на направление распространения волны.

Равенство (6.52) называется уравнением плоской гармонической волны.

Фазы колебаний в разных точках среды отличаются. Вычислим разность фаз в двух точках среды, определяемых координатами х1 и

Уравнение (6.52) называют уравнением прямой волны. Уравнение плоской гармонической волны, распространяющейся

в направлении, противоположном направлению оси х, имеет вид

ξ(x,t) = Acos(ωt + kx) .

Это уравнение обратной волны.

Уравнение плоской гармонической волны, распространяющейся

rG — радиус-вектор, определяющий положение рассматриваемой частицы.

Более сложные волны можно представить в виде суперпозиции гармонической волны.

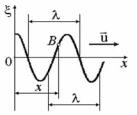
Если в (6.53) зафиксировать t, то зависимость волновой функции от х дает как бы моментальную фотографию волны (застывшую синусоиду), т. е. значение амплитуды колебаний каждой точки в данный момент времени. Пространственный период ее, т. е. расстояние между точками, в которых совпадают значения ξ и значение ее производной по координате, называется длиной волны и обозначается буквой λ (рис. 6.19).

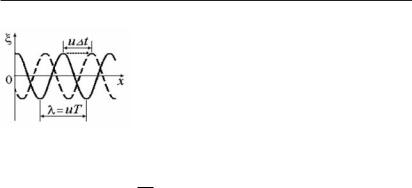
384 Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ

функции ξ на рис. 6.20) смещается за это время на расстояние u t.

Длина волны λ = uT = 2kπ .

Зависимость ξ = ξ(x,t) можно найти, решая волновое уравнение. Волновое уравнение — дифференциальное уравнение с частными производными 2-го порядка от смещения и времени, описывающее процесс распространения возмущений в упругой среде. Оно связывает вторые частные производные от смещения по координатам со вторыми частными производными от смещения по времени. Если продифференцировать (6.52) дважды по времени, затем дважды по координате, то получим

уравнение плоской гармонической волны, распространяющейся в направлении оси х:

задачи, связанные с распространением волны. Например, можно получить скорость распространения волны в натянутой струне.

Если волна распространяется в произвольном направлении, то в левой части волнового уравнения появляются слагаемые, содержащие вторые частные производные по у и z

∂2ξ + ∂2ξ + ∂2ξ = 1 ∂2ξ

∂x2 ∂y2 ∂z2 u2 ∂t2 .

Решением этого уравнения в зависимости от дополнительных условий могут быть уравнения ξ = ξ(x, y, z,t) плоской, сферической, цилиндрической или других волн.

Скорость волны зависит от свойств среды, в которой волна распространяется (в частности, от плотности ρ и коэффициентов, характеризующих упругость среды).

Приведем без доказательства примеры формул для расчета скорости распространения волны в разных средах, которые могут быть полезны при решении конкретных задач.

1. В растянутой струне скорость распространения поперечной волны зависит от силы натяжения струны FT и от массы, приходящейся

2. Скорость распространения продольной волны в твердом тонком

где Е — модуль Юнга (модуль продольной упругости материала). 3. Скорость распространения поперечной волны в твердом теле

u = Gρ ,

где G — модуль сдвига среды.

4. Скорость распространения звуковой волны в идеальном газе

где k — показатель адиабаты, Т — температура, R — универсальная газовая постоянная, μ — молярная масса газа.

6.8.4. Интерференция волн

Если в среде имеется не один, а несколько источников волн, то на каждую точку среды воздействуют одновременно несколько волновых движений. Если волны имеют одинаковую циклическую частоту и накладываются друг на друга, то наблюдается явление интерференции.

Интерференция — наложение волн, при котором колебания, обусловленные этими волнами, в одних местах усиливают друг друга, а в других — ослабляют.

Интерферировать могут лишь когерентные волны.

Две волны называются когерентными, если разность их фаз в каждой точке волнового поля остается неизменной.

Источники таких волн называются когерентными. Рассмотрим наложение волн от двух когерентных источников.

Пусть из двух когерентных источников, расположенных на некотором расстоянии друг от друга, генерируют сферические поперечные гармонические волны в одинаковых фазах. В произвольной точке, отстоящей от источников на расстояния r1 и r2, волны, создаваемые этими источниками, будут сдвинуты по фазе из-за того, что r1 ≠ r2 . Результирующее колебание в заданной точке равно сумме составляющих колебаний

ξ(r,t) = ξ(r1 ,t) + ξ(r2 ,t) = A1 cos(ωt − kr1 ) + A2 cos(ωt − kr2 ) , где А1 и А2 — амплитуды волн, k — волновое число.

Разность фаз волн в заданной точке равна

ϕ2 − ϕ1 = (ωt − kr2 ) − (ωt − kr1 ) = kr1 − kr2 = k(r1 − r2 ) .

Согласно уравнению (6.23) результирующая амплитуда в заданной точке

A = A12 + A22 + 2A1 A2 cos(ϕ2 − ϕ1 ) .

Если ϕ2 − ϕ1 = ±2nπ , где n = 0, 1, 2,……., то А = А1 + А2, т. е. интерферирующие волны максимально усиливают друг друга.

Если ϕ2 − ϕ1 = ±(2n + 1)π , то A = A1 − A2 , т. е. интерферирующие волны максимально ослабляют друг друга. В частности, при А1 = А2 волны полностью гасят друг друга. При всех прочих значениях разности фаз волны лишь частично усиливают или ослабляют друг друга.

6.8.5. Стоячие волны

Волна, получающаяся при интерференции двух встречных плоских волн с одинаковыми частотами и амплитудами, называется стоячей.

Стоячая волна возникает при отражении плоской волны от какихлибо преград, например от поверхности раздела двух сред.

Уравнение плоской синусоидальной стоячей волны получается в результате сложения прямой ( ξ1 = Acos(ωt − kx) ) и обратной ( ξ2 = Acos(ωt + kx) ) волн, распространяющихся вдоль оси х.

ξ(x,t) = ξ1 (x,t) + ξ2 (x,t) = Acos(ωt − kx) + Acos(ωt + kx) = = 2Acos kx cos ωt.

Величина A(x) = 2Acos kx — амплитуда стоячей волны. Амплитуда зависит от координаты х.

Вточках, где kx = ±nπ (n = 0,1, 2,...) , амплитуда максимальна по абсолютной величине. Эти точки называются пучностями стоячей волны.

Вточках, где kx = ±(n + 12)π , амплитуда стоячей волны равна

нулю.

Эти точки называются узлами стоячей волны.

Расстояние между соседними пучностями так же, как и расстоя-

λ

ние между соседними узлами, равно 2 .

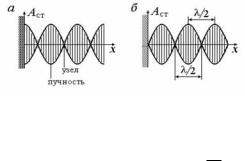
Фазы колебаний частиц, лежащих по разные стороны от узла, отличаются на π. Все частицы, находящиеся между узлами, колеблются в одинаковых фазах: все одновременно достигают крайних положений и одновременно проходят через нуль, но амплитуды колебаний этих частиц разные. На рис. 6.21 изображено мгновенное отклонения частиц от положения равновесия в стоячей волне.

Примером стоячей волны могут служить колебания струны. В местах закрепления струны всегда образуются узлы, поэтому в струне возможны

Рис. 6.21 только такие колебания, половина длины волны которых укладывается на длине струны A целое число раз

A = n λ2n ,

где n = 1, 2, 3, ... Длины волн λn соответствуют частотам колебаний струны

где u — фазовая скорость распространения колебаний вдоль струны. Частота, соответствующая n = 1, называется основной частотой струны. Частоты, соответствующие n = 2, 3, …, называются обертонами. В общем случае колебания струны складываются из колебаний основной частоты и обертонов.

Вопросы и задания для самопроверки

1.Как выразить через длину волны λ расстояние b между ближайшими точками на луче распространения волны, в которых фазы противоположны (например, между положительным и отрицательным максимумами)?

2.Как выразить параметры k и λ через циклическую ω и линейную ν частоты?

3.Какова длина бегущей волны, если разность фаз колебаний то-

π?Δϕ =

6

4.Какая из указанных величин (длина волны, скорость распространения волны, частота колебаний) изменяется при переходе волн из одной среды в другую?

5.Докажите, что стоячая волна ξ(x,t) = 2Acos kx cos ωt является результатом сложения двух противоположно направленных гармо-

нических волн одинаковой амплитуды и одинаковой циклической частоты.

6.Волны какого типа будут возбуждены в горизонтальном металлическом стержне, если ударить по концу молотком: а) сбоку; б) в торец?

7.Почему не могут быть поперечными упругие волны в газе?

8.Если известно, что из одной области среды в другую переносится энергия, то как определить, переносится ли она волнами или частицами вещества?

9.Обладает ли волновым фронтом плоская гармоническая вол-

на?

10.Может ли существовать в природе плоская гармоническая волна или это физическая идеализация, лишь приближенно описывающая реальность?

11.В чем различие бегущих и стоячих волн, плоских и сферических волн, продольных и поперечных волн?

Примеры решения задач

Задача 6.16

Длина волны λ = 5 м, частота колебаний ν = 3 Гц. Чему равна скорость u распространения волны?

Дано: λ = 5 м; ν = 3 Гц. Найти: u.

По условию задачи три полных колебания совершаются за время t = 1 с, т. е. за одну секунду через данную точку выбранной оси, вдоль которой распространяется волна, пройдут три гребня волны, отстоящие друг от друга на расстояние λ. Первый гребень (или любая другая фиксированная точка волны) переместится за одну секунду на расстояние 3 λ. Следовательно, скорость распространения вол-

ны u = 3λ . Подставив числовые значения, получим t = 3 15 =

u 45 м/с.

1

Ответ: скорость распространения волны u = 45 м/с.

Задача 6.17

На каком расстоянии A находятся две ближайшие точки в воде, совершающие колебания в противоположных фазах, если частота колебаний ν = 725 Гц, скорость звука в воде u = 1450 м/с.

Дано: u = 1450 м/с; ν = 725 Гц. Найти: A.

Две ближайшие точки, колеблющиеся в противофазе, находятся

Ответ: две ближайшие точки, колеблющиеся в противофазе, находятся на расстоянии 1 м.

Задача 6.18

Две точки, находящиеся на прямой на расстояниях х1 = 12 м и х2 = 15 м от источника волн, колеблются с разностью фаз Δφ = 0,75π. Найти длину волны λ, смещения указанных точек ξ(x1 ,t1 ) , ξ(x2 ,t1 ) в момент времени t1 = 1,2 и уравнение волны ξ(x,t) , если амплитуда колебаний A = 0,1 м, скорость распространения волны u = 20 м/с.

Дано: u = 20 м/с; Δφ = 0,75π; t = 1,2 с; А = 0,1 м; х1 = 12 м; х2 = 15 м. Найти: λ, ξ(x1 ,t1 ) , ξ(x2 ,t1 ) , ξ(x,t) = Asin ω(t − ux) .

Точки, находящиеся друг от друга на расстоянии, равном длине волны λ, колеблются с разностью фаз, равной 2π; точки, находящиеся друг от друга на любом расстоянии x, колеблются с разно-