
fizika
.pdf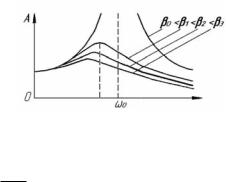
6.7. Вынужденные механические колебания |
371 |
Частота вынужденных колебаний совпадает с частотой возмущающей силы Ω и не зависит от свойств колеблющейся системы и среды (ω0 и β).
Вынужденные колебания даже при наличии сопротивления среды являются незатухающими. Амплитуда вынужденных колебаний может быть очень большой при малых значениях сопротивления среды и возмущающей силы, если частота возмущающей силы Ω близка к собственной частоте ω0.
И наоборот, амплитуда вынужденных колебаний может быть сколь угодно малой при больших значениях возмущающих сил, если частота возмущающих сил Ω сильно отличается от частоты ω0 (т. е. Ω << ω0 либо Ω >> ω0).
Амплитуда А вынужденных колебаний и величина θ, определяющая сдвиг фаз между вынужденными колебаниями и возмущающей силой, от начальных условий не зависят, но зависят от соотношения частот возмущающей силы и собственных колебаний.
Рассмотрим зависимость амплитуды вынужденных колебаний А от частоты возмущающей
силы Ω (рис. 6.14) при фиксиро- Рис. 6.14 ванных F0, ω0 и m.
Если Ω = 0 (сила F постоянна), то
F0 |
|
A = mω02 |
= , |
где — статическая деформация. Если Ω = ∞, то A → 0.
Если β = 0, то при Ω = ω0 А стремиться к бесконечности.
Это имеет место, когда коэффициент сопротивления среды равен нулю.
Если β ≠ 0, то при некоторой определенной для данного пружинного маятника частоте возмущающей силы Ωрез < ω0 амплитуда колебаний А достигает максимального значения.
Явление резкого возрастания амплитуды установившихся вынужденных колебаний при приближении частоты Ω внешней возмущающей

372 Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
силы к некоторой характерной для данного маятника частоте Ωрез получило название механического резонанса.
Чтобы найти резонансную частоту Ωрез для рассматриваемой системы, необходимо исследовать подкоренное выражение (6.46) на экстремум (при этом следует иметь в виду, что экстремумы амплитуды A (Ω) и подкоренного выражения f (Ω) противоположны).
Возьмем производную от подкоренной функции f (Ω) = (ω02 − Ω2 )2 + 4β2Ω2
по частоте Ω и приравняем ее к нулю
df (Ω) = 2(−2Ω)(ω2 − Ω2 ) + 8β2Ω = 0. dΩ 0
Из полученного равенства находится то значение аргумента Ω, при котором подкоренное выражение будет либо максимальным,
либо минимальным:
−4Ωω02 + 4Ω3 + 8Ωβ2 = 4Ω(−ω02 + Ω2 + 2β2 ) = 0 .
Так как Ω ≠ 0, то равенство имеет место только тогда, когда сомножитель (−ω02 + Ω2 + 2β2 ) = 0. Отсюда следует
Ω = ± ω02 − 2β2 .
Так как Ω — существенно положительная величина, то берем только положительное значение корня.
Чтобы выяснить, какой экстремум имеет место при значении ар-
гумента Ω = |
ω02 − 2β2 |
, необходимо взять вторую производную от |
||||||||||||||||||||||||||
функции f |
= f (Ω) и исследовать ее знак. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Если |
|
d 2 |
f |
> 0, то функция f |
= f (Ω) — минимальна, если |
d |
2 f |
< 0 , |
||||||||||||||||||||
|
dΩ2 |
d |
Ω2 |
|||||||||||||||||||||||||
|
|
|
f = f (Ω) — максимальна. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
то функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
d 2 f |
|
|
|
|
= −4ω |
2 |
+ 12Ω |
2 |
+ 8β |
2 |
= −4ω |
2 |
+ 12ω |
2 |
− 24β |
2 |
+ 8β |
2 |
= |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
dΩ2 |
Ω= ω02 |
−2β2 |
|
|
|
0 |
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 f |
= 8ω02 − 16β2 = 8(ω02 − 2β2 ) = 8Ω2 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Так как |
= 8Ω |
2 |
> 0 , то при частоте |
Ω = |
ω |
2 |
− 2β |
2 |
подкорен- |
|||||||||||||||||||
dΩ2 |
|
0 |
|
|||||||||||||||||||||||||
|
|
|
|
f = f (Ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ное выражение |
принимает минимальное значение, следо- |
|||||||||||||||||||||||||||
вательно, амплитуда колебаний А достигнет наибольшего (максимального) значения.

6.7. Вынужденные механические колебания |
373 |
Таким образом, амплитуда вынужденных колебаний А принимает максимальное значение, когда частота возмущающей силы равна
Ω = ω02 − 2β2 .
Частоту возмущающей силы, при которой амплитуда А достигает
максимального значения, называют резонансной частотой. |
|
Ωрез = ω02 − 2β2 . |
6.47 |
Из формулы видно, что резонансная частота Ωрез меньше частоты собственных незатухающих колебаний маятника ω0.
Зависимость A = A (Ω) называется резонансной кривой. На рис. 6.14 изображены резонансные кривые, соответствующие различным значениям коэффициента затухания (β0 = 0, β1 < β2 < β3). Максимум резонансной кривой тем выше и острее, чем меньше β. При отсутствии сопротивления среды (β0 = 0) амплитуда бесконечна (A → ∞).
При сооружении строительных объектов в сейсмических зонах необходимо учитывать резонансные явления. Собственная частота объекта должна отличаться от частоты колебаний земной коры, наблюдаемой в данной местности. В этом случае при землетрясении есть вероятность сохранения построенных зданий.
Вопросы и задания для самоподготовки
1.Почему незатухающие колебания в реальных системах могут быть только вынужденными?
2.Почему важен случай гармонического внешнего воздействия на колебательную систему?
3.Какие процессы наблюдаются при вынужденных колебаниях, когда частота возмущающей силы Ω приближается к собственной частоте ω0?
4.Что такое резонансная частота вынужденных колебаний, от чего она зависит?
5.Изменяется ли амплитуда вынужденных колебаний со временем при постоянной частоте возмущающей силы?
6.От каких параметров зависит амплитуда вынужденных колебаний?
7.Может ли амплитуда вынужденных колебаний быть бесконечно большой?
374 |
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
8. Почему при увеличении частоты возмущающей силы, действующей на колеблющуюся систему, амплитуда вынужденных колебаний достигает максимума, затем убывает?
Примеры решения задач
Задача 6.14
Тело совершает затухающие колебания с максимальным значением амплитуды А0 = 7 см, начальной фазой ϕ0 = 0, коэффициентом затухания β = 1,6 с–1. На это тело начала действовать внешняя периодическая сила, под действием которой установились вынужденные колебания. Уравнение вынужденных колебаний имеет вид
x2 (t) = 12sin(10πt − 0, 75π) см.
Найти уравнение (с числовыми коэффициентами) собственных
затухающих колебаний.
Дано: А0 = 7 см; ϕ0 = 0; β =1,6 с–1; x2 (t) = 12sin(10πt − 0, 75π) см. Найти: x (t).
Запишем уравнение затухающих колебаний в общем виде x(t) = A0e−βt sin(ωt + ϕ0 ) .
Чтобы записать приведенное уравнение с числовыми коэффициентами, необходимо вычислить циклическую частоту затухающих колебаний ω.
По тексту дано уравнение вынужденных колебаний x2 (t) = 12sin(10πt − 0, 75π) см,
где А = 0,12 м, Ω = 10π, ϕ = –0,75 π.
Обозначим начальную фазу вынужденных колебаний — θ и вы-
числим
tgθ = tg(−0, 75π) = −1 .
Начальная фаза вынужденных колебаний вычисляется по формуле (см. § 6.7)
tgθ = − |
2βΩ |
|
|
. |
|
ω02 − Ω2 |
||
Приравняв правые части представленных выражений, получим
−1 = − |
2βΩ |
. |
|
ω02 − Ω2 |
|||
|
|

6.7. Вынужденные механические колебания |
375 |
Собственная частота системы равна ω0 = |
Ω2 + 2βΩ . |
Частота затухающих колебаний равна ω = |
ω02 − β2 , |
ω = Ω2 + 2βΩ − β2 = (10π)2 + 2 1, 6 10π − 1, 62 = 10,5π.
Ответ: уравнение затухающих колебаний системы с числовыми коэффициентами имеет вид x(t) = 7e sin10,5πt (см).
Задача 6.15
Период затухающих колебаний системы T = 0,1 с, а отношение
амплитуд первого и одиннадцатого колебаний m = A1 = 21 . Опреде-
A11
лить резонансную частоту Ωp, коэффициент затухания β и на сколько резонансная частота меньше собственной частоты Δω данной колебательной системы.
Дано: T = 0,1 с; m = A1 = 21 . Найти: Ωp, β, Δω. A11
Резонансная частота вынужденных колебаний и период затухаю-
щих колебаний определяются по формулам |
|
|
|
|
|
|
|||||||||||||||
и |
|
|
|
|
Ω p = |
ω02 − 2β2 |
, |
|
|
|
|
|
|
(1) |
|||||||
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
T = |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
ω02 − β2 |
|
|
|
|
|
|
|
|
|
|||||
Собственная частота ω0 колеблющейся системы равна |
|
||||||||||||||||||||
T 2 = |
4π2 |
, |
ω2 − β2 |
= |
4π2 |
, |
|
ω |
|
= β2 |
+ |
4π2 |
. |
(2) |
|||||||
ω02 − β2 |
|
|
|
||||||||||||||||||
|
|
0 |
|
|
|
|
T 2 |
|
|
0 |
|
|
|
T 2 |
|
||||||
Из (1) и (2) находим резонансную частоту |
|
|
|
|
|||||||||||||||||
|
Ω |
|
= β2 + |
4π2 |
|
− 2β2 = |
|
4π2 |
− β2 . |
|
|
|
|||||||||
|
p |
T 2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
T 2 |
|
|
|
|
|
|
|||||
Для нахождения коэффициента затухания β запишем уравнение, связывающее первую и одиннадцатую амплитуды с учетом того, что время между первой и одиннадцатой амплитудой составляет 10 пе-
риодов и равно t = 10T.
A1 = A0e−βt ,
A11 = A0e−β(t +10T ) .

376 |
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
Из уравнений следует |
|
A |
= A e−β10T , |
11 |
1 |
A1 = 5β10T = m .
A11
Прологарифмировав последнее уравнение, получим ln m = β10T .
Вычислим первую неизвестную величину β
β= ln m = 3, 04 . 10T
Расчетные формулы и величины резонансной и собственной частоты системы равны соответственно
|
2π |
|
|
ln m |
|
|
2 |
|||||
Ω p = |
|
|
|
1− |
|
|
|
|
|
|
= 62, 76 рад/с, |
|
T |
|
|
|
|
||||||||
|
|
2π10T |
|
|||||||||
ω |
|
= |
β2 + |
4π2 |
|
= 62,83 рад/с. |
||||||
0 |
T 2 |
|||||||||||
|
|
|
|
|
|
|
|
|
||||
Ответ: резонансная частота Ωp = 62,76 рад/с, коэффициент затухания β = 3.04, резонансная частота Ωp меньше собственной ω0 на Δω = 0,07 рад/с. Собственная частота колебаний системы ω0 = 62,83 рад/с.
6.8.МЕХАНИЧЕСКИЕ ВОЛНЫ
6.8.1.Общие сведения о механических волнах
Если источник колебания (камертон, струна, мембрана и. т.д.) находится в упругой среде, то он приводит в колебательное движение соприкасающиеся с ним частицы среды. (Под частицей среды, совершающей вынужденные колебания, понимают малый элемент среды, размеры которого во много раз больше размеров молекул). Вследствие этого в прилегающих к источнику колебания частиц упругой среды возникают периодические деформации (например, сжатия и растяжения). При этих деформациях в среде появляются упругие силы, стремящиеся вернуть элементы среды к первоначальным состояниям равновесия. Из-за взаимодействия соседних элементов среды упругие деформации будут передаваться от одних участков среды к дру-
6.8. Механические волны |
377 |
гим с некоторой скоростью, зависящей от ее физических свойств. Частицы среды совершают колебательные движения около положений равновесия. От одних участков среды к другим передается только состояние деформации. Чем дальше расположена частица от источника колебаний, тем позднее она начнет колебаться. Распространение деформации от источника возмущения — процесс достаточно сложный, так как одновременно совершаются и колебания частиц около положения равновесия, и поступательное движение состояния колеблющихся частиц без перемещения самих частиц вдоль заданного направления. Состояние колеблющейся частицы среды и источника отличаются с увеличением расстояния между ними. Колебания во всех точках среды повторяют колебание источника с определенным запаздыванием, которое тем больше, чем больше расстояние от источника до точки среды. Если возмущения могут распространяться через упругую среду на большие расстояния, то каждая частица среды совершает колебания около своего положения равновесия в ограниченной области пространства. От точки к точке в упругой среде передается энергия механических колебаний, а не поток вещества.
При изучении распределенных колебаний в среде обычно не учитывают дискретное (молекулярное) строение среды и не рассматривают колебательное движение отдельных молекул. Среда рассматривается как сплошная и обладающая упругими свойствами.
Процесс распространения возмущений (деформаций) с конечной скоростью в упругой среде, несущий с собой энергию без переноса вещества, называется волной или волновым процессом.
В большинстве случаев источниками любых волн являются колебания.
Если источник совершает гармонические колебания, то и волна будет иметь форму синусоиды как в пространстве, так и во времени, причем каждая точка среды имеет свою амплитуду колебаний. Наиболее часто встречаются упругие волны.
Функция ξ = ξ(x,t) позволяет найти смещение от положения равновесия любой из частиц упругой среды в любой момент времени. Колебательное движение определяет смещение как функцию времени, а поступательное движение определяет зависимость функции ξ = ξ(x,t) от положения х. Таким образом, ξ = ξ(x,t) — функция двух переменных x и t.
378 |
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
Энергия, мощность (энергия, переносимая за единицу времени)
иинтенсивность (энергия, переносимая через единичную площадь поверхности за единицу времени) пропорциональны квадрату амплитуды волны.
Амплитуда волны уменьшается по мере удаления ее от источника обратно пропорционально расстоянию. Следовательно, энергия, мощность и интенсивность волн убывают по мере удаления от источника обратно пропорционально квадрату расстояния.
Волны в упругой среде бывают продольные и поперечные.
Волна называется продольной, если частицы среды колеблются в направлении распространения волны. Продольные упругие волны — это распространение деформации сжатия и растяжения. В жидких и газообразных средах распространяются только продольные волны. Объясняется это тем, что из-за текучести этих сред в поперечном направлении на частицы не действует возвращающая сила. Поэтому в них возбуждаются только продольные волны, распространяющиеся в виде чередующихся сжатий и разрежений среды.
Это свойство помогло геофизикам сделать вывод о существовании жидкого ядра Земли, поскольку обнаружено, что в диаметральном направлении сквозь Землю проходят только продольные волны, поперечные же никогда не регистрируются. Единственным возможным объяснением этого является наличие у Земли жидкого (расплавленного) ядра.
Волна называется поперечной, если частицы среды колеблются в направлении, перпендикулярном направлению распространения волны. Например, волна, бегущая по струне.
Втвердых телах упругие волны могут быть как продольными, так
ипоперечными.
Поперечные упругие волны — это распространение деформации сдвига, возможное только в твердых телах, где источник колебания деформирует кристаллическую решетку, сдвигая ее ячейки друг относительно друга.
В среде, в которой распространяется волна, можно выделить множество волновых поверхностей.
Волновой или фазовой поверхностью называются геометрическое место точек, в которых все частицы совершают колебания в одинаковой фазе.
6.8. Механические волны |
379 |
Волновые поверхности неподвижны. В зависимости от формы волновых поверхностей различают волны плоские, сферические, цилиндрические и т. д.
Область среды, охваченная волновым движением, называется волновым полем.
Граница, отделяющая возмущенную область среды от невозмущенной, или геометрическое место точек, до которых доходят колебания к данному моменту времени t, называется фронтом волны.
Фронт волны в отличие от волновых поверхностей все время перемещается.
Основными параметрами волны являются:
1.Гребни (пучности) — высшие точки волнового движения.
2.Впадины — низшие точки волнового движения.
3.Амплитуда волны А — максимальная высота пучности или глубина впадины, измеренная относительно положения равновесия.
4.Длина волны λ — расстояние между положениями ближайших частиц среды, колеблющихся со сдвигом фаз 2π (расстояние между двумя соседними пучностями или соседними впадинами).
5.Частота ν — число полных колебаний, совершаемых любой из частиц среды, в которой распространяется волна, за единицу времени (число гребней, проходящих через данную точку за единицу времени).
6.Период волны Т — промежуток времени, в течение которого любая частица среды совершает одно колебание (время, по истечении которого волна распространяется на расстояние, равное двум соседним пучностям или гребням).
7.Циклическая частота ω — число гребней, проходящих через данную точку за время, равное 2π секунды (число полных колебаний, со-
вершаемых за 2π секунд). G
8. Скорость распространения волны u — скорость, с которой перемещается пучность (впадина), вдоль заданного направления. Эту скорость называют фазовой скоростью, так как она характеризует перемещение в пространстве фазы колебаний.
(Не путать со скоростью колеблющихся частиц. Например, в случае поперечных волн скорость колеблющихся частиц перпендикулярна скорости распространения волны).

380 |
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
9. Волновой вектор kG |
– вектор, указывающий на направление |
распространения волны, по модулю равный k = |
2π |
, именуемый вол- |
|
λ |
|||
новым числом. |
|
||
|
|
Длина волны равна расстоянию, на которое волна распространяется за время, равное периоду, т. е. за период Т гребень проходит рас-
стояние, равное длине волны λ, |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
λ = uT . |
|
(6.48) |
||||||||||
Параметры волн связаны между собой соотношениями |
|
||||||||||||||
u = λ |
= λν = λ |
ω |
|
, |
(6.49) |
||||||||||
2π |
|||||||||||||||
|
|
T |
|
|
|
|
|
|
|
|
|
||||
так как |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
T = |
1 |
|
= |
2π |
. |
|
|
|
||||||
ν |
|
|
|
|
|||||||||||
|
|
|
|
|
|
ω |
|
|
|||||||
Учитывая (6.48), получим |
|
|
|
|
|
|
|
|
|
|
|
|
|||
k = |
2π |
= |
2π |
= |
|
2πν |
= |
ω . |
(6.50) |
||||||
|
uT |
|
|||||||||||||
|
λ |
|
|
u |
u |
|
|||||||||
Если колебания во всем пространстве имеют одинаковый период Т, следовательно, и одинаковую циклическую частоту ω = 2Tπ ,
то волна называется монохроматической. Если при распространении колебаний не происходит потери их энергии (например, переход механической энергии колебаний в тепловую), то колебания по мере удаления от источника не затухают и амплитуда колебаний повсюду оказывается одинаковой. Такая волна называется незатухающей. На практике упругие волны обладают конечным, хотя обычно малым затуханием. Упругие волны с частотой 16 ≤ ν ≤ 20000 Гц называются звуковыми или акустическими. Они воспринимаются человеческим ухом. В звуковой волне колебание в каждой точке среды совершает не только плотность среды, но и давление, а также температура. Распределение давления звуковой волны в пространстве называется звуковым полем.
