Геометрия Часть I.

1. ВЕКТОРЫ. Сложение векторов и умножение вектора на число. Коллинеарность и компланарность. Координаты вектора в аффинной системе координат. Скалярное и векторное произведения. Свойства, геометрический смысл этих произведений и их выражение в координатах.

   Сложение векторов и умножение вектора на число.

ОПР: Вектор – это направленный отрезок. Упорядоченная пара точек в пространстве.

О ПР: 1)Два вектора равны, если они имеют одинаковые длины и одинаково направлены.

2) Два вектора называются равными, если они совпадают с точностью до параллельного переноса.

ОПР: Суммой двух векторов a и b называется вектор, проведенный из начала a к концу b, если конец a и начало b совмещены.

AB + BC = AC (правило треугольника)

AB + AD = AC (правило параллелограмма)

ОПР: Произведением вектора на число называется такой вектор, длина которого равна произведению длины исходного вектора на число, а направление которого совпадает с исходным, если число больше 0 и противоположно ему, если число меньше нуля.

Свойства векторов.

1. a + b = b + a (коммутативность).

2. (a + b) + c = a + (b + c) (ассоциативность).

3. a + 0 = a (существование 0).

4. a + (-a) = 0 (существование противоположного).

5. (a + b) = a + b (дистрибутивность, относительно сложения векторов).

6. ( + )a = a + a (дистрибутивность, относительно сложения чисел).

7. (a) = ()a (ассоциативность).

8. 1a = a (существование единицы).

ОПР: Множество с заданными операциями сложения и умножения, на котором выполнены 8 свойств, называется векторным (линейным) пространством.

Коллинеарность и компланарность.

ОПР: Линейной комбинацией векторов a₁…a_n, с коэффициентами ₁…_n называется вектор a = ₁a₁ +…+ _n a_n.

ОПР: Система векторов 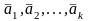называется линейно независимой, если тогда и только тогда, когда .

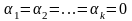ОПР: Система векторов называется линейно зависимой, если существует хотя бы один 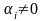такой, что ( ).

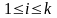Теорема: Векторы линейно зависимы , когда один из них можно представить в виде линейной комбинации остальных.

►()Векторы 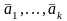линейно зависимы    хотя бы один :  .

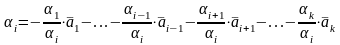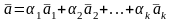
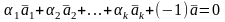()  , обозначим , .◄

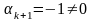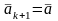ОПР: 1)Два линейно зависимых вектора называются коллинеарными.

2) Векторы называются коллинеарными, если они параллельны некоторой прямой.

ОПР: 1) Три линейно зависимых вектора называются компланарными.

2) Векторы называются компланарными, если они параллельны некоторой плоскости.

Координаты.

ОПР: Базисом на плоскости (в пространстве) называется упорядоченная пара (тройка) неколлинеарных (некомпланарных) векторов, лежащих в этой плоскости (пространстве). (Базисом в векторном пространстве называется упорядоченная линейно независимая система векторов такая, что любой вектор пространства – есть линейная комбинация векторов из этой линейно независимой системы)

Свойства координат вектора:

1⁰.

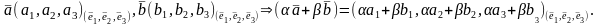
Сл1. Каждая координата суммы векторов равна сумме соответствующих координат слагаемых векторов.

Сл2. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

Сл3. При умножении вектора на число каждая его координата умножается на то же число.

2⁰.

Теорема: Любой вектор a пространства {плоскости} единственным образом представляется линейной комбинацией базиса (e₁, e₂, e₃) {(e₁, e₂)}: a = ₁e₁ + ₂e₂ + ₃e₃ {a = ₁e₁ + ₂e₂}.

► (!) Пусть существует другое разложение: a = ₁e₁ + ₂e₂: ₁  ₁, ₂  ₂, вычтем из одного разложения другое: (₁ - ₁)e₁ + (₂ - ₂)e₂ = 0. Векторы e₁, e₂ неколлинеарные, значит ₁-₁=0 и ₂ - ₂ = 0,  ₁ = ₁, ₂ = ₂. Противоречие. Значит разложение единственно.

( ) Отложим векторы e₁, e₂ и произвольный вектор a из одной точки O. Если a коллинеарен с одним из векторов базиса, то представление a через базис очевидно.

Если a неколлинеарен ни с одним из векторов базиса, то через конец a можно провести прямую l, которая параллельна прямой, содержащей один из векторов базиса. Пусть эта прямая параллельна e₁. На отложенной прямой l построим вектор e₁ с началом в точке пересечения прямой, содержащей e₂ и прямой l и концом общим с концом вектора a. На прямой, содержащей e₂ отложим вектор e₂ с началом в точке O и концом в точке пересечения e₂ и l. Тогда по правилу сложения векторов a = e₁ + e₂ = ₁e₁ + ₂e₂, где ₁ – коэффициент пропорциональности e₁ и e₁, ₂ – коэффициент пропорциональности e₂ и e₂. ◄

Аффинная система координат.

ОПР: Аффинной системой координат на плоскости называется точка (начало координат) и два неколлинеарных вектора (базис e¹ и e²), исходящие из начала координат.

Координаты в-ра в АСК – коэффициенты лин. комбинации при выражении в-ра через базис.

Радиус-вектор точки в АСК – в-р, с центром в начале СК и с концом в данной точке.

Координаты точки в АСК – координаты ее радиус-вектора.

Координаты в-ра – разность координат начала и конце в-ра.

Скалярное и векторное произведения.

ОПР: Скалярным произведением двух векторов a и b называется число, равное произведению длин этих векторов на косинус угла между ними: (a, b)=abcos.

ОПР: Тройка некомпланарных векторов a, b, c называется правой, если концы этих векторов, в порядке a,b,c расположены подряд по часовой стрелке, при условии, что они имеют общее начало.

ОПР: Векторным произведением двух векторов a и b называется вектор, длина которого равна произведению длин a и b на синус угла между ними, и направленный так, что тройка векторов a, b и [a, b] правая: [a, b]=absin.

Свойства скалярного произведения.

1. (a, b) = (b, a) (по определению).

2. (a, b) = 0  ab (по определению, cos/2 = 0).

3. (a, a) = a² (по определению, cos0 = 1).

4. (a, b) = (a, b) = (a, b).

5. (a, b + c) = (a, b) + (a, c).

6. Если в ортонормированном базисе векторы a и b имеют координаты (₁, ₂, ₃) и (₁, ₂, ₃), то (a, b) = ₁₁ + ₂₂ + ₃₃.

►6 свойство.

e₁,e₂,e₃ – прямоугольная (ортонормированная) система координат. (a, b) = (₁e₁+₂e₂+₃e₃, ₁e₁+₂e₂+₃e₃) = ₁₁(e₁,e₁)+₂₂(e₂,e₂)+₃₃(e₃,e₃)+… (остальные компоненты равны нулю по свойствам скалярного произведения) = ₁₁ + ₂₂ + ₃₃. ◄

Свойства векторного произведения.

1. [a, b] = - [b, a].

2. [a, b] = [a, b].

3. [a, b] = 0  a и b коллинеарные.

4. ([a, b],с) = <a, b, c> – объем ориентированного параллелепипеда, натянутого на a, b, c.

5. [a + b, c] = [a, b] + [a, c].

6. Если в ортонормированном базисе векторы a и b имеют координаты (₁, ₂, ₃) и (₁, ₂, ₃), то .

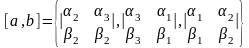ОПР: Объем ориентированного параллелепипеда, натянутого на в-ра a,b,c – наз-ся объем параллелепипеда, взятый со знаком +, если тройка в-ров a,b,c – правая, взятый со знаком –, если тройка в-ров a,b,c – левая.