
- •Геометрия Часть I.
- •Коллинеарность и компланарность.
- •Координаты.
- •Прямая и плоскость. Теорема о параметрическом уравнении прямой в пространстве. Теорема об общем уравнении плоскости в пространстве. Нормальный вектор и теорема о расстоянии точки от плоскости.
- •Нормальный вектор и теорема о расстоянии от точки до плоскости.
- •Кривые второго порядка. Канонические ур-ия эллипса, гиперболы и параболы. Каноническое уравнение эллипса.
- •Каноническое уравнение гиперболы.
- •Каноническое уравнение параболы.
- •Часть 2.
- •Деление отрезка.
- •Расстояние между двумя точками.
- •Объем параллелепипеда.
- •Вычисление скалярного, векторного и смешанного произведений по координатам множителей.
- •Основные типы уравнений прямой и плоскости. Угол между двумя прямыми. Расстояние от точки до прямой. Переход от общих уравнений к каноническим. Взаимное расположение прямой и плоскости.
Часть 2.
Преобразование координат. Деление отрезка. Расстояние между двумя точками. Объем параллелепипеда. Вычисление скалярного, векторного и смешанного произведений по координатам множителей.
Преобразование координат.
Oe1e2e3
– первая система координат, Oe1e2e3
–
вторая система координат. Запишем
координаты точки M=(x,
y,
z)
в новых координатах. Координаты начала
и базиса второй системы координат в
координатах первой системы имеют вид:
O=(x0,
y0,
z0),
e1=(a11,
a21,
a31),
e2=(a12,
a22,
a32),
e3=(a13,
a23,
a33).
Тогда
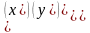 ,
где A
– матрица перехода (поворот), (x0,
y0,
z0)
– параллельный перенос начала координат.
,
где A
– матрица перехода (поворот), (x0,
y0,
z0)
– параллельный перенос начала координат.
На
плоскости в случае прямоугольных систем
координат матрица перехода есть
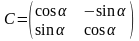 .
Где
– угол наклона новых осей к старым.
.
Где
– угол наклона новых осей к старым.
Деление отрезка.
Точка
М делит направленный отрезок АВ в
отношении R,
если
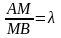 (если М лежит внутри АВ, то >0,
иначе <0).
(если М лежит внутри АВ, то >0,
иначе <0).
Расстояние между двумя точками.
Расстоянием
между двумя точками называется длина
вектора между этими точками и равно
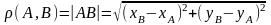 .
.
Объем параллелепипеда.
Ориентированным параллелепипедом наз-ся параллелепипед, натянутый на тройку некомпланарных векторов.
Объемом ориентированного параллелепипеда наз-ся объем параллелепипеда, натянутого на тройку некомпланарных векторов, если тройка векторов правая и объем параллелепипеда со знаком минус, если тройка векторов левая.
В
прямоугольной системе координат объем
ориентированного параллелепипеда равен
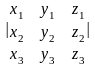 ,
где x,
y,
z
– векторы, на которые натянут
ориентированный параллелепипед.
,
где x,
y,
z
– векторы, на которые натянут
ориентированный параллелепипед.
Вычисление скалярного, векторного и смешанного произведений по координатам множителей.
Если в ортонормированном базисе векторы a и b имеют координаты (1, 2, 3) и (1, 2, 3), то (a, b) = 11 + 22 + 33.
Если в ортонормированном базисе векторы a и b имеют координаты (1, 2, 3) и (1, 2, 3), то .
([a, b],с) = <a, b, c> – объем ориентированного параллелепипеда, натянутого на a, b, c.
Основные типы уравнений прямой и плоскости. Угол между двумя прямыми. Расстояние от точки до прямой. Переход от общих уравнений к каноническим. Взаимное расположение прямой и плоскости.
Прямая:
Общее уравнение: Ax+By+C=0, где A, B, C – постоянные коэффициенты не равные нулю одновременно.
Уравнение прямой с угловым коэффициентом: у=kх+b.
Параметрическое уравнение прямой, проходящей через точку М0=(x0,y0) и вектор а=(1,2), коллинеарный М0М, где М – любая точка прямой:
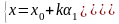 .
.Каноническое уравнение прямой, проходящей через точку М0=(x0,y0) вектор а=(1,2), коллинеарный М0М, где М – любая точка прямой:
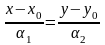 .
.Нормальное уравнение: xcos+ysin-p=0
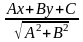 =0.
=0.Уравнение прямой, проходящей через 2 точки:
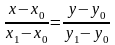 .
.Общее уравнение прямой в пространстве:
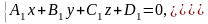
Плоскость:
Общее уравнение: Ax+By+Cz+D=0, где A, B, C, D – постоянные коэффициенты не равные нулю одновременно.
Параметрическое уравнение плоскости проходящей через точку М0=(x0,y0,z0) и пару неколлинеарных векторов а=(1,2,3) и b=(1,2,3), компланарных М0М, где М – любая точка плоскости:
 .
.Нормальное уравнение: xcos+ycos+zcos-p=0
 =0.
=0.Уравнение плоскости в отрезках:
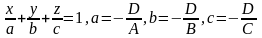 – отрезки, отсекаемые на Ох, Оу, Оz.
– отрезки, отсекаемые на Ох, Оу, Оz.Уравнение плоскости, проходящей через точку M=(x0,y0,z0) перпендикулярно вектору m=(A, B, C): A(x- x0)+B(y-у0)+C(z-z0)=0.
Уравнение плоскости, проходящей через 3 точки, не лежащие на одной прямой:
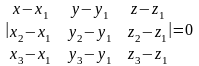 .
.
Угол между двумя прямыми.
Если
прямые заданы каноническими уравнениями,
то:
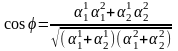 .
.
Расстояние от точки до прямой.
Расстоянием
от точки M0
до
прямой l
называется длина перпендикуляра,
опущенного из точки M0
на
прямую l.
(M0,
l)=x0cos+y0sin-p=
 =0.
=0.
Взаимное расположение прямой и плоскости.
l:
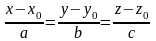 ,
:
Ax+By+Cz+D=0.
,
:
Ax+By+Cz+D=0.
l Аа+Bb+Cc0.
l Аа+Bb+Cc=0 и Ax0+By0+Cz0+D0.
l Аа+Bb+Cc=0 и Ax0+By0+Cz0+D=0.
Приведение уравнений квадрик к каноническому виду в плоскости. Канонические уравнения эллипсоида, гиперболоидов, параболоидов.
Любое уравнение линии второго порядка может быть приведено к одному из трех видов: 1)ax2+by2+c=0; 2)ax2+2by=0; 3)ax2+c=0.
Любое уравнение поверхности второго порядка может быть приведено к одному из пяти видов: 1) ax2+by2+cz2+d=0; 2) ax2+by2+2cz=0; 3) ax2+by2+d=0; 4) ax2+2by=0; 3)ax2+d=0.
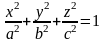 -
эллипсоид;
-
эллипсоид;
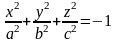 -
мнимый эллипсоид;
-
мнимый эллипсоид;
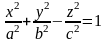 -
однополостный гиперболоид;
-
однополостный гиперболоид;
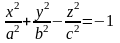 -
двуполостный гиперболоид;
-
двуполостный гиперболоид;
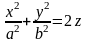 -
эллиптический параболоид;
-
эллиптический параболоид;
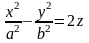 -
гиперболический параболоид;
-
гиперболический параболоид;
- эллиптический цилиндр;
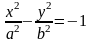 -
мнимый эллиптический цилиндр;
-
мнимый эллиптический цилиндр;
- гиперболический цилиндр;
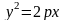 -
параболический цилиндр;
-
параболический цилиндр;
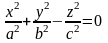 -
конус;
-
конус;
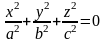 -
мнимый конус;
-
мнимый конус;
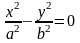 -
пара пересекающихся плоскостей;
-
пара пересекающихся плоскостей;
 -
пара мнимых пересекающихся плоскостей;
-
пара мнимых пересекающихся плоскостей;
x2 = a2 - пара параллельных плоскостей;
x2 = -a2 - пара мнимых параллельных плоскостей;
x2 = 0 - пара совпадающих плоскостей.
