2. Прямая и плоскость. Теорема о параметрическом уравнении прямой в пространстве. Теорема об общем уравнении плоскости в пространстве. Нормальный вектор и теорема о расстоянии точки от плоскости.

Теорема о параметрическом ур-ии прямой в пространстве.

В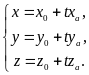 декартовой с-ме координат ур-ие прямой, проходящей через точку М₀(x₀,y₀,z₀) и имеющей направляющий вектор а={x_a,y_a,z_a}, будет:

►Пусть M(x,y,z) – произвольная точка пространства, она лежит на прямой, проходящей через точку М₀(x₀,y₀,z₀), коллинеарной в-ру а={x_a,y_a,z_a} тогда и только тогда, когда в-ры и а={x_a,y_a,z_a} коллинеарны, т.е. только тогда, когда или . Отсюда получаем параметрическое ур-ие.◄

Теорема об общем уравнении плоскости в пространстве.

Пусть в пространстве задана аффинная система координат. Уравнение Ax+By+Cz+D=0 (*)

является уравнением плоскости тогда и только тогда, когда A, B, C – постоянные коэффициенты не равные нулю одновременно.

► Необходимость. Пусть (*) – уравнение некоторой плоскость .Эту плоскость можно задать точкой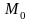 и направляющим подпространством 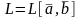. Тогда имеем:

Пусть Так как 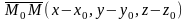, то

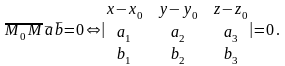
Разкладывая определитель по элементам первой строки, получим

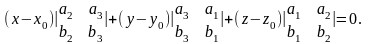
Следовательно, уравнение плоскости 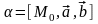имеет вид: Ax+By+Cz+D=0,

где

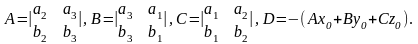
Достаточность. Пусть (*) – уравнение первой степени. Для определенности будем считать, что 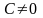. Зададим плоскость так, чтобы она проходила через точку и имела направляющими векторами вектор 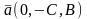и вектор 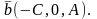Заметим, что координаты точки удовлетворяют уравнению (*), а координаты векторов и удовлетворяют уравнению Ax+By+Cz+D=0. По предыдущему пункту доказательства задается уравнением:

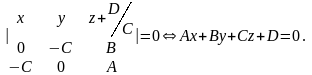
Так как уравнение (*) совпадает с уравнением плоскости , то (*) – уравнение плоскости .

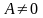Аналогично доказывается справедливость теоремы, если или .◄

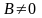Параметрическое уравнение плоскости:

Выражая компланарность векторов 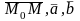через параметры, получим параметрическое уравнение плоскости.

В самом деле, из компланарности указанных векторов и неколлинеарности векторов и следует, что 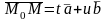, где t и u – однозначно определяемые числа (параметры т. М).

Представляя полученное векторное равенство в координатах, получим параметрическое уравнение плоскости

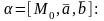
(1)

t, u – действительные числа.

Придавая различные значения для t и u, получим точки, принадлежащего плоскости .Верно и обратное: для любой точки плоскости найдется такая, причем единственная пара действительных чисел t и u, которые удовлетворяют (1).

Нормальный вектор и теорема о расстоянии от точки до плоскости.

Рассмотрим прямоугольную систему координат.

ОПР: нормалью к плоскости называется перпендикулярный вектор, проведенный к плоскости из начала координат.

Пусть в прямоугольной декартовой системе координат плоскость задана уравнением Если в этом уравнении имеет место равенство , т.е. 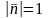, то уравнение называется нормальным уравнением плоскости.

Любое уравнение Ax+By+Cz+D=0 плоскости можно привести к нормальному виду. Для этого достаточно обе части этого уравнения разделить на

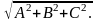
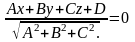- нормально уравнение прямой плоскости .

В самом деле

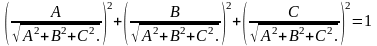
Т еорема: Пусть плоскость задана общим уравнением Ax+By+Cz+D=0, - произвольная точка. Тогда

►Очевидно, что , где .

Тогда - с одной стороны.

С другой стороны имеем:

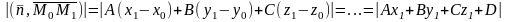. Отсюда следует, что: ◄