
fizika
.pdf6.2. Кинематика механических гармонических колебаний |
331 |
менты времени, когда осуществляются эти воздействия, задаются самой колеблющейся системой, т. е. система сама управляет внешним воздействием. Например, автоколебательной системой являются часы, в которых на маятник действует сила тяжести поднятой гири или сила упругости пружины. Эти действия происходят в моменты прохождения маятника через положение равновесия.
Различные по своей природе колебания (механические, электромагнитные и т. д.) обнаруживают много общего: они подчиняются одним и тем же закономерностям, описываются одними и теми же уравнениями, исследуются одними и теми же методами. Это дает возможность создать единую теорию колебаний. Рассмотрение теории колебаний в полном объеме требует знаний специальных разделов математики. Поэтому ограничимся рассмотрением лишь основ этой теории.
6.2. КИНЕМАТИКА МЕХАНИЧЕСКИХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
Простейшим типом периодических колебаний являются гармонические колебания. Закономерности, которым подчиняются гармонические колебания, важно знать потому, что многие реальные колебания близки к гармоническим, а периодические негармонические колебания есть результат сложения нескольких гармонических колебаний.
Рассмотрим механические гармонические колебания материальной точки.
Механическое гармоническое колебание — это такое прямолинейное неравномерное периодическое движение, при котором расстояние х от положения равновесия материальной точки до координаты, в которой в данный момент времени она находится, описывается уравнением
x = Asin(ω0t + ϕ0 ) , |
(6.1) |
где х — координата материальной точки в момент времени t.
Расстояние х материальной точки от положения равновесия до точки, в которой в данный момент времени она находится, называют смещением.
Наибольшее смещение материальной точки от положения равновесия называется амплитудой колебания и обозначается буквой A.

332 |
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
Аргумент при тригонометрической функции ϕ = ω0t + ϕ0 называется фазой колебаний. Фаза в процессе колебаний монотонно возрастает. За одно полное колебание она получает приращение, равное 2π. Величина ω0t — приращение фазы за промежуток времени t, величина ϕ0 — значение фазы в начальный момент времени. Коэффициент ω0 называют циклической (круговой или угловой) частотой.
Циклическая частота — величина, характеризующая быстроту изменения фазы с течением времени и равная приращению фазы за единицу времени,
ω0 |
= |
ϕ − ϕ0 |
. |
(6.2) |
|
||||
|
|
t |
|
|
Наименьший промежуток времени Т, по истечении которого значение изменяющейся физической величины повторяется:
—по модулю и направлению, если эта величина векторная,
—по величине, если она скалярная, называется периодом колебаний этой величины.
За период колебаний Т система совершает одно полное колебание. Число полных колебаний ν, совершаемых колеблющейся величиной за единицу времени, называется частотой колебаний. За единицу частоты принимается частота такого колебания, при котором за 1 с совершается одно полное колебание.
Частота измеряется в герцах (Гц). Период и частота колебаний свя-
заны соотношением ν = |
1 |
. |
|
|
|
|
|
|
|
||
T |
|
|
|
||
Установим связь между ω0 и Т. За время Т фаза возрастает на 2π. |
|||||
Подставив в (6.2) t = T и ϕ − ϕ0 |
= 2π , получим ω0 = |
2π |
= 2πν . Цик- |
||
|
|||||
|
|
|
|
T |
|
лическая частота определяет число полных колебаний за 2π с. |
|||||
|
|
|
Графическое представление |
||
|
|
|
уравнения гармонического коле- |
||
|
|
|
бания приведено на рис. 6.1 (Для |
||
|
|
|
наглядности построения графика |
||
|
|
|
значение начальной фазы ϕ0 = 0). |
||
|
|
|
Гармоническое колебание — |
||
|
|
|
движение пространственно огра- |
||
|
|
|
ниченное, т. е. в процессе колеба- |
||
Рис. 6.1 |
ний смещение материальной точки |
||||

6.2. Кинематика механических гармонических колебаний |
333 |
не выходит за пределы отрезка 2А. За одно полное колебание в каждой точке траектории колеблющаяся точка бывает дважды: один раз
— двигаясь в одном направлении, другой раз — в другом.
Найдем зависимости проекций скорости и ускорения от времени при гармонических колебаниях. С этой целью вычислим первую и вторую производные от (6.1)
vx |
= |
dx |
|
= Aω0 cos(ω0t + ϕ0 ) = Aω0 sin(ω0t + ϕ0 |
+ |
π ) , |
(6.3) |
|||||||||
dt |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
a |
|
= |
d 2 x |
= − Aω2 |
sin(ω |
t + ϕ |
|
) = Aω2 |
sin(ω |
t + ϕ |
|
+ π) . |
(6.4) |
|||
x |
dt2 |
|
|
|||||||||||||
|
|
0 |
0 |
|
0 |
0 |
0 |
|
0 |
|
|
|||||
Из (6.3 и 6.4) следует, что проекции скорости и ускорения гармонически колеблющейся материальной точки также совершают гар-
монические колебания с той же циклической частотой ω0 . Амплиту- |
||
ды соответственно равны Aω0 и Aω02 . Начальная фаза скорости равна |
||
|
+ |
π |
ϕ0 |
, т. е. разность фаз скорости и смещения постоянна и рав- |
|
|
|
2 |
на |
π |
(скорость опережает смещение на π ). Начальная фаза уско- |
|
2 |
2 |
рения равна (ϕ0 + π) , т. е. разность фаз колебаний ускорения и смещения постоянна и равна π (ускорение опережает смещение по фазе
на π). Графики зависимости смещения х, скорости vх и ускорения aх от времени при гармонических колебаниях для случая ϕ0 = 0 показаны на рис 6.2.
Из рис 6.2 видно, что смещение и ускорение при гармонических колебаниях происходят в противофазе, т. е. если смещение х максимально, то ускорение а минимально и находится в противофазе.
Величинафазы ϕ = ω0t + ϕ0
не влияет на форму кривой |
|
x(t), а определяет лишь ее по- |
|
ложение в произвольный мо- |
|
мент t. Частота и период ко- |
|
лебаний также не зависят от |
|
амплитуды. |
|
Траектория материаль- |
|
ной точки — движение про- |
|
странственно ограниченное, |
Рис. 6.2 |
334 |
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
периодическое, прямолинейное, не выходящее за пределы отрезка 2А.
Систему, совершающую гармонические колебания, называют (например, в электромагнетизме) гармоническим осциллятором.
Вопросы и задания для самопроверки
1.Приведите примеры колебаний, которые Вы наблюдали в окружающей действительности?
2.Можно ли считать гармоническим колебательным процессом суточное вращение Земли вокруг своей оси, годичное — вокруг Солнца?
3.Можно ли считать колебания дыхательной и сердечной деятельности гармоническими?
4.Покажите, что при гармонических колебаниях не только сама колеблющаяся величина, но и ее скорость и ускорение совершают гармонические колебания.
5.Покажите, что изменение координаты со временем опережает изменение скорости со временем по фазе на 1,57 радиан.
6.Что такое собственная частота гармонического осциллятора?
7.Если частица совершает гармонические колебания с амплитудой А, то, какое расстояние она проходит за один период?
8.Каким образом можно удвоить максимальную скорость гармонического осциллятора?
Примеры решения задач
Задача 6.1
Материальная точка совершает гармонические колебания с частотой ν = 10 Гц. В момент времени t = 0 точка имеет максимальное смещение хmax = 1 мм. Написать уравнение движения материальной точки.
Дано: ν = 10 Гц; хmax = 1 мм = 0,001 м.
Найти: уравнение движения материальной точки. Максимальное смещение точки от положения равновесия — ам-
плитуда колебаний хmax, циклическая частота колебаний ω0 = 2πν .
Уравнение имеет вид
x = xmax sin(2πνt + ϕ0 ) .
6.2. Кинематика механических гармонических колебаний |
335 |
Найдем начальную фазу ϕ0. Из условия задачи при t = 0 x = хmax, т. е.
xmax = xmax sin ϕ0 или 1 = sin ϕ0 , ϕ0 = (2k + 1) π2 , где k = 0, 1, 2,…
Изменение фазы на 2π не меняет колебаний, следовательно, достаточно рассмотреть случай k = 0. Получим начальный сдвиг фазы
ϕ0 = π2 .
Сучетом начального сдвига фазы уравнение движения материальной точки имеет вид
x= xmax sin(2πνt + π2 ) .
Если подставить численные значения, то x = 0, 01sin(2π10t + π2 ) , м.
Ответ: уравнение движения материальной точки имеет вид x = 0, 01sin(62,8t + π2 ) , м.
Задача 6.2
Материальная точка совершает гармонические колебания с частотой ν = 0,5 Гц. Амплитуда колебаний А = 3 см. Определить величины скорости и ускорения точки, когда смещение х = 1,5 см.
Дано: ν = 0,5 Гц; А = 3 см; х = 1,5 см. Найти: v, a.
Уравнение гармонических колебаний x = Asin(ω0t + ϕ0 ) .
Так как движение происходит вдоль оси х, то скорость всегда направлена вдоль этой оси.
Поскольку движение колебательное, то направление скорости может быть параллельной или антипараллельной оси х. Следовательно, проекция вектора скорости на эту ось vx = ± v , где v — модуль
скорости.
v = Aω0 cos(ω0t + ϕ0 ) .

336 |
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
Чтобы выразить скорость через смещение, нужно исключить из приведенных уравнений время. Для этого возведем оба уравнения в квадрат, разделим первое из них на А2, второе — на А2 ω02 и, сложив, получим
|
|
x2 |
+ |
v2 |
= 1 |
||||
|
|
A2 |
A2 |
ω02 |
|||||
|
|
|
|
|
|
||||
или, учитывая, что ω0 = 2πν , |
|
|
|
|
|
|
|||
|
x2 |
+ |
|
|
v2 |
|
= 1 . |
||
|
A2 |
|
4π2 ν2 A2 |
||||||
|
|
|
|
||||||
Решая полученное уравнение относительно v, находим |
|||||||||
|
v = 2πν |
A2 − x2 . |
|||||||
Ускорение |
|
|
|
|
|
|
|
||
ax |
= |
d νx |
− Aω02 |
sin(ω0t + ϕ0 ) = −ω02 x = −4π2 ν2 x . |
|
||||
|
|
dt |
|
|
Величина ускорения — положительная, поэтому a = 4π2 ν2 x . Ответ: величины скорости и ускорения равны
v = 8,2 см/с, а = 59,16 см/с2.
Задача 6.3
Точка совершает гармонические колебания. В некоторый момент времени t1 смещение х1 = 5 см. При увеличении фазы вдвое смещение точки стало х2 = 8 см. Найти амплитуду А колебаний.
Дано: х1 = 5 см; х2 = 8 см. Найти: А.
Уравнения гармонических колебаний для смещения в обоих слу-
чаях:
x1 = Asin(ω0t1 + ϕ0 ) ,
x2 = Asin(ω0t2 + ϕ0 ) . Согласно условию задачи
2(ω0t1 + ϕ0 ) = ω0t2 + ϕ0 .
Обозначим ω0t1 + ϕ0 = α ; тогда уравнения для смещения могут
быть представлены в виде
x1 = Asin α ,
x2 = Asin 2α = 2Asin α cos α .
6.3. Динамика механических гармонических колебаний |
|
|
337 |
||||||
Полученные уравнения преобразуем к следующему виду: |
|||||||||
x2 − |
x2 |
= |
A2 sin2 α − A2 sin2 α cos2 α = A2 sin4 α. |
||||||
2 |
|||||||||
|
|||||||||
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учитывая, что x1 |
= Asin α , получаем |
|
|
|
|||||
|
x2 |
|
x2 |
x4 |
4x4 |
|
|||
|
− |
2 |
= |
1 |
, откуда A = |
|
1 |
. |
|
|
1 |
|
4 |
|
A2 |
4x2 |
− x2 |
|
|
|
|
|
|
|
|
|
1 |
2 |
|
Ответ: амплитуда гармонических колебаний А = 8,3 см.
6.3. ДИНАМИКА МЕХАНИЧЕСКИХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
Выясним природу сил, создающих гармонические колебания. По второму закону Ньютона проекция силы, действующей на материаль-
ную точку, с учетом (6.4), равна |
|
F = ma = − Aω02 msin(ω0t + ϕ0 ) = −mω02 x . |
(6.5) |
Вывод: сила, вызывающая гармонические колебания, пропорциональна смещению колеблющейся точки от положения равновесия и всегда направлена положению равновесия.
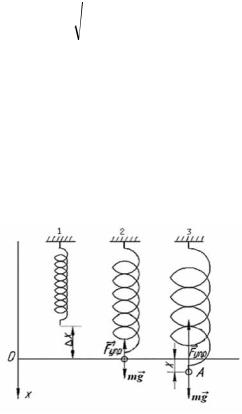
Рассмотрим колебания груза, висящего на пружине (рис. 6.3)
1. Если пружина растянута, то координата груза отрицательна, следовательно, проекция силы на ось х положительная. Это возможно, когда вектор силы параллелен оси х и
направлен к точке равно- весия. Рис. 6.3
2. Если пружина сжата, то координата груза положительна, следовательно, проекция упругой силы на ось х отрицательна. Это возможно, когда вектор силы антипараллелен оси х и направлен к точке равновесия. В положении равновесия сила, вызывающая колебания, на материальную точку не действует, т. е. при х = 0, F = 0.
338 |
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
Таким образом, условию (6.5) удовлетворяют упругие силы. Гармонические колебания могут быть вызваны также силами, которые не являются упругими по своей природе.
Вывод: силы, не являющиеся упругими по своей природе, но подобные упругим по характеру зависимости от координаты, называются квазиупругими.
Ниже приведены примеры колебаний систем, совершающихся в отсутствии сил трения и сопротивления среды.
6.3.1. Пружинный маятник
Пружинным маятником называют систему, состоящую из упругой невесомой пружины с коэффициентом упругости k и груза массой m.
На рис. 6.3 показаны: 1 — естественная длина пружины; 2 — состояние равновесия маятника; 3 — мгновенное состояние колеблющейся системы.
Составим дифференциальное уравнение колебаний пружинного маятника и найдем его решение. Начало координат совместим с положением равновесия маятника (положение 2 рис. 6.3). ОсьG х направим вертикальноG вниз. На груз действует сила тяжести mg и сила упругости Fупр′ . В положении равновесия векторная сумма сил, дейст-
вующих на груз, равна нулю
mgG + FGупр′ = 0 .
Проекция векторного уравнения на |
ось х |
|
|
− F ′ + mg = 0 или |
k |
x = mg , |
(6.6) |
упр |
|
|
|
где x — деформация пружины в состоянии равновесия, k — коэффициент упругости. Если груз отклонить от положения равновесия в ту или иную сторону, то результирующая сила, действующая на тело, не равна нулю. По второму закону Ньютона система придет в дви- жение с ускорением а mgG + FGупр
Если вектор ускорения aG в данный момент времени параллелен оси x, то проекция данного векторного уравнения на ось x имеет вид
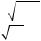
6.3. Динамика механических гармонических колебаний |
|
|
339 |
||||||
mg − k( x + x) = m |
d 2 x |
. |
|||||||
dt |
2 |
||||||||
|
|
|
|
|
|
|
|||
С учетом (6.6), обозначив ω02 |
= |
k |
, получим |
||||||
m |
|||||||||
|
d 2 x |
|
|
|
|
|
|
||
|
+ ω2 x |
= 0 . |
|
(6.7) |
|||||
|
|
|
|||||||
|
dt2 |
0 |
|
|
|
|
|
||
Второй закон Ньютона, записанный в форме (6.7), есть дифференциальное уравнение собственных колебаний груза на пружине в отсутствии силы сопротивления. Для решения этого уравнения воспользуемся методом Эйлера.
По этому методу решение уравнения (6.7) выберем в виде x(t) = Ceαt , где С — произвольная константа, α — неизвестная константа. Для
нахождения этих констант подставим |
|
|
|||
x(t) = Ceαt , |
dx(t) |
= Cαeαt , |
d 2 x(t) |
= Cα2eαt |
|
dt |
dt2 |
||||
|
|
|
|||
в (6.7), получим тождество
Cα2eαt + ω02Ceαt = 0 или Ceαt (α2 + ω02 ) ≡ 0 .
Так как из трех сомножителей два не равны нулю С ≠ 0 и eαt ≠ 0 , следовательно, (α2 + ω02 ) ≡ 0 . Отсюда вычисляется первая константа α:
α1,2 = ± −ω02 = ±iω0 , где i — мнимая единица, ( i = −1 ).
Двум значениям корня α1,2 соответствуют два частных решения. Общее решение находится как линейная комбинация двух частных решений
x = C*e+ iω0t + C*e−iω0t |
= т.к. e± iω0t |
= cos ω |
t ± i sin ω |
t |
= |
||||||||
1 |
|
2 |
|
|
|
|
0 |
|
|
0 |
|
|
|
= C* cos ω |
t + C*i sin ω |
t + C* cos ω |
t − C*i sin ω |
t = |
|
|
|||||||
1 |
0 |
1 |
0 |
|
2 |
0 |
|
2 |
0 |
|
|
|
|
|
= (C* + C* ) cos ω |
t + (iC* |
− iC |
* ) sin ω |
t. |
|
|
|
|
||||
|
1 |
2 |
0 |
|
1 |
|
2 |
0 |
|
|
|
|
|
Введем новые обозначения: C* + C* = C , iC* − iC* |
= C |
, получим |
|||||||||||
|
|
|
|
1 |
2 |
|
1 |
1 |
2 |
|
|
2 |
|
|
|
x = C1 cos ω0t + C2 sin ω0t . |
|
|
|
|
|
(6.8) |
|||||
Решение (6.8) запишем в форме |
|
|
|
|
|
|
|
|
|
||||
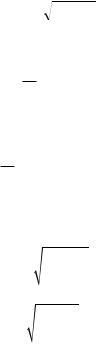
340 |
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
|
|
x = Asin(ω0t + ϕ0 ) |
(6.9) |
То, что выражения (6.8) и (6.9) эквивалентны друг другу, следует из тригонометрического тождества
Asin(ω0t + ϕ0 ) = A(cos ω0t sin ϕ0 + sin ω0t cos ϕ0 ) . |
(6.10) |
Из (6.8), (6.9) и (6.10) следует
C1 cos ω0t + C2 sin ω0t = Acos ω0t sin ϕ0 + Asin ω0t cos ϕ0 .
Приравняв соответствующие коэффициенты при одних и тех же
тригонометрических функциях, получим |
|
|
|||||
C1 = Asin ϕ0 , |
|
|
|||||
C2 = Acos ϕ0 , |
C1 |
|
|||||
A = C2 |
+ C2 , |
ϕ |
0 |
= arctg |
. |
||
|
|||||||
1 |
2 |
|
|
C2 |
|||
|
|
|
|
|
|||
Константы С1 и С2 находят из начальных условий, при этом лучше воспользоваться уравнением (6.8).
При t = 0, x = х0, dx начальная скорость.dt
Подставив начальные условия в уравнения x = C1 cos ω0t + C2 sin ω0t ,
dxdt = v = −C1ω0 sin ω0t + C2ω0 cos ω0t ,
получим
|
С1 = x0, C2 |
= |
v0 |
. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
ω0 |
|
|
|
|
|
|
||
Отсюда амплитуда и начальный сдвиг фазы равны |
|
|||||||||||||||||
A = |
x2 |
+ |
|
v2 |
, ϕ |
|
= arctg |
x |
ω |
0 |
|
|
|
|||||
|
|
0 |
0 |
0 |
|
|
. |
|
||||||||||
|
0 |
|
|
|
ω02 |
|
|
|
|
|
v0 |
|
|
|
|
|||
Уравнение колебания груза на пружине имеет вид |
|
|||||||||||||||||
x = |
x2 + |
|
v2 |
sin(ω |
t + arctg |
|
x |
ω |
0 |
) . |
|
|||||||
|
|
0 |
|
0 |
|
(6.11) |
||||||||||||
|
ω02 |
|
v0 |
|
||||||||||||||
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||
Зависимости скорости и ускорения груза от времени найдем, взяв производную от (6.9):
