fizika

Требование неизменности момента импульса системы тел подразумевает возможность изменения момента импульса каждого из тел системы.

Отношение кинетической энергии системы в конечный и начальный момент равно

где ω и ω′ — начальная и конечная угловая скорость системы (платформа и человек), Тн и Тк — начальная и конечная кинетическая энергии системы. Подставляя численные значения в (7–8), получаем

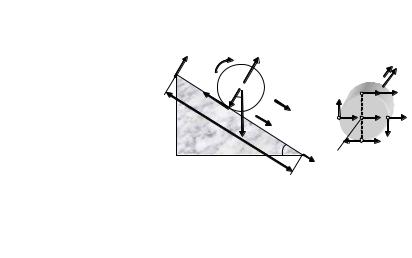
ки А, совершающей поступательное движение из начального положения в промежуточное. Отметим, что центр масс тела точка С при движении цилиндра совершает только поступательное перемещение. Из (рис. 5.7а) следует, что поступательноеG движение т. А совпадает с движением точки С. Вектор r′ — перемещение в системе отсчета К т. А из промежуточного положения в конечное. Последнее перемещение можно представить (рис. 5.7б) как вращение вокруг неподвижной оси в системе отсчета K ′ , жестко связанной с движу-

ния вокруг неподвижной оси, проходящей через центр масс. Таким

Так как при поступательном движении все точки тела движутся

Таким образом, плоское движение твердого тела можно представить как сумму поступательного движения его центра масс и вращательного движения относительно неподвижной оси, проходящей через центр масс.

Следовательно, кинетическая энергия плоского движения твердого тела равна сумме кинетической энергии поступательного движения его центра масс в инерциальной системе отсчета и кинетической энергии вращательного движения относительно оси, проходящей через его центр масс, т. е. в Ц-системе.

Вопросы и задания для самопроверки

1.Дайте определение плоского движения.

2.На какие два «простых» движения можно разбить плоское движение?

3.Запишите выражение для кинетической энергии плоского движения твердого тела.

силы Gреакции опоры NG и касательной составляющей — силе трения Fтр . При отсутствии скольжения сила трения есть сила трения покоя. Движение любой точки тела при плоском движении состоит из поступательного движения вместе с центром масс тела и вращательного вокруг центра масс. Следовательно, вектор скорости точкиG А равен сумме скорости поступательного движения центра масс vC и линейной скоростиG вращательного движения точки А относительно центра масс vл ( vл = ω r ). Для простоты мы не будем обозначать индексом Ц переменные, рассчитанные относительно центра масс системы. Так как результирующая скорость в точке А равна нулю, то скорость центра масс и линейная скорость вращения в этой точке цилиндра направлены в противоположные стороны и равны по модулю. Следовательно,

Способ 1

Запишем выражение (5.54) для вращательного движения цилин-

где IC и M – момент инерции и модуль момента внешних сил, ddtω > 0 , так как угловая скорость растет со временем. Моменты силG тяжести mgG и нормальной составляющей силы реакции опоры N равны нулю, линии действия этих сил пересекают ось вращения, проходящую через центр инерции цилиндра параллельно его образующей. Модуль момента силы трения равен

Запишем выражение (5.53) для поступательного движения центра

Учитывая (5), найдем связь между ускорением центра масс и си-

1+ IC 2 mR

Учтем, что момент инерции цилиндра относительно оси, проходя-

Способ 2

Применим закон сохранения энергии. На цилиндр действует неконсервативная сила трения. Так как скорость цилиндра в точке соприкосновения с наклонной плоскостью равна нулю, то равно нулю

318 Глава 5. ЭЛЕМЕНТЫ МЕХАНИКИ ТВЕРДОГО ТЕЛА

перемещение точки приложения силы. Следовательно, работа такой силы также равна нулю. Пусть тело в данный момент прошло вдоль наклонной плоскости путь X. Будем отсчитывать потенциальную энергию от этого положения тела. Тогда в верхней точке полная энергия тела состоит только из потенциальной энергии

В нижней точке наклонной плоскости у цилиндра нет потенциальной энергии, но есть кинетическая энергия поступательного и вращательного движения относительно центра масс

ОСНОВНЫЕ ПОЛОЖЕНИЯ

• УсловияG Gравновесия твердого тела

F = ∑ Fi = 0 ,

i

• УравненияG динамики твердого тела maGGC = F ,

dLdtЦ = MGЦ .

•Если силы лежат в плоскости XOY, то второе условие равновесия имеет вид

∑ Miz = ±∑ Mi = 0 ,

где Miz– проекция момента i-ой внешней силы на ось z, Mi = Fi l – модуль момента силы Fi, l — плечо силы.

• Момент инерции тела относительно оси

I = ∫ r2 dm ,

где r — расстояние от бесконечно малой части тела массой dm до оси.

•Момент инерции материальной точки

I = mr 2,

где r — расстояние от материальной точки с массой m до оси.

•Теорема Штейнера

I = IC + ma 2,

где I, IC — моменты инерции относительно произвольной оси и оси, проходящей через центр масс тела и параллельной первой, a – расстояние между осями,Gm – масса тела.

•Проекция момента импульсаG L твердого тела на ось z при его вращении со скоростью ω вокруг неподвижной оси (z направлена вдоль

оси)

Lz = Iωz.

•Основное уравнение вращательного движения твердого тела вокруг

неподвижной оси

Iεz = Mz,

где εz = dωz /dt – проекция углового ускорения на ось z.

•Закон сохранения момента импульса системы твердых тел при их вращательном движении вокруг неподвижной оси

Если Mz = 0, то Lz(t ) = Lz(t' ) или I(t )ωz(t ) = I(t' )ωz(t' ),

где t и t' – два момента времени, Mz — проекция суммарного момента внешнихG сил действующих на систему на ось z.

•Работа силы F над твердым телом при его вращательном движении

dA = Iω z dω z = M z dϕ ,

ϕ

A = ∫ M z dϕ ,

где ϕ0 – угол поворота тела, Mz – проекция момента силы на ось

•Кинетическая энергия вращения твердого тела вокруг неподвижной оси

T = Iω2 2 .

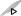
• Плоское движение твердого тела можно представить как поступа-