Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

fizika

.pdf

Скачиваний:

419

Добавлен:

17.05.2015

Размер:

4.42 Mб

Скачать

☆

<<< < Предыдущая 15 16 17 18 19 20 21 22 23 24 25 2627 / 4427 28 29 30 31 32 33 34 35 36 37 38 39 > Следующая >>>

4.7. Абсолютно твердое тело. Равнодействующая сил...			261
G равн	G Gравн	G G
M	=[r, F	] =[r, mg] ,	(4.41)
где mi – масса i частицы, m – масса системы частиц, rG			— радиус-век-

тор неизвестной точки приложения равнодействующей силы. С дру-

гой стороны,

G G

G равн

= ∑M

= ∑[r , F ] = ∑[r , m g] =[(∑m r ), g]

i i

i=1

Радиус-вектор центра масс системы по определению (4.28) равен

rGC =

∑mi rGi .

Умножим и поделим выражение для M равн на m. Тогда

G равн

G G

G G G

=[(∑mi ri ), g]

[(

∑mi ri ), mg] =[rC

, mg] .

(4.42)

i=1

m i=1

Приравнивая (4.39) и (4.40), получаем

[rG, mgG] =[rG , mgG

] .

Решением этого уравнения является вектор

rG = rG

+ const gG .

Если повернуть все силы тяжести относительно точек их приложения на один и тот же угол, то новая равнодействующая сила будет направлена в другую сторону. Можно показать, что все так полученные равнодействующиеG G силы тяжести имеют одну общую точку приложения r = rC , т. е. равнодействующая сил тяжести приложена к

центру масс системы. Точка, к которой приложена равнодействующая сил тяжести, называется центром тяжести системы. Следовательно, центр масс (инерции) и центр тяжести совпадают (совпадение — следствие приближения неизменности ускорения свободного падения в точках пространства, занятого системой частиц). Рассчи-

таем сумму моментов сил тяжести, приложенных к системе, относи-
тельно ее центра масс с учетом того, что rG							=0 (4.35).
					mi rGiЦ	СЦ		mi rGiЦ
G	G	G	G		mi rGiЦ	G		mi rGiЦ	G
MЦ	= ∑MiЦ	= ∑[riЦ , mi g] = ∑[				, mg	] =[∑		, mg] = (4.41)
MЦ	= ∑MiЦ	= ∑[riЦ , mi g] = ∑[			m	, mg	] =[∑	m	, mg] = (4.41)
	i=1	i=1	, mgG	i=1	m		i=1	m
		=[rG	, mgG	] =[0, mgG] = 0.
		СЦ

262	Глава 4. МОМЕНТ ИМПУЛЬСА. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

Таким образом, сумма моментов сил тяжести относительно центра масс твердого тела (т. е. в Ц-системе) равна нулю. Это равенство сохраняется при любом повороте твердого тела вокруг точки центра масс. Данное утверждение справедливо и для непрерывных твердых тел.

Вопросы и задания для самопроверки

1.Дайте определение Ц-системыG отсчета. G G

2.Чему равны: радиус-вектор rC , скорость vC и ускорение aC центра масс механической системы в Ц-системе отсчета?

3.Дайте определение равнодействующей сил, приложенных к абсолютно твердому телу.

4.К какой точке абсолютно твердого тела приложена равнодействующая сил тяжести?

	Примеры решения задач
Задача 4.6		L / 2					x
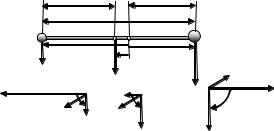
К концам гори-		L / 2	L				x
зонтального стержня			L
зонтального стержня			О C
длиной L = 1 м и мас-			О C
длиной L = 1 м и мас-		G					G
сой m = 2 кг подвеше-		G					G
сой m = 2 кг подвеше-	m1 gG	r1	G	Gr			r2	G
ны два груза массами	m1 gG	r1	G	Gr			r2	G
ны два груза массами	Gr		mg		Gr		m2 gG	M	2Ц Gr2
m1 = 1 кг и m2 = 3 кг.	Gr				Gr		m2 gG		2Ц Gr2
На каком расстоянии	1
На каком расстоянии	G		G
x от большей массы	M1Ц	G	M Ц			G
находится центр тя-		m1g				G		G
находится центр тя-					mg			G
жести системы?								m2 g
жести системы?

Дано: L = 1 м; m = 2 кг; m1 = 1 кг; m2 = 3 кг. Найти: x.

Выберем произвольно (например, на стержне) точку С и будем считать, что центр тяжести системы находится в этой точке. Тогда (4.41) сумма моментов сил тяжести всех частей системы относитель-

но точки С равна нулю, т. е.		G	G
G	G	G	G	= 0 .
∑ MiЦ	= M1Ц	+ MЦ	+ M2Ц	= 0 .	(1)

i=1

m2 − m1 + m 2

4.7. Абсолютно твердое тело. Равнодействующая сил...

263

Направление векторов определяем по поступательному движению правого винта, вращая его от радиус-вектора к вектору силы (4.3), а

модули — из (4.5). Следовательно,
G	G		G	G				G
М1Ц	↑↑ M Ц и		M1Ц	, M Ц M2Ц .					(2)
Модули векторов (4.5) равны соответственно
M1Ц	= m1 gr1 sin π / 2 = m1 g(					L		+ x)	,

				2
M Ц	= mgr sin π / 2 = mg(				L		− x) ,		(3)

				2
M2Ц = m2 gr2 sin π / 2 = m2 gx .
	G	G		G
Сумма трех векторов M1Ц		, M	Ц и M2Ц , лежащих на одной прямой,
равна нулю, только если
	M1Ц + M Ц = M2Ц .								(4)

Подставляя в (4) значения модулей векторов из (3), получаем урав-

нение
m g(	L	+ x) + mg(	L	− x) = m gx .	(5)
m g(		+ x) + mg(		− x) = m gx .	(5)
1	2	2		2
	2	2

Раскрывая скобки и перенося выражения, содержащие неизвест-

ное в левую часть уравнения, определяем x

m g

+ m gx + mg

− mgx = m gx

или

g ( m + m ) = (m − m + m) gx

m1 + m L

1+ 2 1 3 1

x =

= 0,375 м.

(6)

m − m + m

3 − 1+ 2

Ответ: x =

m1 + m

= 0,375 м.

264	Глава 4. МОМЕНТ ИМПУЛЬСА. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

4.8. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРА ТЯЖЕСТИ ТВЕРДОГО ТЕЛА

1. Симметрия

Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости, на оси или в

центре симметрии (рис. 4.15).

С		С	С
Отрезок прямой	Прямоугольник с вырезом		Эллипс с вырезом
С		С	С
С		С
Равносторонний треугольник		Цилиндр	Шар

Рис. 4.15

2. Разбиение

Если твердое тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести всего тела можно непосредственно вычислить по формулам (4.28). При этом число слагаемых в каждой из сумм будет равно числу частей, на которые разбито тело.

	E 4			F		K
	E 4		o		C3	K
	y	3 3	o		C3	p
	y	3 3				p
	y 2 2			M	C	L
B	y 2 2			C2	C
B		D
	С1 n		y1		N
A– 2					N
A– 2	– 1	O	1	2	4	6 х
	x1		x	2	x	3

Задача 4.7

Дана однородная плоская фигура ABDEFKLMN, состоящая из трех прямоугольников. Известны длины сторон всех прямоугольников, а значит, и координаты их центров симметрии.

4.8. Способы определения координат центра тяжести твердого тела

265

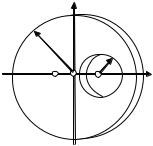
Найти координаты центра тяжести фигуры.

Дано: ABDO, OEFN, FKLM – прямоугольники; АВ = 1 м; BD = 2 м; ОE = 4 м; EF = 2 м; FK = 4 м; KL = 2 м.

Найти: xC, yC.

Определим координаты центров симметрии и площади прямоугольников, образующих фигуру ABDEFKLMN.

x1 = –1 м, y1 = 0,5 м, S1 = 2 м2, x2 = 1 м, y2 = 2 м, S2 = 8 м2, x3 = 4 м, y3 = 3 м, S3 = 8 м2,

S = S1 + S2 + S3 = 2 + 8 + 8 = 18 м2.

Получим формулы для определения координат центра тяжести произвольной фигуры, которую можно разбить на части, центры тяжести которых известны. Умножим числитель и знаменатель в пра-

вых частях выражения (4.28) на g
xC =	1	∑mi gxi ,	yC =	1	∑mi gyi ,	zC =	1	∑mi gzi .	(1)
	mg			mg			mg
		i			i			i

Так как фигура однородна, то введем плотность единицы площа-

ди фигуры σ [кг/м2]. Тогда
mi = σSi ,	(2)
m = σS ,	(3)

где m = ∑mi – вся масса и S = ∑ Si – вся площадь фигуры. Подстав-

ляя (2) и (3) в (1), получим

∑ Si xi

∑mi gxi

∑σSi gxi

σg

∑ Si xi

(4)

σSg

∑mi gyi

∑σSi gyi

σg

∑ Si yi

(5)

σSg

где ( xi , yi ) — координаты центра тяжести i части фигуры. Подставляя в (4.45) и (4.46) условия примера, получим координаты центра тяжести фигуры ABDEFKLMN:

x =	S1 x1 + S2 x2 + S3 x3	=	2(−1) + 8 1+ 8 4	=	38	= 2	1	м,

C	S	18		18		9

266		Глава 4. МОМЕНТ ИМПУЛЬСА. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
	y =	S1 y1 + S2 y2 + S3 y3	=	2 0,5 + 8 2 + 8 3	=	41	= 2	5	м,

	C	S	18		18		18

где S1, S2, S3 – площади первой, второй и третьей части фигуры, S = = S1 + S2 + S3.

Ответ: x =		S1 x1 + S2 x2 + S3 x3			= 2	1	м;

	C	S			9

y =	S1 y1 + S2 y2 + S3 y3		= 2	5	м.

C		S	18

3. Дополнение

Этот способ является частным случаем способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести твердых тел без выреза и вырезанной части известны.

Задача 4.8
y			Дан круг радиуса R = 3 м с вырезан-
			ным кругом радиуса r = 1 м. Расстояние
R			между центрами кругов a = 1 м. Найти
R			координаты центра тяжести фигуры.
C	r		координаты центра тяжести фигуры.
C	r	x	Дано: R = 3 м; r = 1 м; a = 1 м.
C1	C2	x	Найти: xC, yC.
C1	C2		Найти: xC, yC.
			Представим несимметричную фигу-
			ру как сумму двух симметричных фи-
			гур: сплошного круга радиуса R с плот-
			ностью единицы площади σ и сплош-

ного круга радиуса r с плотностью единицы площади — σ. Тогда в формулах (4) и (5) задачи 4.7 площадь круга радиуса r должна входить со знаком минус. В этом случае

S = πR2	, S		2	= −πr2	,
1			2		(1)
S = S + S					(1)
S = S + S		2	= π(R2 − r2 ).
1		2

Пусть С1 и С2 — центры (тяжести) сплошных кругов с радиусами R и r соответственно. Центр тяжести всей фигуры С лежит на прямой С1С2, так как эта линия является осью симметрии для круга с вырезом, т. е. yC = 0. Найдем xC. Поместим начало координат в центр сплошно-

Основные положения

267

го круга радиусом R и направим ось x вдоль прямой С1С2. Тогда абсциссы центров тяжести большого и малого кругов

x1 = 0, (2) x2 = a

x =

S x + S

= −

πar2

= −

ar2

1 1

2 2

π(R2 − r2 )

(R2 − r2 )

= −

1 12

= −

= −0,125

м.

− 1

Ответ: xC = −

ar2

= −0,125 м, yC = 0 м.

(R2 − r2 )

4.Интегрирование

Вобщем случае, если твердое тело нельзя разбить на несколько конечных частей, положение центров тяжести которых известно, то можно дискретную систему заменить на непрерывную и определить координаты центра тяжести системы по формулам (4.19), заменяя в них суммирование на интегрирование.

					LG	ОСНОВНЫЕ ПОЛОЖЕНИЯ
•	Момент				LG	импульса pG частицы
		G		G G
		L = [ r, p ],
	где rG			— радиус-вектор частицы.
•	Момент				G	G
•	Момент				M	силы F
		G		G	G
		M	= [ r, F ],
	где rG			— радиус-вектор точки приложения силы.
• Уравнение моментов (для частицы)
		dLG		G
			=	M ,
		dt	=	M ,
		dt	G
	где M – сумма моментов сил, действующих на частицу.

•Закон сохраненияG G момента импульса частицы:

если M = 0 , то L = const.

268		Глава 4. МОМЕНТ ИМПУЛЬСА. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
•	Момент L	импульса	pG частицы относительно оси z
	z
	Lz = L cosα,
	где α —угол между вектором LG			и осью z.
•	Момент M z	силы FG	частицы относительно оси z
	M z = M cosβ,		G
	где β — угол между вектором M и осью z.

• Уравнение моментов (для частицы) относительно оси

dLz = M z , dt

где M z – проекция суммы моментов сил на ось z.

• Закон сохранения проекции момента импульса частицы:

если M z = 0 , то Lz = const.

• Сумма внутренних сил и их моментов для системы частиц равна

нулю

FGвнут = 0 ,

M внут = 0 G.

•Момент L импульса системы частиц

LG = ∑ LGi ,

		Gi
где Li			— момент импульса i частицы.
• Уравнение моментов (для системы частиц)
	dLG		G	внеш
		= M			,

	dt G				G
где L			– момент импульса системы частиц, M внеш – сумма момен-

тов внешних сил, действующих на систему частиц.

•Закон сохраненияG моментаG импульса системы частицы:

если M внеш = 0, то L = const.

•Уравнение моментов (для системы частиц) относительно оси

dLdtz = M zвнеш ,

где Lz –проекция момента импульса системы частиц на ось z, M zвнеш – сумма проекций моментов внешних сил на ось z.

= MЦвнешz .

dLЦz

Обозначения, используемые в главе 4									269
• Закон сохранения проекции момента импульса системы частиц:
если		M внеш = 0 , то L					= const.
			z			z
• Радиус-вектор центра масс
rGC =	1		∑mi rGi ,		m = ∑mi
rGC =	m		∑mi rGi ,		m = ∑mi
	m		i	G			i
где m и				r – масса и радиус-вектор i частицы.
		i		i
• Скорость и ускорение центра масс
G		drGC		G	dvGC			d 2 rGC
v =				и a =		=
v =		dt		и a =	dt	=		dt2
C		dt		C	dt			dt2

• Ц-система — система отсчета, жестко связанная с центром масс и

перемещающаяся без вращения относительно инерциальной системы отсчета.

• УравнениеG моментов для Ц-системы

dLdtЦ = MGЦвнеш ,

•Центр тяжести — точка приложения равнодействующей сил тяжести. Совпадает с центром масс.

•Сумма моментов сил тяжести относительно центра масс равна нулю.

ОБОЗНАЧЕНИЯ, ИСПОЛЬЗУЕМЫЕ В ГЛАВЕ 4

pG — вектор импульса частицы

LG — вектор момента импульса частицы

FG — вектор силы

M — вектор момента силы

lG — плечо импульса или силы vG — вектор скорости

a — вектор ускорения m — масса частицы

tG — время

g — вектор ускорения силы тяжести

270			Глава 4. МОМЕНТ ИМПУЛЬСА. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
				ТЕСТЫ ДЛЯ ЭЛЕКТРОННОГО ЭКЗАМЕНА
			Момент импульса частицы. Момент силы
G	T4.1 Если pG — импульс, а rG — радиус-вектор частицы, то момент
L	импульса частицы равен					G	G	G G	G G
	GG			G G		G	G	G G	G G
1) rp			2) [ p, r ]		3) [ r, p ]			4) m [ r, p ]	5) –[ r, p ]
	T4.2 Если pG			— импульс, а l		— плечо импульса, то модуль момен-
та LG импульса частицы равен
1) l p2			2) p		3) l 2p			4) l p	5) l 2p2
	T4.3 Если модуль импульса равен 10 м/c, а плечо импульса равно
5 м, то модуль момента импульса равен
1) 500 м3/c2			2) 10 м/c		3) 250 м3/c			4) 50 м2/c	5) 2500 м4/c2
	T4.4 Если FG			— сила, а rG		— радиус-вектор точки приложения
				G
силы, то момент M силы равен								G G	G G
1)	G		2)	GG	GG			G G	G G
1)	F		2)	Fr	3) rF			4) [ F, r ]	5) [ r, F ]	G
			G							G
	T4.5 Если F — сила, а				l — плечо силы, то модуль момента M
силы равен			2) l 2 F						5) F
1) lF			2) l 2 F		3) l F 2			4) l 2F2	5) F
	T4.6 Если модуль силы равен 10 Н, а плечо силы равно 2 м, то мо-
дуль момента силы равен
1) 20 Н·м			2) 40 Н · м2		3) 200 Н2 · м			4) 400 Н2 · м2	5) 10 Н
			G
G	T4.7 Если M – момент силы, а β – угол между осью z и вектором
M , то проекция момента силы на ось z равна
1) M z		= M sin β		2) M z	= L cosβ
3) M z		= Mtgβ		4) M z = Mctgβ			5) M z = M cosβ
	T4.8 Если F = 10 Н, l = 2 м, β = 60°, где F — сила, l — плечо силы,
								G	G
β — угол между осью z и вектором момента M силы									F , то проекция
момента силы на ось z равна
1) 30 Н			2) 10 Н · м		3) 20 Н2 · м			4) 40 Н · м2	5) 100 Н · м
				Уравнение моментов
			G					G
	T4.9 Если L – момент импульса частицы, а M – векторная сум-

ма моментов сил, приложенных к частице, то уравнение моментов имеет вид

<<< < Предыдущая 15 16 17 18 19 20 21 22 23 24 25 2627 / 4427 28 29 30 31 32 33 34 35 36 37 38 39 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.03.2016138.75 Кб199ESSE_Ilyasov_V_A_PSv_-313.doc
#
17.05.2015586.32 Кб161Example12.pdf
#
17.05.2015402.77 Кб280Fil_Test_dlya_2014_may.docx
#
17.05.20152.8 Mб173final_zapiska_arkh.doc
#
17.05.201532.76 Mб631Finansy_i_kredit_lektsii_moi.doc
#
17.05.20154.42 Mб419fizika.pdf
#
22.11.2019157.7 Кб173flp.doc
#
17.05.201537.37 Кб212Formuly_matem.docx
#
13.08.2019265.51 Кб210Geometria.docx
#
17.05.20152.48 Mб321GOS_NovyE.pdf
#
15.04.2019140.29 Кб38history_usu.doc