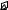fizika
.pdf
5.4. Вращение твердого тела вокруг неподвижной оси... |
291 |
Уравнение (5.27) называется основным уравнением вращательного движения или вторым законом Ньютона для вращательного движения. В отличие от поступательного при вращательном движении твердого тела вокруг неподвижной оси одинаковыми являются только угловые характеристики движения всех точек. Следовательно, кинематика вращательного движения тела совпадает с кинематикой вращательного движения точки. Поэтому
|
ω z = ω0 z + ∫t |
ε z dt , |
|
|
|
(5.28) |
||
|
ϕ z = ϕ0 z + ∫t |
0 |
+ ω0 z t + ∫t |
∫t |
|
|
||
Если εG |
ω z dt = ϕ0 z |
ε z dt . |
(5.29) |
|||||
0 |
|
|
|
0 |
0 |
|
|
|
= const ( ε z = const ), то |
|
|
|
|
|
|
||
|
ωz = ω0z + εzt , |
|
|
|
(5.30) |
|||
|
ϕ z = ϕ0 z + ω0 z t + |
ε z t2 |
. |
|
|
(5.31) |
||
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
Непрерывная система частиц
Во многих случаях удобнее рассматривать твердое тело как непрерывную среду. Для этого твердое тело мысленно разбивают на бесконечно малые частицы с бесконечно малой массой dm. Заменяя в уравнении (5.24) Ii → dI и mi → dm , получаем определение бесконечно малого момента инерции бесконечно малой массы dm в виде (рис. 5.5)
dI = R2 dm , |
(5.32) |
где R — расстояние от бесконечно малой частицы до оси вращения. Тогда для нахождения момента инерции непрерывной системы частиц
относительно некоторой оси |
z |
ΩG |
|
вместо суммирования конеч- |
|
||
ного числа конечных момен- |
|
|
|
тов инерции отдельных частиц |
|
|
|
в выражении (5.24) надо сум- |
|
|
|
мировать (интегрировать) бес- |
|
R dm |
dpG dmvG |
конечно большое число беско- |
|
|
|
нечно малых моментов инер- |
|
|
|
ции отдельных частиц, т.е. |
|
Рис. 5.5 |
|
292 |
Глава 5. ЭЛЕМЕНТЫ МЕХАНИКИ ТВЕРДОГО ТЕЛА |
|
|
I = ∫ R2 dm . |
(5.33) |
|
V |
|
Непрерывное распределение массы в пространствеG в общем случае характеризуется объемной плотностью ρ(r ) , которая определяется как отношение бесконечно малой массы тела dm к бесконечно ма-
лому объему этой массы dV, т. е. |
|
|
|
G |
dm |
|
|
ρ(r ) = |
|
, |
(5.34) |
dV |
|||
где rG — радиус-вектор, определяющий положение бесконечно малой |
|||
массы в пространстве в некоторой системе координат. Тогда |
|
||
dm = ρ(rG)dV . |
(5.35) |
||
Так же, как и плотность тела ρ(rG) , расстояние от любой точки телаG до оси вращения зависит от радиус-вектора этой точки, т. е. R = R(r ) .
Из (5.35) и (5.33) получаем выражение для определения массы тела и его момента инерции относительно некоторой неподвижной оси
|
m = ∫ dm = ∫ρ(rG)dV , |
(5.36) |
||||
|
|
|
V |
|
||
I = ∫ dI = ∫ R2 dm = ∫ρ(rG)R(rG)2 dV = ∫ ∫ ∫ ρ(x, y, z)R(x, y, z)2 dxdydz .(5.37) |
||||||
|
V |
V |
|
|||
В простейшем случае, когда тело однородно, т. е. ρ(rG) = const , и |
||||||
|
ρ = |
m |
= const . |
(5.38) |
||
|
|
|||||
Тогда |
V |
|
|
|
|
|
dm = ρdV , |
|
|||||
|
(5.39) |
|||||
I = ∫ ∫ ∫ ρ(x, y, z)R(x, y, z)2 dxdydz = |
m |
∫ ∫ ∫ |
R(x, y, z)2 dxdydz . (5.40) |
|||
|
||||||
|
V |
|
V V |
|
||
Если интегрирование происходит по объему тела, то интеграл называется объемным. Он достаточно легко вычисляется, когда подынтегральное выражение и тело, по объему которого производится интегрирование, обладают какимлибо типом симметрии: плоской, осевой, цилиндрической или сферической. В этих случаях объемный интеграл легко сводится к определенному интегралу. Отметим, что момент инерции — величина аддитивная (как и масса). Это означает, что момент инерции тела относительно любой оси всегда равен сумме моментов инерции относительно этой же оси его частей. Момент инерции величина неотрицательная.
294 |
|
Глава 5. ЭЛЕМЕНТЫ МЕХАНИКИ ТВЕРДОГО ТЕЛА |
||
∑ |
m RG′2 |
= I ′ = I |
C |
, |
i i |
|
|
||
i
где IC – момент инерции относительно произвольной точки оси z′ , проходящей через центр масс тела. Из (4.29, 4.35) следует, что
|
|
|
∑mi rGi′ |
|
|
|
||
|
|
∑mi rGi′ = m |
i |
|
= mrGСЦ = 0 , |
|||
|
|
m |
|
|||||
|
|
i |
∑mi rGi |
|
|
|
||
|
∑ |
|
|
′ |
G |
|||
|
|
|
|
i |
|
|
||
так как |
m = m — масса тела, а |
|
|
|
= rСЦ = 0 — радиус-вектор |
|||
|
|
|
|
|||||
|
i |
|
|
m |
|
|
|
|
|
i |
|
|
|
|
|
|
|
центра масс системы, рассчитанный в системе отсчета, связанной с центром масс, т. е. в Ц-системе. Разложим радиус-вектор центра масс системы и все радиус-векторы точек системы на сумму двух взаимно перпендикулярных векторов: параллельных оси z и лежащих в плоскости, перпендикулярной оси z.
G |
|
G |
|
|
G |
|
|
1 |
|
G |
|
1 |
|
G |
|
G |
|
1 |
|
G |
1 |
|
G |
|
r |
′ = r |
′ |
|
+ r |
′ |
= |
|
|
m r |
′ = |
|
|
m (r |
′ |
+r |
′ ) = |
|
|
m R′ + |
|
|
m r |
′ = 0 . |
|
|
m |
∑i |
m |
∑i |
m ∑i |
m ∑i |
||||||||||||||||||
Ц |
Ц |
|
Ц& |
|
i i |
|
i i |
|
i |
& |
i i |
i i |
& |
|||||||||||
Если сумма двух взаимно перпендикулярных векторов равна нулю, то и каждый из этих векторов равенG нулю. Следовательно,
∑mi Ri′ = 0 .
|
|
|
|
i |
|
|
|
|
Тогда |
G |
|
G |
G |
G2 |
|
|
|
|
2 |
= IC + ma |
2 |
. |
||||
|
I = ∑mi Ri′ |
|
+2a |
∑mi Ri′ +∑mi a |
|
|||
|
i |
|
|
i |
i |
|
|
|
Вопросы и задания для самопроверки
1.Линейные или угловые скорости являются одинаковыми для всех частиц системы при ее вращении относительно неподвижной оси?
2.Как связаны между собой вектор линейной скорости частицы
ивектор ее угловой скорости?
3.Как связаны между собой вектор момента импульса частицы и вектор ее угловой скорости при вращательном движении вокруг неподвижной оси?
4.Дайте определение момента инерции частицы и системы частиц.
5.4. Вращение твердого тела вокруг неподвижной оси... |
295 |
5.В каких единицах измеряется момент инерции?
6.Запишите второй закон Ньютона и основное уравнение вращательного движения.
7.Сформулируйте теорему Штейнера.
Примеры решения задач
Задача 5.4
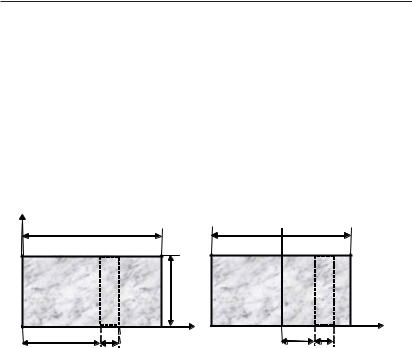
Определить момент инерции прямоугольной пластины длиной L, шириной b и массой m относительно оси, параллельной ее боковой стороне и: 1) проходящей через боковую сторону, 2) проходящей через середину пластины (центр масс).
y |
L |
|
|
y |
L |
|
|
|
|
|
|
||
|
|
|
b |
|
|
|
O |
dх |
|
х –L/2 |
O х |
dх |
L/2 х |
х |
L |
|||||
|
а |
|
|
|
б |
|
Дано: m — масса пластины; L — длина пластины; b — ширина пластины.
Найти: I — момент инерции пластины (стержня).
Площадь сплошной однородной прямоугольной пластинки и ее
поверхностная плотность равны |
|
||
S = Lb , |
(1) |
||
σ = |
m |
. |
(2) |
|
|||
|
S |
|
|
Направим ось х вдоль стороны пластинки, длина которой L. Рассмотрим часть пластинки в виде бесконечно тонкой полоски, параллельной оси Оу и расположенной на расстоянии х от нее (рис. а). Ширина полоски бесконечно мала и равна dx. Тогда площадь ds и масса dm этой бесконечно тонкой полоски
ds = bdx , |
(3) |
296 |
|
Глава 5. ЭЛЕМЕНТЫ МЕХАНИКИ ТВЕРДОГО ТЕЛА |
|||||
dm = σ ds = |
m |
ds = |
m |
bdx = |
m |
dx . |
(4) |
S |
Lb |
|
|||||
|
|
|
L |
|
|||
Все точки бесконечно тонкой полоски пластины находятся на одинаковом расстоянии от оси у. Следовательно, момент инерции бес-
конечно тонкой полоски (5.32) |
|
||
dI = r2 dm = x2 |
m |
dx . |
(5) |
|
|||
|
L |
|
|
Момент инерции всей пластинки относительно оси равен сумме моментов инерции относительно той же оси всех бесконечно тонких полосок, на которые можно разрезать пластинку. Тогда получаем (5.37)
I = ∫ dI = ∫ x2 dm = ∫L |
m |
x2 dx = |
m |
|
x3 |
|
L |
= |
mL2 |
. |
(6) |
|
|
||||||||||
L |
L 3 |
|
|
|
|||||||
0 |
|
|
0 |
3 |
|
|
|||||
|
|
|
|
||||||||
Если рассчитать момент инерции пластинки относительно оси, проходящей через середину пластинки (рис. б) вдоль оси у, то
I = I |
C |
= ∫ dI = ∫ x2 dm = L∫/ 2 |
m |
x2 dx = |
m |
|
x3 |
|
|
L/ 2 |
= |
mL2 |
. |
(7) |
|
|
|
|
|||||||||||||
|
|
|
|
||||||||||||
|
− L/ 2 L |
|
L 3 |
|
-L/ 2 |
12 |
|
|
|||||||
|
|
|
|
|
|||||||||||
Очевидно, что момент инерции не зависит от ширины пластинки b. Следовательно, результат справедлив и для пластинки с бесконечно малой шириной, т.е. для стержня длиной L и массой m. Еще раз подчеркнем: момент инерции любого тела можно определить только тогда, когда известно, относительно какой оси он должен рассчитываться.
Ответ: 1) I = |
mL2 |
, 2) |
IC = |
mL2 |
(для прямоугольной пластины и |
|||||
3 |
|
|||||||||
стержня). |
|
12 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Задача 5.5 |
|
|
|
|
|
|
|
|
|
|
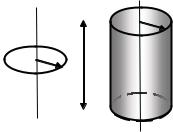
Определить момент инерции цилин- |
|
|
|
R |
|
|||||
|
|
|
|
|||||||
дрической поверхности высотой H, ра- |
|
|
|
|
||||||
|
|
|
|
|||||||
диусом основания R и массой m отно- |
|
|
|
|
|
|||||
сительно оси, проходящей через центр |
R |
H |
|
|
||||||
основания поверхности параллельно ее |
|
|
|
|
|
|||||
направляющим. |
|
|
|
|
|
|
|
|
|
|
Дано: m — масса цилиндра; H — вы- |
|
|
|
|
|
|||||
|
|
|
|
|
||||||
сота цилиндра;R — радиус основания. |
|
|
|
|
|
|||||
|
|
|
|
|
||||||
5.4. Вращение твердого тела вокруг неподвижной оси... |
|
|
297 |
||
Найти: I — момент инерции цилиндрической поверхности. |
|
||||
Так как ось проходит через центр симметрии цилиндрической по- |
|||||
верхности (а значит и церез точку центра масс), то I = IC. Так как все |
|||||
точки цилиндрической поверхности находятся на одинаковом рас- |
|||||
стоянии R от оси цилиндра, то выражение (5.33) сводится к виду |
|||||
I = IC = ∫ r2 dm = R2 ∫ dm = mR2 . |
|
(1) |
|||
Результат не зависит от высоты цилиндрической поверхности H. |
|||||
Следовательно, он справедлив для цилиндрической поверхности бес- |
|||||
конечно малой высоты, т. е. для обруча радиуса R и масссой m. |
|
||||
Ответ: IC = mR2 (для цилиндрической поверхности и обруча). |
|||||
Задача 5.6 |
|
|
|
|
|
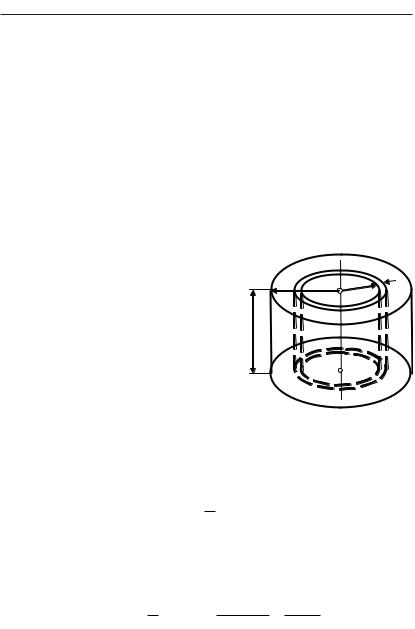
Определить момент |
инерции |
|
|
|
|
сплошного цилиндра высотой H, ра- |
|
R |
r |
dr |
|
диусом основания R и массой m от- |
|
|
|||
|
|
|
|
||
носительно оси, проходящей через |
|
|
|
|
|
центр цилиндра параллельно его на- |
H |
|
|
|
|
правляющим. |
|
|
|
|
|
|
|
|
|
|
|
Дано: m — масса цилиндра; H — |
|
|
|
|
|
высота цилиндра;R — радиус осно- |
|
|
|
|
|
вания. |
|
|
|
|
|
Найти: I — момент инерции ци- |
|
|
|
|
|
линдра (диска). |
|
|
|
|
|
Так как ось проходит через центр симметрии цилиндра, то I = IC. |
|||||
По определению объем и плотность сплошного однородного цилин- |
|||||
дра |
|
|
|
|
|
V = SH = πR2 H , |
|
|
(1) |
||
|
ρ = m . |
|
|
|
(2) |
|
V |
|
|
|
|
Выделим бесконечно тонкий цилиндрический слой толщиной dr |
|||||
на расстоянии r от оси цилиндра. Объем и масса бесконечно тонко- |
|||||
го слоя равны |
|
|
|
|
|
dV = dsH = 2πrdrH , |
|
|
(3) |
||
dm = ρdV = m |
2πrHdr = m2πrHdr |
= 2mrdr . |
|
(4) |
|
V |
|
πR2 H |
R2 |
|
|
298 |
Глава 5. ЭЛЕМЕНТЫ МЕХАНИКИ ТВЕРДОГО ТЕЛА |
Здесь ds = 2πrdr — площадь заштрихованного кольца. Так как все точки бесконечно тонкого цилиндрического слоя находятся на одном и том же расстоянии r от оси, то бесконечно малый момент инерции этого слоя равен
dI = r2 dm = r2 |
2mrdr |
= |
2m |
r3dr . |
(5) |
R2 |
|
||||
|
|
R2 |
|
||
Момент инерции сплошного цилиндра относительно оси, проходящей через его центр параллельно направляющим, равен сумме моментов инерции относительно той же оси всех бесконечно тонких цилиндрических слоев, на которые можно разрезать сплошной цилиндр. Расстояние r от произвольного слоя до оси изменяется от 0 до R. Тогда получаем (5.37)
I = IC |
= |
∫ |
dI = |
R r2 dm = |
2m |
R r3dr = |
2m r4 |
|
|
R |
= m |
R4 |
= |
mR2 |
. (6) |
||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
R2 |
R2 4 |
|
|
|
2R2 |
||||||||||||
|
|
|
∫ |
∫ |
|
|
|
|
2 |
|
|||||||
|
|
|
|
0 |
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Так как результат не зависит от высоты цилиндра, то он справедлив и для любого диска радиусом R, массой m.
Ответ: IC = |
mR2 |
(для цилиндра и диска). |
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
Задача 5.7 |
|
|
|
|
|
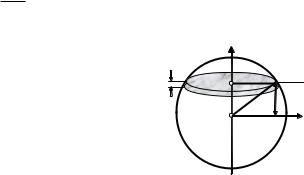
Определить момент инерции шара ра- |
|
Y |
|
||
диусом R и массой m относительно оси, |
dy |
x |
|
||
проходящей через его центр |
|
||||
|
|
|
|||
Дано: m — масса шара; R — радиус |
|
R |
y |
||
шара. |
|
|
|
||
|
|
|
C |
X |
|
Найти: I — момент инерции шара. Так как ось проходит через центр сим-
метрии шара, то I = IC. Направим оси x и y так, как показано на рисунке. Выделим
бесконечно тонкий диск, вырезаемый двумя параллельными плоскостями, отстоящими от центра шара C на расстоянии y и y + dy. Пренебрегая краевыми эффектами, будем считать, что бесконечно малый объем и бесконечно малая масса такого диска
dV = π x2 dy , |
(1) |
dm = ρ dV = ρπ x2 dy , |
(2) |
5.4. Вращение твердого тела вокруг неподвижной оси... |
299 |
где ρ — плотность шара, πx2 — площадь круга, радиусом x. В задаче 5.5 рассчитан момент инерции диска относительно этой же оси
I = |
mR2 |
, |
|
2 |
|||
|
|
где m и R — масса и радиус диска. Сделаем в этом выражении следующие замены:
I → dI , m → dm , R → x . |
(3) |
Тогда получаем выражения для момента инерции бесконечно тонкого диска, находящегося на расстоянии y от центра шара
dI = |
dmx2 |
. |
(4) |
|
2 |
||||
|
|
|
Момент инерции шара равен сумме моментов инерции бесконечно тонких дисков, на которые можно разбить шар, расстояния y от диска до центра шара изменяются от –R до R. Так как таких дисков — бесконечное множество, то вместо суммирования моментов инерции надо производить их интегрирование. Проинтегируем выражение (4)
с учетом равенства (2) и равенства (5) (см. рис.) |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 = R2 − y2 , |
|
|
|
|
|
|
|
|
|
(5) |
||||||||||||||
|
|
|
|
|
|
|
I = IC = ∫ dI = ∫ |
x2 dm |
|
= ∫R |
x2ρπx2 dy |
= |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
− R |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
= ∫R πρ |
(R2 |
− y2 )2 dy = |
πρ |
∫R (R4 − 2R2 y2 + y4 )dy = |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
− R |
2 |
|
|
|
|
|
|
2 |
|
− R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
= |
πρ |
( ∫R R4 dy − 2R2 ∫R y2 dy + ∫R |
y4 dy) = |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
− R |
|
|
|
|
|
-R |
|
|
|
|
|
|
− R |
|
|
|
|
|
|
|
|
|
|
|
||
|
= |
πρ [R4 (R − (− R)) − 2R2 |
( |
R3 |
− |
(− R)3 |
) + ( |
|
R5 |
− |
(− R)5 |
)] = |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
5 |
||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
5 |
|
|
|
|
|
|
|
|||||||
πρ |
|
5 |
|
|
4R5 |
|
|
|
2R5 |
|
|
πρ |
5 |
|
|
14R5 |
πρ 16R5 |
|
|
3 8R2 |
|||||||||||||||||
= 2 |
(2R |
|
− |
|
|
+ |
|
) = |
2 (2R |
|
|
− |
|
|
|
|
) = |
2 |
( |
|
|
) = πρ R |
|
|
= |
||||||||||||
|
3 |
|
5 |
|
|
|
15 |
|
15 |
|
15 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
= ρ( |
4 |
π R3 ) |
2R2 |
= |
2 |
mR2 , |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
4 |
|
|
|
|
|
3 |
5 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где m = ρ |
π R3 |
|
— масса шара. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
mR2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: IC = |
(для шара). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
300 |
Глава 5. ЭЛЕМЕНТЫ МЕХАНИКИ ТВЕРДОГО ТЕЛА |
||||
Задача 5.8 |
|
|
|
|
|
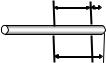
Определить момент инер- |
Ось вращения, проходящая |
Ось вращения |
|||
ции I тонкого однородно- |
через центр масс |
a |
b |
|
|
|
|||||
го стержня длиной L = 1 м и |
C |
|
|
|
|
|
|
|
|
||
массой m = 0,3 кг относитель- |
|
|
|
|
|
но оси, перпендикулярной |
|
L/2 |
|
|
|
стержню и проходящей через |
|
|
|
|
|
точку, отстоящую от конца стержня на b = L/10. |
|
|
|
|
|
Дано: m = 0,3 кг; L = 1 м; b = L/10 = 0,01 м. |
|
|
|
|
|
Найти: I. |
|
|
|
|
|
В задаче 5.4 вычислен момент инерции однородного стержня исходя из определения момента инерции. Рассмотрим эту же задачу с использованием теоремы Штейнера. По теореме (5.41) момент инер-
ции стержня относительно произвольной оси |
|
I = IC + ma2. |
(1) |
Центр масс стержня находится в центре его симметрии, т. е. в середине. Момент инерции стержня относительно оси, проходящей через его центр масс перпендикулярно стержню (задача 5.4, выражение 7)
IC |
= |
mL2 |
. |
(2) |
|
||||
|
12 |
|
|
|
Расстояние между осью вращения и параллельной ей осью вра-
щения, проходящей через центр масс стержня, |
|
|
|||||||||||||||||
|
|
|
a = |
L |
|
− b = |
L |
− |
|
L |
|
= 0, 4L . |
|
(3) |
|||||
|
|
|
|
2 |
10 |
|
|
||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
Подставляя (2) и (3) в (1), получаем |
|
|
|||||||||||||||||
|
I = IC + ma2 = |
mL2 |
|
+ m( |
2 |
L)2 = |
73 |
mL2 . |
(4) |
||||||||||
|
|
|
|
||||||||||||||||
|
|
|
12 |
|
|
|
5 |
300 |
|
|
|||||||||
Найдем численное значение момента инерции |
|
||||||||||||||||||
|
|
I |
73 |
|
0,3 12 = 0, 073 кг · м2. |
|
|
||||||||||||
|
|
= |
|
|
|
||||||||||||||
300 |
|
|
|||||||||||||||||
73 |
mL2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: I = |
|
= 0, 073 кг · м2. |
|
|
|
|
|
|
|
|
|||||||||
300 |
|
|
|
|
|
|
|
|
|||||||||||
Составим таблицу из полученных нами значений моментов инерции некоторых тел. Все рассмотренные тела являются фигурами вра-

 r
r