
fizika
.pdf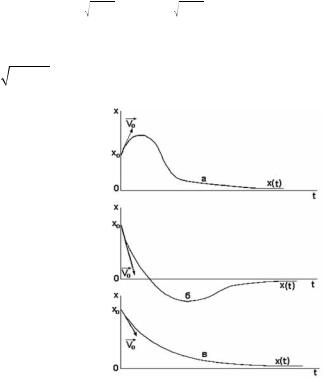
6.6. Затухающие механические колебания |
361 |
Тогда общее решение находится как линейная комбинация част-
ных решений
x(t) = C1 x1 + C2 x2
или
|
−β + |
β |
2 |
−ω |
2 |
|
|
|
−β − |
β |
2 |
−ω |
2 |
|
|
|
0 |
t |
+ C |
|
|
0 |
t |
||||||
x(t) = C e |
|
|
|
|
|
e |
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
где С1 и С2 — произвольные константы. |
|
|
|
|
|
|
||||||||
Проанализируем зависимость x (t). |
|
|
|
|
|
|
|
|||||||
Так как β > β2 − ω02 , то степенная функция со временем убывает. Характер убыванияG зависит от начальной координаты х0 и начальной скорости v0 . Возможные си-
туации приведены на рис. 6.12. ЕслиG х0 > 0, начальная скорость v0 направлена от положения равновесия, то зависимость
x (t) имеет вид а на рис. 6.12. ЕслиG х0 > 0, начальная ско-
рость v0 достаточно велика и направлена к положению равновесия, то груз один раз может пересечь положение равновесия, а затем устремиться к нему. Зависимость x (t) имеет вид б на рис. 6.12.
ЕслиG х0 > 0, начальная скорость v0 мала и направлена к положению равновесия, то зависимость x (t) имеет вид в на
рис. 6.12. |
Рис. 6.12 |
|
2 вариант
Если β = ω0 , то корни α1,2 = −β , т. е. корни α1 и α2 являются кратными. Частные решения одинаковы и равны eαt .
В этом случае, чтобы не потерять одно частное решение, вместо постоянных интегрирования С1 и С2, следует записать многочлен, степень которого на единицу меньше кратности корня характеристического уравнения. Общее решение запишется в виде
362 |
|
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
||
x(t) = C e−βt + C |
te−βt = e−βt (C + tC |
2 |
) . |
|
1 |
2 |
1 |
|
|
Поскольку многочлен (С1 + t C2) растет намного медленнее, чем убывает сомножитель e−βt , то функция x (t) будет близка к видам а, б, в, приведенным на рис. 6.12.
Вывод. При β ≥ ω0 движение груза перестает быть периодическим, т. е. система возвращается в равновесное состояние без колебательного процесса. Это может иметь место тогда, когда, например, сила сопротивления среды больше силы упругости пружины. Такой характер движения называют апеpиодическим затуханием.
3 вариант |
|
|
|
|
Если ω0 |
> β , то корни α1 и α2 комплексные и принимают значения |
|||
α |
2 |
= −β ± −1(ω02 |
− β2 ) = −β ± i |
(ω02 − β2 ) = −β ± iω , |
1, |
|
|
|
|
где i — мнимое число, ω = ω02 − β2 — циклическая частота затухающего колебания. Такая ситуация имеет место тогда, когда сила сопротивления среды меньше силы упругости пружины, т. е. Fупр > FR.
Каждому значению корня α1,2 соответствует частное решение. Общее решение находится как линейная комбинация двух частных решений:
x(t) = C*e(−β + iω)t |
+ C*e(−β −iω)t |
= C*e−βt eiωt + C*e−βt e−iωt = |
||||||||
1 |
2 |
|
1 |
|
|
|
|
|
2 |
|
= C1*e−βt (cos ωt + i sin ωt) + C2*e−βt (cos ωt − i sin ωt) = |
||||||||||
= e−βt cos ωt(C* + C |
* ) + sin ωt(iC* − iC* ) . |
|||||||||
|
1 |
2 |
|
|
|
|
1 |
|
2 |
|
Переобозначив константы C = C* + C* , |
|
C |
2 |
= iC* |
− iC* , получим |
|||||
|
1 |
1 |
|
2 |
|
|
1 |
2 |
||
x(t) = e−βt (C cos ωt + C |
2 |
sin ωt) . |
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
Так как C1 cos ωt + C2 sin ωt = A0 cos(ωt + ϕ0 ) |
(см. параграф 6.3.1), |
|||||||||
то |
|
|
|
|
|
|
|
|
|
|
x(t) = A e−βt cos(ωt + ϕ |
0 |
) . |
|
|
(6.40) |
|||||
|
0 |
|
|
|
|
|
|
|
|
|
Это и есть решение уравнения (6.39).
Собственные затухающие колебания маятника периодические, но не являются гармоническими, так как амплитуда таких колебаний с течением времени уменьшается по экспоненте
A = A e−βt , |
(6.41) |
0 |
|
где β — коэффициент затухания. |
|
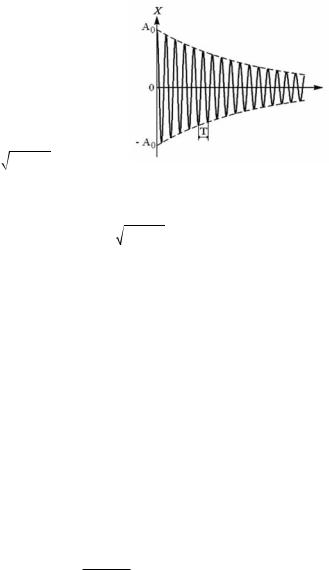
6.6. Затухающие механические колебания |
363 |
График затухающих колебаний x (t) показан на рис. 6.13. Зависимость x (t) не выходит за пределы
огибающих функций x = A0e−βt и x = − A0e−βt .
Циклическая частота затухающих колебаний ω связана с собственной частотой пружинного маятника ω0 соотношением
ω = ω02 − β2 . |
|
|
|
|
|
Рис. 6.13 |
Условный период затухающих |
|
|
||||
|
|
|
||||
колебаний равен |
|
|
|
|
|
|
T = |
2π |
= |
|
2π |
. |
(6.42) |
ω |
|
ω02 − β2 |
||||
|
|
|
|
|
||
Условный период затухающих колебаний — наименьший промежуток времени Т, за который колеблющийся груз дважды проходит через положения равновесия, двигаясь в одном и том же направлении. Период затухающих колебаний груза больше периода незатухающих колебаний этого же груза, так как силы сопротивления тормозят движение; тело возвращается к равновесному состоянию медленнее.
На рис. 6.13 сплошной линией показана зависимость x = x (t), штриховая линия проведена по максимальным значениям амплитуды затухающих колебаний.
Основные параметры, характеризующие затухающие колебания
Логарифмический декремент затухания — логарифм отношения двух амплитуд, смещенных по времени на один период
λ = ln |
A e−βt |
= βT . |
|
0 |
(6.43) |
||
A e−β(t +T ) |
|||
|
0 |
|
|
Время релаксации затухающих колебаний τ — время, в течение которого амплитуда колебаний уменьшается в e раз.
Из условия
A0e−(βt ) = e ,
A0e−β t + τ

6.6. Затухающие механические колебания |
365 |
Вопросы и задания для самопроверки
1.Как влияет коэффициент затухания на период затухающих колебаний?
2.Можно ли утверждать, что дифференциальное уравнение затухающих колебаний
d 2 x |
+ 2β |
dx |
+ ω2 x = 0 |
|
dt2 |
dt |
|||
|
0 |
есть иная форма записи второго закона Ньютона?
3.Циклическая частота затухающих колебаний ω больше или меньше собственной частоты ω0?
4.Нет ли ошибки в утверждении: «Время релаксации затухающих колебаний — время, в течение которого амплитуда колебаний уменьшается в 2,7 раза»?
5.Дайте определение коэффициента затухания β.
6.Дайте определение логарифмического декремента затухания λ.
7.Увеличивается или уменьшается период затухающих колебаний, если увеличивается сила сопротивление среды?
8.Увеличивается или уменьшается условный период затухающих колебаний при уменьшении коэффициента упругости пружинного маятника?
9.Будут ли происходить периодические колебания, если ω0 < β?
10.Величину, равную числу полных колебаний в единицу времени, называют частотой колебаний или циклической частотой?
Примеры решения задач
Задача 6.11
Затухающие колебания происходят по закону x = 10e−0,3t cos πt .
Найти амплитуду колебаний после n = 10 полных колебаний. Дано: x = 10e−0,3t cos πt ; n = 10.
Найти: A10.
Амплитуда затухающих колебаний уменьшается по экспоненциальному закону
A= A0e−βt .
Сучетом условия задачи уравнение примет вид

366 Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
A10 = 10e−0,3t .
Так как амплитуду колебаний следует найти по истечении t = 10T,
то
A10 = 10e−0,3 10T = 10e−3T .
Период колебания равен
T = 2ωπ = 2ππ = 2 c.
Ответ: амплитуда после десяти полных колебании равна
A10 = 10e−3 2 = 10e−6 = 0, 025 м.
Задача 6.12
Пружинный маятник, совершающий колебательное движение, теряет за период 9 % энергии. Сколько колебаний совершает маятник за время релаксации τ?
Дано: η = WW = 0, 09 .
Найти: N.
Уравнение затухающих колебаний имеет вид: x = A0e−βt cos(ωt + ϕ0 ) .
Чтобы найти число колебаний N за время релаксации τ, необходимо найти время релаксации. Время релаксации τ — время, в течение которого амплитуда колебаний уменьшается в e раз, связанные с периодом Т и числом N колебаний, совершаемых за время релаксации, соотношением τ = NT. Коэффициент затухания β связан с вре-
менем релаксации τ соотношением τ = β1 .
Полная энергия маятника в моменты времени t и t + T имеют вид:
W (t) = kA2 (t) ,
2
W (t + T ) = kA2 (t + T ) .
2
Амплитуды затухающих колебаний маятника в моменты времени t и t + T имеют вид:


368 |
|
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
||
|
A0 |
= e |
βt |
= n. |
|
|
1 |
||
|
A(t ) |
|||
|
|
|
|
|
1 |
|
|
|
|
Прологарифмируем полученное уравнение ln n = βt1 .
Расчетная формула для вычисления коэффициента затухания имеет вид
β = ln n t1 .
Ответ: коэффициент затухания пружинного маятника β = 0,23 c—1.
6.7. ВЫНУЖДЕННЫЕ МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Рассмотрим колебания на примере пружинного маятника (рис. 6.11), который периодически подвергается внешним воздействиям в виде толчков, направленных в одну и ту же сторону и повторяющихся через одинаковые промежутки времени. Переменную внешнюю силу, приложенную к телу на пружине и вызывающую механические колебания, называют возмущающей силой.G ПустьG возмущающая сила изменяется по гармоническому закону F = F0 sin Ωt , где F0, Ω — ам-
плитуда и циклическая частота возмущающей силы. Пусть на систе- |
||||||
му действуют сила тяжести mgG |
, сила упругости FG |
, сила сопротив- |
||||
ления среды FGR и возмущающая сила FG |
упр |
|
||||
= FG0 sin Ωt . |
|
|||||
Запишем второй закон Ньютона для груза |
|
|||||
G |
G |
G |
|
G |
G |
(6.44) |
mg |
+ F |
+ F |
|
+ F sin Ωt = ma . |
||
|
упр |
R |
0 |
|
|
|
Если повторить процедуры, проделанные в параграфе 6.6, с уче-
том возмущающей силы, получим: |
|
|
|
|
|
|||||||
|
m |
d 2 x |
= −kx − r |
dx |
+ F sin Ωt |
|
||||||
|
dt2 |
dt |
|
|
||||||||
или |
|
|
|
|
|
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 x |
|
dx |
+ ω02 x |
|
|
F |
sin Ωt. |
|
|||
|
|
|
+ |
2β |
|
= |
0 |
(6.45) |
||||
|
dt |
2 |
dt |
m |
||||||||
|
|
|
|
|
|
|
|
|
|
|||
Общее решение полученного неоднородного линейного дифференциального уравнения с постоянными коэффициентами (см. § 4.5 главы «Математическое введение») складывается из двух слагаемых:
6.7. Вынужденные механические колебания |
369 |
1) общего решения соответствующего однородного дифференци-
ального уравнения |
|
|
|
|
|
|
|
d 2 x |
+ 2β |
dx |
+ ω2 x = 0, |
|
|
|
dt2 |
|
|
|||
|
|
dt |
0 |
|
|
|
имеющего при ω0 > β вид: |
|
|
|
|
|
|
x (t) = A e−βt |
sin(ωt + ϕ |
0 |
), |
|||
1 |
0 |
|
|
|
||
2) частного решения неоднородного дифференциального урав-
нения |
|
|
|
|
|
|
|
d 2 x |
+ 2β |
dx |
+ ω2 x = |
F |
sin Ωt |
|
|
|
0 |
|||
|
dt2 |
dt |
m |
|||
|
|
0 |
|
|||
имеющего вид: |
|
|
|
|
|
|
x2 (t) = Asin (Ωt − θ),
Пояснение
При наличии вязкого сопротивления среды в линейных системах (линейными системами называются системы, содержащие производные и функции в первой степени) нет явления резонанса (о резонансе будет сказано позже). Поэтому частное решение x2(t) можно искать в виде правой части (6.45). Однако из-за наличия вязкого сопротивления среды, движение груза отстает по фазе на θ от возмущающей силы F. Вследствие этого частное решение неоднородного
дифференциального уравнения ищется не в в виде x(t) = Asin Ωt , а в виде x2 (t) = Asin(Ωt − θ) .
Общее решение уравнения (6.45) равно сумме двух решений
x(t) = x1 (t) + x2 (t)
или
x(t) = A0e−βt sin(ωt + ϕ0 ) + Asin(Ωt − θ).
Вынужденные колебания устанавливаются не сразу, так как груз одновременно совершает и собственные, и вынужденные колебания. Собственные колебания маятника x1(t) постепенно затухают. Остаются только вынужденные колебания с частотой возмущающейся силы Ω
x(t) = Asin(Ωt − θ) . |
(6.45а) |
Чтобы найти A и θ необходимо решение (6.45а) подставить (6.45). Однако возникают затруднения из-за того, что х(t) и правая часть (6.45) имеют разные фазы. Чтобы устранить затруднение, искусст-

370 Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
венно преобразуем правую часть (6.45) таким образом, чтобы фазы были одинаковые.
Пояснение к искусственному преобразованию
Распишем по формуле синус суммы двух углов
sin Ωt = sin(Ωt − θ + θ) = sin(Ωt − θ) cos θ + cos(Ωt − θ) sin θ . (6.45б)
Подставим решение (6.45а) в (6.45), при этом в правой части уравнения учтем преобразование (6.45б).
− AΩ2 sin(Ωt − θ) + 2βAΩ cos(Ωt − θ) + ω02 Asin(Ωt − θ) ≡
|
F0 |
(6.45в) |
|
≡ |
[sin(Ωt − θ) cos θ + cos(Ωt − θ)sin θ]. |
||
m |
|||
|
|
Так как (6.45в) есть тождество, то приравняв соответствующие коэффициенты при sin(Ωt − θ) и cos(Ωt − θ) , получим
+ A(−Ω2 + ω02 ) = |
F0 |
cos θ, |
|||
m |
|||||
|
F0 |
|
(6.45с) |
||
|
|
|
|||
2βAΩ = |
sin θ. |
|
|
||
m |
|
|
|||
|
|
|
|
||
Для определения амплитуды А вынужденных колебаний возведем обе части уравнения (6.45с) в квадрат, сложим и извлечем корень квадратный.
Так как амплитуда величина положительная, то оставим только
положительное значение корня |
|
|
|
|
|
|
|
|
|
A2 (ω2 − Ω2 )2 |
+ 4β2Ω2 |
= |
F |
2 |
|
||||
|
0 |
, |
|||||||
|
|
|
2 |
||||||
|
0 |
|
|
|
m |
|
|||
|
|
F0 |
|
|
|
|
|||
A = |
|
|
|
|
|
. |
(6.46) |
||
m (ω02 − Ω2 )2 |
+ 4β2Ω2 |
|
|||||||
Для определения сдвига фазы θ разделим второе уравнение на пер-
вое (6.45с), получим |
|
|
|
|
|
|
tgθ = |
|
2βΩ |
||
|
|
. |
|
||
Отсюда |
ω02 − Ω2 |
||||
|
θ = arctg |
2βΩ |
|||
|
|
. |
|||
|
ω02 − Ω2 |
||||
Таким образом, если внешняя возмущающая сила изменяется по гармоническому закону, то вынужденные колебания являются также гармоническими.
