
fizika
.pdf
6.3. Динамика механических гармонических колебаний |
|
|
|
|
|
|
|
341 |
|||||||||||||
vx |
= |
dx |
|
= Aω0 cos(ω0t + ϕ0 ) , |
|
|
|
|
|
||||||||||||
dt |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a |
|
= |
d 2 x |
|
= − Aω2 |
sin(ω |
t + ϕ |
|
) . |
|
|
|
|
||||||||
x |
dt2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
0 |
0 |
|
|
0 |
|
|
|
|
|
|
|||||
Кинетическая энергия груза |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
W |
= |
mv2 |
= |
mA2 |
ω2 |
|
cos2 (ω |
t + ϕ |
|
) , |
|
|
|
||||||||
|
|
|
|
|
0 |
|
0 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
K |
|
|
2 |
|
|
|
2 |
|
|
|
0 |
|
|
|
|
mω02 |
A2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
совершающего гармонические колебания, изменяется от 0 до |
|
|
. |
||||||||||||||||||
2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Циклическая частота колебаний кинетической энергии равна 2ω0 ,
так как |
|
|
|
|
|
1+ cos 2(ω0t + ϕ0 ) |
|
|
|
|
|||||
|
cos2 (ω0t + ϕ0 ) |
= |
. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
Потенциальная энергия груза |
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||
W = |
kx2 |
= |
mω2 x2 |
= |
|
mω2 |
A2 |
2 (ω |
t + ϕ |
|
|
|
|||
|
0 |
|
0 |
|
sin |
0 |
) |
, |
|||||||
|
|
|
|
|
|||||||||||
П |
|
2 |
|
2 |
|
2 |
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
совершающего гармонические колебания под действием силы упру-
|
|
|
|
|
|
|
mω02 A2 |
||||
гости пружины, периодически изменяется от 0 до |
|
|
|
с цикли- |
|||||||
|
2 |
|
|||||||||
ческой частотой 2ω0 . |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
Полная энергия груза |
|
|
|
|
|
|
|
|
|||
|
|
|
W = WК + WП = |
|
|
|
|
||||
|
mω2 |
A2 |
mω2 |
A2 |
mω2 |
A2 |
|||||
= |
|
|
cos2 (ω0t + ϕ0 ) + |
0 |
|
sin2 (ω0t + ϕ0 ) = |
0 |
|
(6.12) |
||
2 |
|
2 |
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|||
—величина постоянная.
Колебания любой физической величины, характеризующей мате-
матический маятник, включая смещение х груза, записанное в форме (6.11), называют собственными незатухающими колебаниями. Ве-
личины ω0 = |
k |
и T = 2π |
m |
называют собственной циклической |
|
m |
k |
||||
|
|
|
частотой и периодом колебаний маятника соответственно. Чем больше масса груза m и меньше коэффициент упругости k пружины, тем медленнее происходят колебания. Полная энергия колеблющегося груза остается постоянной, так как движение происходит без притока и без потерь энергии.

6.3. Динамика механических гармонических колебаний |
343 |
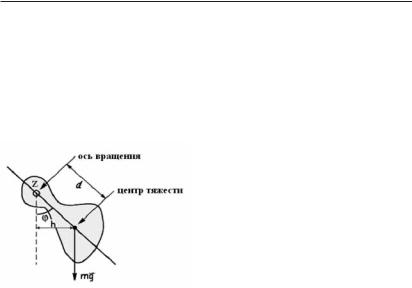
Дифференциальное уравнение движения физического маятника
(6.13) принимает вид |
|
|
|
|
|
−mgd sin ϕ = J |
|
d 2ϕ |
. |
(6.14) |
|
z |
dt2 |
||||
|
|
|
При малых углах ϕ функцию sinϕ можно разложить в степен-
ной ряд |
|
|
|
|
ϕ2n+1 |
|
|
|
|
sin ϕ = ϕ − |
ϕ3 |
+ |
ϕ5 |
− + (−1)n |
+ ... |
(6.15) |
|||
3! |
5! |
(2n + 1)! |
|||||||
|
|
|
|
|
|||||
Если ограничиться первым членом разложения (6.15) и обозначить
mgd = ω2 , Jz 0
то уравнение (6.14) примет вид
d 2ϕ |
2 |
|
|
|
|
+ ω |
ϕ = 0 . |
(6.16) |
|
dt2 |
||||
0 |
|
|
Уравнение (6.16) аналогично уравнению (6.9), следовательно, и решения уравнений одинаковы.
Таким образом, при малых углах ϕ колебательное движение физического маятника, как и колебательное движение пружинного маятника, является гармоническим, а именно
ϕ = ϕmax sin(ω0t + α0 ) . |
(6.17) |
где ϕmax — максимальное значение углового смещения маятника от положения равновесия, α0 — начальное значение фазы. Циклическая частота и период колебания физического маятника вычисляются соответственно по формулам
ω |
0 |
= |
mgd |
T = |
2π |
= 2π |
Jz |
. |
(6.18) |
Jz |
|
|
|||||||
|
|
|
ω0 |
mgd |
|
||||
При малых угловых смещениях период колебания маятника не зависит от амплитуды ϕmax и начальных условий движения.
Формулы (6.18) могут быть использованы для экспериментального нахождения момента инерции тел сложной формы относительно выбранной оси z.
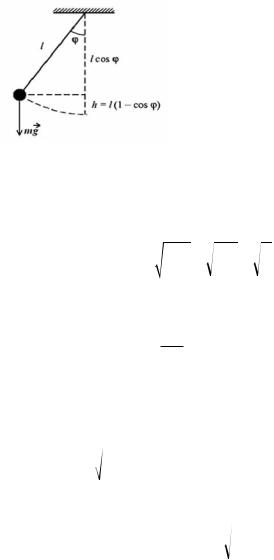
344 |
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
6.3.3. Математический маятник
Математический маятник — материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости под действием силы тяжести (рис. 6.5).
Математический маятник представляет собой предельный случай физического маятника, вся масса которого сосредоточена в точке. Тогда расстояние от точки приложения силы тяжести до
оси вращения равно длине нити l (рис. 6.5). Так как d = l, то момент инерции и циклическая частота такого маятника относительно оси вращения равны соответственно
Jz = ml2 ,
ω |
|
= |
mgd |
= |
mgl |
= |
g |
. |
(6.19) |
0 |
|
ml2 |
|
||||||
|
|
Jz |
|
l |
|
||||
Дифференциальное уравнение колебаний математического маятника при отсутствии сопротивления среды такое же, как и для физического маятника и имеет вид
d 2ϕ
dt2
Таким образом, при малых углах отклонения ϕ от вертикали движение математического маятника представляет собой гармоническое колебание, описываемое формулой (6.10)
ϕ = ϕmax sin(ω0t + α0 ) , |
(6.20) |
в которой ω0 = |
g |
. |
|
||
|
l |
|
Период колебаний математического маятника вычисляется по формуле
T = |
2π |
= 2π |
l |
. |
(6.21) |
|
|
||||
|
ω0 |
g |
|
||

6.3. Динамика механических гармонических колебаний |
345 |
Период колебаний не зависит от массы маятника m и амплитуды углового смещения ϕmax.
Математический маятник используется в технике. Например, в геологии по измеренным значениям Т и l вычисляют ускорение свободного падения для данной местности. Если в земной коре на исследуемой территории имеется неоднородность, то величина g отличается от стандартного значения. По этой аномалии можно предположить наличие полезных ископаемых.
Вопросы и задания для самопроверки
1.Как изменится частота, максимальная скорость, максимальное ускорение и полная механическая энергия гармонических колебаний, если удвоить амплитуду колебаний?
2.Два тела с одинаковыми массами подвешены к двум одинаковым пружинам. Тела оттягивают вниз — одно на 10 см, другое на 20 см —
изатем одновременно отпускают.
Какое из них первым пройдет положение равновесия?
3. Отличается ли максимальное значение кинетической энергии груза пружинного маятника от максимального значения потенциальной энергии деформированной пружины?
4. Отличается ли циклическая частота колебаний кинетической энергии от циклической частоты колебаний потенциальной энергий пружинного маятника?
5. Математический маятник длиной L = 1 м подвешен к потолку кабины, которая начинает опускаться вертикально с ускорением a = g4 . Определить период T малых колебаний маятника.
6.Какую длину должен иметь математический маятник, чтобы его период колебаний был равен одной секунде?
7.Докажите, что скорость математического маятника достигнет максимального значения, если его угловое смещение равно нулю.
8.Твердое тело закреплено таким образом, что ось вращения z проходит через точку приложения силы тяжести. Является ли это тело физическим маятником?
9.Период колебаний физического маятника тем больше, чем больше расстояние от точки приложения силы тяжести до оси вращения. Верно ли это утверждение?
346 |
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
Примеры решения задач
Задача 6.4
Рассказ Мюнхгаузена: «Как-то, гуляя, я невзначай забрался в горы. Захотелось узнать, на какой высоте я нахожусь. К счастью, в моей дорожной сумке оказались маятниковые часы. Держа их в правой руке неподвижно, я начал сравнивать ход механических часов с показаниями электронных часов на левой руке. За час маятниковые часы отстали от электронных на пять секунд, и я сразу понял, на какой высоте нахожусь». Вычислите эту высоту.
Примечание: Маятник часов сделан из такого сплава, что длина его от температуры не зависит. Электронные часы — точные. Радиус Земли примите равным R = 6400 км.
Дано: t = 1 ч = 3600 c; R = 6400 км = 6,4 · 106 м; t = 5 c. Найти: h.
Из второго закона Ньютона найдем ускорение свободного падения gh на высоте h над поверхностью Земли (на тело массой m действует только гравитационная сила)
G |
Mm |
= ma или gh = G |
M |
|
|
|
. |
||
(R + h)2 |
(R + h)2 |
|||
На поверхности Земли (h = 0) ускорение свободного падения равно
g = G RM2 .
Таким образом, при подъеме на высоту h ускорение свободного падения уменьшается
g |
= |
(R + h)2 GM |
= |
(R + h)2 |
. |
|||
|
|
|
|
|
||||
gh |
GM R2 |
R2 |
||||||
|
|
|
||||||
Период колебаний маятниковых часов на поверхности Земли и на высоте h равны соответственно
|
|
T = 2π |
|
l |
и T = 2π |
l |
, |
|
||||||
|
|
|
|
|
|
|
g |
|
h |
|
|
gh |
|
|
а их отношение |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
T |
|
= |
g |
h |
= |
|
R2 |
= |
|
R |
, |
||
|
T |
|
g |
|
(R + h)2 |
|
R + h |
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
h |
|
|
|
|
|
|
|
|
|
|
|
||

6.3. Динамика механических гармонических колебаний |
347 |
где
= T (R + h) Th R .
Так как при подъеме на высоту h ускорение свободного падения уменьшается, то период колебаний маятника на высоте h увеличится на T
T = T − T = |
T (R + h) |
− T = T |
h |
. |
|
|
|||
h |
R |
|
R |
|
|
|
|||
Если за одно колебание на высоте h период T увеличивается на T, то за время t, равное 3600 с, на этой же высоте суммарный пери-
од колебания увеличится на |
t, т. е. |
|
|
|
|||||
|
t |
= |
T |
|
т. е. |
|
t = |
th |
|
|
t |
T |
R |
||||||
|
|
|
|
|
|
||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
h = |
|
R |
t |
. |
||
|
|
|
|
t |
|
||||
|
|
|
|
|
|
|
|
|
|
Ответ: высота, на которую поднялся Мюнхгаузена, равна 8889 м. Примечание: Полученная высота чуть больше высоты Джамалунгмы (8848 м) — самой высокой вершины на Земле. Сомнений в правильности расчетов не должно быть, поскольку при решении были
приняты допущения t = T.
Задача 6.5
Насколько будут отставать за сутки часы с секундным маятником, если их перенести из подвала на верхний этаж здания? Расстояние между ними — 200 м.
Дано: h = 200 м; tc = 24 · 3600 = 8,64 · 104 с. Найти: t.
Маятник часов за сутки должен совершить N = tc колебаний,
T1
где T1 — период колебаний маятника в подвале. Если период колебаний маятника на верхнем этаже обозначить Т2, то за сутки часы отстанут на
t = N (T2 − T1 ) .
Периоды колебания часов до и после переноса равны

348 |
|
|
|
|
|
|
|
|
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
||||||||
T = 2π |
A |
, T = 2π |
A |
. |
|
||||||||||||
|
|
|
|||||||||||||||
|
1 |
|
|
|
|
g1 |
|
2 |
|
|
|
g2 |
|
|
|||
Отношение периодов |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
T1 |
|
= |
|
g2 |
. |
|
|
|
|
|
|||
|
|
|
|
T |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
g |
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|||
Из закона всемирного тяготения следует, что |
|||||||||||||||||
|
|
|
g2 |
|
= |
|
R |
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|||
|
|
|
g |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
R + h |
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где R — радиус Земли. Отсюда следует, что |
|
|
|||||||||||||||
T = T |
R + h |
и |
t = N (T − T ) = |
Nh |
T . |
||||||||||||
R |
|
||||||||||||||||
2 1 |
|
|
|
|
|
|
2 |
1 |
|
R 1 |
|||||||
Ответ: отставание часов за сутки при переносе их с подвала на верхний этаж 2,7 с.
Задача 6.6
Амплитуда гармонических колебаний груза пружинного маятника А = 2 см, полная энергия W = 0,3 мкДж. При каком смещении груза х от положения равновесия на груз действует сила F = 22,5 мкН?
Дано: A = 2 см = 0,02 м; W = 0,3 мкДж = 3 · 10–7 Дж; F = 22,5 мкН = 2,25 · 10–7 Н.
Найти: х.
Запишем уравнение гармонических колебаний точки в общем
виде
x = Asin(ω0t + ϕ0 ) .
Найдем скорость точки, взяв производную от функции х(t) по времени
vx = dxdt = Aω0 cos(ω0t + ϕ0 ) .
Полная энергия системы, равна сумме потенциальной и кинетической энергий
W = |
kx2 |
+ |
mv2 |
= |
kA2 |
sin2 |
(ω0t + ϕ0 ) + |
mA2 |
ω2 |
cos2 (ω0t + ϕ0 ) . |
|||
|
x |
|
|
|
|
0 |
|||||||
2 |
2 |
2 |
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|||||
Учитывая, что ω02 |
= |
k |
|
, получим |
|
|
|
||||||
m |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
6.3. Динамика механических гармонических колебаний |
349 |
||||||
W = |
kA2 |
sin2 (ω0t + ϕ0 ) + |
mA2 k |
cos2 |
(ω0t + ϕ0 ) = |
kA2 |
. |
|
|
|
|||||
2 |
|
2m |
2 |
|
|||
Коэффициент упругости пружины находится через полную энергию и амплитуду колебания
k = 2E . A2
Модуль квазиупругой силы, дeйствующей на груз в процессе колебаний, равен
F = kx или F = 2AE2 x .
Ответ: смещение груза х от положения равновесия при действии силы F = 22,5 мкН равно
=FA2 =
x1,5 см.
2E
Задача 6.7
Однородный диск радиуса R колеблется около горизонтальной оси, перпендикулярной плоскости диска и проходящей на расстоянии d от центра диска. Каков период его колебаний?
Дано: R.
Найти: T.
Период колебаний физического маятника
T = 2π |
I |
, |
mgd |
где d — расстояние от оси вращения до точки приложения силы тяжести. Согласно теореме Штейнера момент инерции I относительно оси, не проходящей через цент тяжести диска,
I = I0 + mA2 ,
где I0 — момент инерции диска относительно оси, проходящей через центр тяжести; m — масса диска; A — расстояние между осями, равно d.
Учитывая, что I = 12 mR2 , получим
I = 12 mR2 + md 2 .

350 |
|
|
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
Ответ: период колебания физического маятника равен |
|||
1 |
R2 + d 2 |
|
|
T = 2π |
2 |
|
. |
|
gd 2 |
||
|
|
|
|
Задача 6.8
Ареометр, имеющий форму цилиндрической трубки, массой m и с поперечным смещением S, помещенный в жидкость с плотностью ρ, совершает свободные колебания около положения равновесия. Вычислить период колебания ареометра.
Дано: m; S; ρ. Найти: Т.
Ареометр — прибор для измерения плотности жидкости. Ось цилиндрической трубки ареометра перпендикулярнаGее поверхности. На плавающий ареометрGдействует сила тяжести mg , направленная вниз, и сила Архимеда FA , направленная вертикально вверх. В положении равновесия
mg = ρgSh ,
где Sh — объем погруженной части прибора.
Если погрузить ареометр на глубину h + x, то условие равновесия нарушится и, на ареометр будет действовать результирующая сила
F = ρgSh + ρgSx − mg = ρgSx .
Так как ρ, g, S — константы, то F = kx, где k = ρgS. Результирующая сила, действующая на ареометр, подобна упругой силе, действующей груз, висящий на пружине. Силы, не являющиеся упругими по своей природе, но подобные упругим силам по характеру зависимости от координаты, называются квазиупругими. Под действием квазиупругой силы движение ареометра описывается такими же уравнениями, как и пружинный маятник. Следовательно, период колебания ареометра можно вычислить по формуле
T = 2π |
m |
= 2π |
m |
. |
|
|
k |
|
|
|
|||
|
|
sρg |
|
|
||
Ответ: период колебания ареометра T = 2π |
m |
. |
||||
|
||||||
|
|
|
|
|
sρg |
|
