2.6.4.Сила вязкого трения и сопротивления среды.

Сила вязкого трениявозникает между слоями одного и того же сплошного тела (жидкости или газа). Сила вязкого трения за­висят от относительной скорости смещения отдельных слоев газа или жидкости друг относительно друга. Например, вязкое трение возникает при течении жидкости или газа по трубам со скоростью(рис. 2.3).

Скорость слоев жидкости уменьшается при приближении их к стенкам трубы. Отношение разности скоростей в двух близких слоях, расположенных на расстоянии, называется средним градиентом скорости.

В соответствии с уравнением Ньютона модуль средней силы вязкого трения

(2.54)

где –коэффициент вязкости,S– площадь взаимодействующих слоев среды, расположенных на расстоянии ∆xдруг от друга.

Коэффициент вязкости зависит от агрегатного состояния и температуры вещества.

Коэффициент вязкости

Вещество	Вода	Водяной пар	Машинное масло	Воздух
t0C	20	100	30	20
	1,0	0,013	200	0,018

Сила сопротивления возникает при движении твердых тел в жидкости или газе. Модуль силы сопротивления пропорционален плотности среды, площади поперечного сечения движущегося телаSи квадрату его скорости

, (2.55)

где[кг/м] – коэффициент сопротивления среды.

Тело, движущееся в среде испытывает действие силы вязкого трения (F_тр) и силы сопротивления (F_сопр). При небольших скоростях сила сопротивления меньше силы вязкого трения, а при больших – значительно превосходит ее (рис. 2.4).

При некотором значении скорости силыF_триF_сопрстановятся равными по модулю.

Сила сопротивления среды зависит от формы движущегося тела. Форму тела, при которой сила сопротивления мала, называют обтекаемой. Ракетам, самолетам, автомобилям и другим машинам, движущимся с большими скоростями в воздухе или в воде, придают обтекаемую, каплеобразную форму

2.6.5.Сила упругости. Закон Гука.

П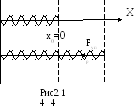ри действии на тело внешних сил, возникает упругая и неупругая деформация.

П

x

x₀=0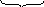

ри упругой деформации тело после прекращения действия внешних сил полностью восстанавливает свою форму и размеры. При неупругой деформации форма и размеры тела не восстанавливаются.

Упругая деформация пружины.

При растяжении пружины (рис 2.14) на величину относительно её равновесного состояния (х₀= 0) возникает упругая сила, которая возвращает пружину в прежнее положение после прекращения действия внешней силы. Модуль упругой силы, возникающей при линейном растяжении или сжатии пружины определяется законом Гука.

, (2.56)

где – проекция силы упругости на осьx, знак минус учитывает противоположные направления силыи перемещения пружины.

Деформация стержня

Стержень длинной l₀ и сечениемSпри действии силиперпендикулярно его торцам в противоположных направлениях деформируется (растягивается или сжимается) (рис 2.15). Деформация стержня определяется относительной величиной

(2.57)

где ∆l =l - l₀ , l-длинна стержня после деформации.

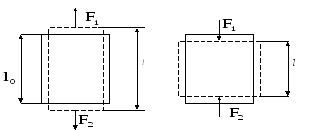
Рис. 2.15

Опыт показывает, что

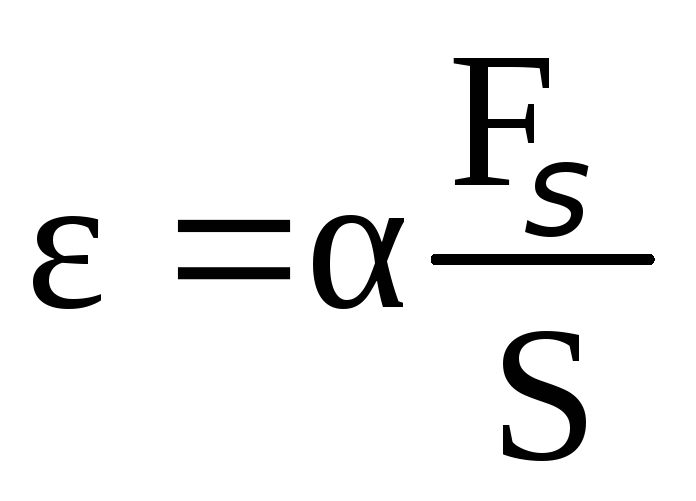, (2.58)

где α – коэффициент упругости стержня,

=σ – нормальное напряжение, измеряемое в(паскаль).

Наряду с коэффициентом упругости aдля характеристики упругих свойств тел при нормальных напряжениях используютмодуль ЮнгаЕ = 1/a, который, как и напряжение, измеряется в паскалях.

Относительное удлинение (сжатие) и модуль Юнга в соответствии с равенствами (2.13 и 2.14) определяется из соотношений:

,. (2.59)

Модуль Юнга равен такому нормальному напряжению, при котором деформация стержня Dlравна его первоначальной длинеl₀. В действительности при таких напряжениях происходит разрушение стержня.

Решая уравнение (2.58) относительно F, и подставляя вместоe=Dl/l₀,a= 1/Е, получим формулу для определения силы деформирующей стержень с сечениемSна величину

, (2.60)

где – постоянный для стержня коэффициент, который в соответствии с законом Гука соответствует коэффициенту упругости стержня при его сжатии и растяжении.

При действии на стержень касательного (тангенциального) напряжения

силы F₁ иF₂приложены параллельно противоположным граням площадьюSпрямоугольного стержня вызываютдеформацию сдвига (рис 2.16).

b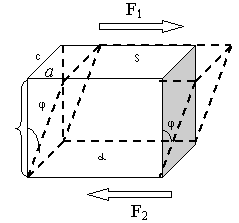

Рис. 2.16

Если действие сил равномерно распределено по всей поверхности соответствующей грани, то в любом сечении, параллельном этим граням, возникает тангенциальное напряжение . Под действием напряжений тело деформируется так, что одна грань сместиться относительно другой на некоторое расстояниеа. Если тело мысленно разбить на элементарные, параллельные рассматриваем граням слои, то каждый слой окажется сдвинутым относительно соседних с ним слоев.

При деформации сдвига любая прямая, первоначально перпендикулярная к слоям, отклонится на некоторый угол φ. тангенс которого называется относительным сдвигом

, (2.61)

где b– высота грани. При упругих деформациях угол φ очень мал, поэтому можно считать, чтои.

Опыт показывает, что относительный сдвиг пропорционален тангенциальному напряжению

, (2.62)

где G– модуль сдвига.

Модуль сдвига зависит только от свойств материала и равен тангенциальному напряжению при угле φ = 45˚. Модуль сдвига так же, как и модуль Юнга измеряется в паскалях (Па). Сдвиг стержня на уголвызывает сила

=GSφ, (2.63)

где G·S– коэффициент упругости стержня при деформации сдвига.