
методичка 2 семестр интегралы
.pdfНаціональний технічний університет України «Київський політехнічний інститут»
І. В. Алєксєєва, В. О. Гайдей, О. О. Диховичний, Л. Б. Федорова
ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ КІЛЬКОХ ЗМІННИХ.
ВИЗНАЧЕНІ ІНТЕГРАЛИ. ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ
ПРАКТИКУМ
Київ — 2011
Диференціальне числення функцій кількох змінних. Визначені інтеграли. Диференціальні рівняння. Практикум. (І курс ІІ семестр) / Уклад.: І. В. Алєксєєва, В. О. Гайдей, О. О. Диховичний, Л. Б. Федорова. — К: НТУУ «КПІ», 2011. — 184 с.
Гриф надано Методичною радою НТУУ «КПІ» (протокол № 6 від 18.02.2010)
Навчальне видання
Диференціальне числення функцій кількох змінних. Визначені інтеграли. Диференціальні рівняння.
Практикум
для студентів І курсу технічних спеціальностей
Укладачі: Алєксєєва Ірина Віталіївна, канд. фіз-мат. наук, доц.
Гайдей Віктор Олександрович, канд. фіз-мат. наук Диховичний Олександр Олександрович, канд. фіз-мат. наук, доц. Федорова Лідія Борисівна, канд. фіз-мат. наук, доц.
Відповідальний В. В. Булдигін, д-р фіз.-мат. наук, професор редактор Рецензенти: С. В. Єфіменко, канд. фіз.-мат. наук, доц.
В. Г. Шпортюк, канд. фіз.-мат. наук, доц.
Зміст
Вступ............................................................................................................................................. |
4 |
Довідник
Розділ 1. |
Диференціальне числення функцій кількох змінних |
................................... 5 |
Розділ 2. |
Визначені інтеграли ............................................................................................. |
16 |
Розділ 3. |
Диференціальні рівняння................................................................................... |
40 |
Практикум
Розділ 1. Диференціальне числення функцій кількох змінних
1. Функції кількох змінних ......................................................................................................... |
49 |
||
2. |
Похідні й диференціали функцій кількох змінних ................................................................ |
54 |
|
3. |
Дотична й нормаль до поверхні. Градієнт ............................................................................. |
61 |
|
4. |
Екстремуми функції кількох змінних..................................................................................... |
67 |
|
Розділ 2. Визначені інтеграли |
|
||
5. |
Обчислення визначеного інтеграла ........................................................................................ |
75 |
|
6. |
Застосування визначеного інтеграла ...................................................................................... |
81 |
|
7. |
Обчислення і дослідження невластивих інтегралів ............................................................... |
88 |
|
8. |
Подвійний інтеграл у декартових координатах ..................................................................... |
93 |
|
9. |
Заміна змінних у подвійному інтегралі................................................................................ |
100 |
|
10. |
Застосування подвійного інтеграла .................................................................................... |
104 |
|
11. |
Потрійний інтеграл ............................................................................................................. |
109 |
|
12. |
Криволінійний інтеграл 1-го роду...................................................................................... |
119 |
|
13. |
Обчислення криволінійного інтеграла 2-го роду............................................................... |
125 |
|
14. |
Застосування криволінійного інтеграла 2-го роду............................................................. |
130 |
|
15. |
Поверхневий інтеграл 1-го роду......................................................................................... |
134 |
|
16. |
Поверхневий інтеграл 2-го роду......................................................................................... |
139 |
|
17. |
Теорія поля .......................................................................................................................... |
143 |
|
Розділ 3. Диференціальні рівняння |
|
||
18. |
Диференціальні рівняння з відокремлюваними змінним .................................................. |
151 |
|
19. |
Однорідні диференціальні рівняння................................................................................... |
154 |
|
20. |
Лінійні диференціальні рівняння 1-го порядку. Рівняння Бернуллі ................................. |
158 |
|
21. |
Рівняння, що дозволяють пониження порядку .................................................................. |
163 |
|
22. |
Лінійні однорідні диференціальні рівняння із сталими коефіцієнтами............................ |
166 |
|
23. |
Лінійні неоднорідні диференціальні рівняння із сталими коефіцієнтами ........................ |
169 |
|
24. |
Системи лінійних диференціальних рівнянь ..................................................................... |
175 |
|
Додаток ................................................................................................................................... |
179 |
||
Список літератури................................................................................................................. |
184 |
||
Вступ
Практикум з вищої математики «Диференціальне числення функцій кількох змінних. Визначені інтеграли. Диференціальні рівняння» є складовою навчального комплекту з вищої математики, який становлять: конспект лекцій, практикум, розрахунково-графічна робота, збірник контрольних та тестових завдань.
Матеріал практикуму складено на основі багаторічного досвіду викладання математики авторами в НТУУ «КПІ», він відповідає навчальним програмам з вищої математики всіх технічних спеціальностей НТУУ «КПІ» денної та заочної форм навчання та містить наступні розділи дисципліни «Вища математика»:
—диференціальне числення функцій кількох змінних;
—визначені і невластиві інтеграли;
—невластиві інтеграли;
—кратні інтеграли;
—криволінійні інтеграли 1-го і 2-го роду;
—поверхневі інтеграли 1-го і 2-го роду;
—елементи теорії поля;
—диференціальні рівняння 1-го порядку, які інтегруються у квадратурах і рівняння вищих порядків які зводять до них;
—лінійні диференціальні рівняння зі сталими коефіцієнтами.
Практикум містить розгорнутий довідковий матеріал, широкий спектр розв’язаних навчальних задач, які достатньо розкривають відповідні теоретичні питання та сприяють розвиткові практичних навичок і є зразком належного оформлення задач для самостійної роботи, певну кількість задач для самостійної роботи в аудиторії та домашнього завдання.
Метою практикуму є:
допомогти в опануванні студентами основ математичного апарату у галузі диференціального числення функцій кількох змінних, усіх типів визначених інтегралів, теорії поля, диференціальних рівнянь;
розвинути логічне та аналітичне мислення;
виробити навички самостійної постановки задач та вибору методу їх
розв’язання; Самостійне розв’язання задач, яке формує основу математичного мислен-
ня, передбачає активну роботу з теоретичним матеріалом практикуму, використанням конспекту лекцій чи підручників.
У практичній частині використано такі позначення:
[A.B.C] — посилання на клітинку С, у якій вміщено теоретичний факт або формулу, таблиці A.B. з теми А;
,,,... — посилання у навчальній задачі на коментар, який вміщено після розв’язання.
Розділ 1. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ КІЛЬКОХ ЗМІННИХ
1.1. Функція двох змінних
Віддаль між точками |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
M (x |
;y ), M |
(x |
;y ) |
|
(M , M |
) (x |
2 |
x |
)2 (y |
2 |
y )2 |
||||||||||||||
1 |
1 |
1 |
|
2 |
2 |
2 |
|
1 |
2 |
|
|
|
|
1 |
|
|
|
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
M |
(x |
;...; x |
|
), M |
(x ;...; x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||||||
1 |
1 |
|
|
2 |
1 |
n |
(M1, M2 ) |
|
(xi |
xi )2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||||||||||||||||
-окіл точки M0 |
|
U (M0 ) {M n | (M, M0 ) } |
|||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
Класифікація точок. Точку |
Область. Множину D називають |
||||||||||||||||||||||||
M D називають внутрішньою |
відкритою, якщо всі її точки |
|
|
|
|
||||||||||||||||||||
точкою множини D, якщо існує такий |
внутрішні. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
U (M), що U (M) D. |
|
Множину D називають зв’язною, якщо |
|||||||||||||||||||||||
Точку M називають межовою точкою |
будь-які її точки можна сполучити |
||||||||||||||||||||||||
множини D, якщо будь-який U (M) |
ламаною L D. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Відкриту, зв’язну множину називають |
|||||||||||||||||||||||||
містить як точки, які належать D, так і |
|||||||||||||||||||||||||
точки, які їй не належать. |
областю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Об’єднання області D з її межею |
|||||||||||||||||||||||||
Множина всіх межових точок |
|||||||||||||||||||||||||
називають замкненою областю |
|
|
|
||||||||||||||||||||||
множини D утворює її межу D. |
|
|
|
||||||||||||||||||||||
|
|
|
|
D D. |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Функція двох змінних. Якщо |
|
y |
|
D |
|
|
|
f |
|
|
|
|
|
|
|
||||||||||
вказано правило f, за яким кожній |
|
y |
|
|
M |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
точці M(x;y) D 2 |
відповідає |
|
O |
|
x x |
|
|
|
E |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|||||||
єдине значення z E 1, то |
|
|
|
|
z |
|
|
|
|
|
|||||||||||||||
D — область означення; |
|
|
|
|
|
|
|||||||||||||||||||
кажуть, що в області D означено |
|
|
|
|
|
|
|||||||||||||||||||
E — множина значень |
|
|
|
|
|
|
|
||||||||||||||||||
функцію двох змінних |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
z f (x, y), (x;y) D 2. |
|
|
|
z |
|
|
|
Gf |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Графіком функції z f (x, y) |
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
називають |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||
Gf {M(x;y; z) 3 | z f (x, y)} |
|
|
|
|
|
D |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
Розділ 1. Диференціальне числення функцій кількох змінних |
|
||
|
|
|
|
|
|
|
Функція n змінних |
|
u f (x1, x2, ..., xn ) |
|
|
|
|
|
|
|
|
|
Лінія рівня функції z f (x, y) |
|
z |
|
|
|
|
LC {M(x;y) | f (x,y) C}, |
|
|
|
|
|
C const |
|
O |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
Поверхня рівня функції |
C |
{M(x;y;z) | f(x,y,z) C}, |
|
|
|
|
u f (x, y, z) |
|
C const |
|
|
|
|
|
|
|
1.2. Границя функції. Неперервність
Границя функції. |
|
0 ( ) 0 |
|||||
|
|
lim |
|
f (M ) A |
M U (M0 ) \ {M0} |
||
|
|
M M0 |
|
|
f (M ) U (A) |
||
|
|
|
|
|
|
||
|
|
|
|
|
Границя функції не залежить від |
||
|
|
|
|
|
напряму руху точки M до точки M0. |
||
|
|
||||||
Неперервність функції. |
вона визначена в околі точки M0 і |
||||||
Функцію u f (M ) називають |
|
lim f (M ) f (M0 ) |
|||||
неперервною в точці M0, якщо |
|||||||
|
M M0 |
||||||
|
|
||||||
Функцію, неперервну в кожній точці множини D, |
називають неперервною на |
||||||
множині D. |
|
|
|
|
|||
|
|
||||||
Частинні прирости функції |
xz(M0) f(x0 x, y0) f (x0, y0 ), |
||||||
z f(x, y) у точці M0 (x0 ; y0 ) |
yz(M0) f (x0, y0 y) f (x0, y0), |
||||||
|
|
|
|
|
де x x x0, y y y0 |
||
|
|
||||||
u f (x1, x2, ..., xn ) у точці |
xk u(M ) f (x1, ..., xk xk , ..., xn ) |
||||||
M(x |
; ...; x |
;...; x |
n |
) |
f (x1, ..., xk , ..., xn ) |
||
1 |
k |
|
|
|
|
||
|
|
|
|||||
Повний приріст функції |
|
z(M0 ) |
|||||
z f(x, y) у точці M0 (x0 ; y0 ) |
f (x0 |
x, y0 y) f(x0, y0 ) |
|||||
|
|
||||||
u f (x1, x2, ..., xn ) у точці |
u(M ) f (x1 x1, ..., xn xn ) |
||||||
M(x1; x2; ...; xn ) |
|
|
|
f (x1, ..., xn ) |
|||
|
|
|
|
|
|
|
|

|
Розділ 1. Диференціальне числення функцій кількох змінних |
7 |
|
|||
|
|
|
|
|
|
|
|
Умова неперервності функції |
lim u(M0 ) 0 |
|
|
||
|
u f (M ) у точці M0 |
M M0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема Веєрштраса. Якщо |
|
|
; |
|
|
|
1) u f(M) обмежена в області D |
|
|
|||
|
функція u f(M) неперервна в |
|
|
|
|
|
2) u f(M) набуває в області D
обмеженій замкненій області D, то:
своїх найбільшого та найменшого значень.
1.3. Похідні функцій кількох змінних
Частинна похідна функції |
z |
|
|
|
|
|
|
|
zx |
(M0 ) |
lim |
|
|
xz(M0 ) |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
z f (x, y) за змінною x у точці M0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||||||||||||||||||||||||||||||
|
|
|
M |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
z f (x, y) за змінною y у точці M0 |
z |
|
|
|
|
|
|
|
z |
(M |
0 |
) |
lim |
|
|
yz(M0 ) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
y 0 |
y |
|||||||||||||||||||||
|
|
|
|
|
|
M |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
u f(x1, ..., xn ) за змінною xk , |
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
u |
(M |
) |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
k 1, n, у точці M0 |
|
|
|
|
|
|
|
xk |
|
M0 |
|
|
|
|
|
|
x |
k |
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk u(M0 ) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
lim |
|
|
1, n |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, k |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
xk 0 |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Похідна складеної функції |
|
|
|
|
|
|
|
dz z dx z dy |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
z f (x, y), x x(t), y y(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
x dt |
|
|
|
|
y dt |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
u f(x1, ..., xn ), |
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
n |
|
|
u dxi |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x1 x1(t), ..., xn xn(t) |
|
|
|
|
|
|
|
|
|
|
dt |
|
xi |
|
|
dt |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z f (x, y), |
|
|
|
|
|
|
z |
|
|
|
z x |
|
|
z y |
, |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
x x(u, v), y y(u, v) |
|
|
|
|
|
u |
|
|
|
|
|
|
|
x u |
|
|
|
|
y u |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
z |
|
z x |
|
|
z y |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
x v |
|
|
|
y v |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
u f(x1, x2, ..., xn ), |
|
|
|
|
u |
|
|
|
|
|
n |
u x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
, j 1, m |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
t |
|
|
x |
t |
||||||||||||||||||||||||||||||||||
xi i(t1, ..., tm ),i 1, n |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
j |
|
|
i 1 |
|
|
|
i |
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Повна похідна функції |
|
|
|
|
|
|
|
|
dz |
z z dy |
|
|
|
|
|
||||||||||||||||||||||||||||||||
z f (x, y), y y(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
dx |
|
|
x |
|
|
|
y dx |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
8 |
|
|
Розділ 1. Диференціальне числення функцій кількох змінних |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Похідна неявної функції |
|
|
|
|
dy |
|
|
|
F |
(x, y) |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||
|
F(x, y) 0, |
|
y y(x) |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
F |
(x, y) |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (x, y, z) |
|
||||
|
F(x, y, z) 0, |
|
z z(x, y) |
|
|
Fx (x, y, z) |
, |
z |
|
y |
|
|
|||||||||||||||||||||||
|
|
|
x |
F (x, y, z) |
F (x, y, z) |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Похідні 2-го порядку функції z |
f (x, y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2z |
|
|
|
|
|
|
z |
|
|
|
2z |
|
|
|
|
|
|
|
|
|
|
z |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
; |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2 |
z |
2 |
|
|
|
; |
|
|
|
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
x |
|
|
|
|
|
|
|
|
|
|
x y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
x x |
|
|
|
|
|
|
|
|
|
|
y |
x |
|
|||||||||||||||
|
2 |
|
|
|
|
|
|
|
z |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|||||||
|
z |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
2 |
z |
|
2 |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
yx |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
y |
|
|
|
|
|
|
|
|
|
y x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
|
||||||||||||
|
|
|
|
|
|
y |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мішані похідні |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
Теорема Шварца. Нехай функція |
Якщо zxy |
та |
|
zyx |
неперервні в точці |
|
||||||||||||||||||||||||||||
|
z f (x, y) |
та її похідні zx , zy , zxy |
, zyx |
M0 |
D, |
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
означені в області D. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
z (M |
|
) z (M |
|
|
). |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xy |
|
|
|
|
|
yx |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.4. Диференціали функцій кількох змінних
Диференційовність функції |
z(M0 ) A x B y o( ), |
||||||
в точці. Функцію z f (x, y) |
|
0 |
|
|
|
|
|
називають диференційовною в точці |
|
|
|
|
|
||
де A, B const; |
|
|
|
|
|||
M0(x0;y0 ), якщо в деякому околі цієї |
|
|
|
|
|||
|
|
|
|
|
o( ) |
|
|
точки повний приріст функції має |
|
|
|
lim |
0 |
||
|
x2 y2 , |
||||||
вигляд |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
Функція u f (M ) диференційовна у |
|
n |
|
|
|
|
|
n |
u(M0 ) Ai xi |
o( ) |
|||||
точці M0 , якщо |
|
i 1 |
|
|
|
|
|
Необхідна умова |
Достатня умова |
|
|
|
|
||
диференційовності. Якщо функція |
диференційовності. Якщо функція |
||||||
z f (x, y) диференційовна в точці |
z f (x, y) має в околі точки M0 |
||||||
M0, то |
неперервні похідні zx (M ), zy(M ), то |
||||||
A zx (M0 ), B zy(M0 ). |
вона диференційовна в точці M0. |
||||||
|
|
|
|
|
|
|
|
|
Розділ 1. Диференціальне числення функцій кількох змінних |
|
9 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Повний диференціал функції |
повним диференціалом функції в точці |
|
||||||||||||||||||
|
в точці. Головну лінійну частину |
M0 і позначають du(M0 ): |
|
|
|
|
|||||||||||||||
|
приросту диференційовної в точці M0 |
u(M0 ) du(M |
0 ) o( ), 0 |
|
|||||||||||||||||
|
функції u f (M ) називають |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Повний диференціал функції |
|
|
dz z dx z dy |
|
||||||||||||||||
|
z f (x, y) |
|
|
|
|
|
|
|
x |
|
|
|
y |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u f (x, y, z) |
du |
u dx |
u dy |
u dz |
|
|||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
y |
|
|
|
|
z |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
u f(x1, x2, ..., xn ) |
|
|
|
|
du u dxi |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
x |
i |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Частинні диференціали функції |
d z z dx, |
|
d z z dy |
|
||||||||||||||||
|
z f (x, y) |
|
x |
|
|
|
x |
|
|
|
|
y |
|
|
|
y |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
u f (x1, x2, ..., xn ) |
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx u |
|
dxk , k 1, n |
|
||||||||||||||||
|
|
|
|
xk |
|
||||||||||||||||
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Диференціал 2-го порядку функції |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z f (x, y) незалежних змінних x, y |
d2z z dx2 |
2z dxdy z dy2 |
|
|||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
|
xx |
|
|
|
|
|
xy |
|
|
|
|
|
|
yy |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Диференціал m -го порядку функції |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
||||
|
z f (x, y) незалежних змінних x, y |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
d |
|
z |
|
|
|
dx |
|
|
|
dy z |
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
y |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 Розділ 1. Диференціальне числення функцій кількох змінних
1.5. Похідна за напрямом. Градієнт
Похідна за напрямом. Похідною |
|
Властивості похідної за |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
функції u f (M ) за напрямом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(M |
0 ) |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
l |
|
|
|
напрямом. Величина |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
у точці M0 називають |
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
визначає швидкість зміни функції в |
|||||||||||||||||||||||||||||||||||||
|
u(M |
|
) |
|
|
|
|
|
|
|
f ( |
|
|
tl 0 ) f ( |
|
|
) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
r |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
точці M0 за напрямом l , а знак |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
lim |
|
0 |
0 |
, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
t 0 |
|
|
|
|
t |
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(M0 ) — характер її зміни |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
де l |
— орт вектора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
l , r0 OM0. |
|
l |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(зростання або спадання). |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Похідна функції за напрямом |
|
|
|
|
|
|
|
|
|
|
u(M0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
u u(x,y), l |
|
|
|
|
|
|
|
|
|
|
u(M |
0) |
|
|
|
|
|
|
|
|
|
|
|
u(M0) |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
cos |
|
sin |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(M0) |
|
|
|
u(M0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
u u(x,y,z), l |
0 |
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(M |
|
) |
|
|
|
|
|
|
|
|
|
|
u(M |
|
|
) |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
cos |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
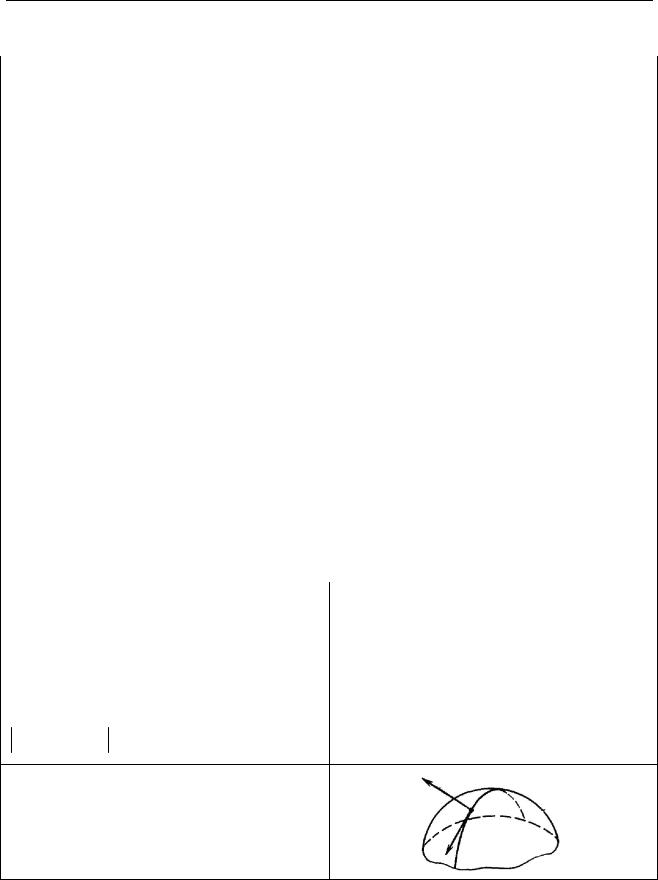
Градієнт. Градієнтом |
|
|
|
|
|
|
|
grad u(M0 ) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
диференційовної функції u f (M ) у |
|
|
u(M0 ) |
|
|
|
u(M0 ) |
|
|
|
|
u(M0 ) |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
точці M0 |
називають вектор |
|
|
|
i |
|
j |
k |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Зв’язок між похідною за напрямом |
|
u |
(grad u, |
|
0 ) pr |
|
0 |
grad u |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
l |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
і градієнтом функції |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Властивості градієнта. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
1. У напрямі grad u(M0 ) |
|
функція |
|
|
|
|
u(M0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
0 |
|
|
max |
|
|
grad u(M0 ) |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
зростає з найбільшою швидкістю |
|
|
|
|
|
l |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
grad u(M0 ) .
2. Градієнт функції u у точці M0 |
grad u(M0 ) |
|
|
u C |
|
напрямлений уздовж нормалі до |
|
M0 |
поверхні рівня u(x, y, z) C, що |
|
|
проходить через точку M0. |
|
L |
|
||
