методичка 2 семестр интегралы

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный технический университет Украины «Киевский политехнический институт»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1) y 2xy xe x2 ;

2) (1 x2 )y 2xy (1 x2 )2;

x cosy a sin 2y

.pdf

Скачиваний:

Добавлен:

12.05.2015

Размер:

5.01 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 1917 18 19 > Следующая >>>

20. Лінійні диференціальні рівняння 1-го порядку. Рівняння Бернуллі

161

Коментар. Це ЛДР щодо невідомої i i(t). Його можна розв’язати за методом Бернуллі або Лаґранжа.

Бачимо, що із плином часу t (t ) сила струму i(t) наближається до сталого значення ER0 .

20.3. Зінтегрувати ДР y 2xy 2x3y3.

Розв’язання. [3.2.8.]

Це рівняння Бернуллі, яке розв’язуємо методом Бернуллі: y u(x)v(x),y u v uv .

2vx 0,

u(v 2vx) vu 2x u v

3 3 3

2x u v .

2xv

0 v e x2 ;

3 3 2x

3 2x2

dx;

2x u e

2x e

x2de 2x2 1 x2e 2x2

1 e 2x2

2 2x2

2x2

x e

C1,

C e2x2 x2 1 .

Розв’язок y 0 можна одержати, коли C . Загальний інтеграл ДР:

	2x	2		2	1		2
	2x		x	2	1		2	1	0.
Ce			x			y		1	0.
					2
					2

Задачі для аудиторної і домашньої роботи

20.4. Зінтегруйте рівняння:

20.5. Розв’яжіть задачу Коші:

1) y y tg x	1	,y(0)	0;	2) y y cos x cos x,y(0) 1;

	cos x

162	Розділ 3. Диференціальні рівняння

3)t(1 t2 )dx (x xt2 t2 )dt, x(1) 4 ;

4)yx x 4y3 3y2,y(2) 1.

20.6.1) Знайдіть лінію, у якої початкова ордината будь-якої дотичної на дві одиниці менше за абсцису точки дотику.

2)Знайдіть силу струму i(t) в електричному колі з опором R і самоіндукці-

єю L, за умови, що E(t) E0 sin 2 nt,i(0) I0, де I0,E0 const.

3)Знайдіть лінію, у якої будь-яка дотична перетинає вісь ординат у точці, однаково віддаленій від точки дотику і від початку координат.

4)Знайдіть лінію, у якої площа трапеції, утвореної осями координат, ординатою довільної точки і дотичною в цій точці, дорівнює половині квадрата абсциси.

5)Знайдіть лінію, для якої площа фігури, обмеженої віссю абсцис, двома ординатами і дугою MM цієї лінії, пропорційна дузі MM .

6)Точка масою m 6 г рухається прямолінійно. На неї діє сила, пропорційна часові (коефіцієнт пропорційності k1 4). Крім того, на точку

діє опір середовища, пропорційний швидкості (коефіцієнт пропорційності k2 2). Знайдіть залежність швидкості від часу, вважаючи, що в по-

чатковий момент швидкість дорівнює нулеві.

20.7. Зінтегруйте рівняння:

1) y 2xy 2x3y3;	2) y y tg x y2 cos x 0;
3) (x3 ey )y 3x2;	4) y	2x	.

		x2 cosy a sin 2y

20.8.Розв’яжіть задачу Коші:

1)y 9x2y (x5 x2 )y23,y(0) 0;

2)xy y y2 ln x,y(1) 1.

Відповіді

	x2		x	2
	x2		x
20.4. 1) y e		C			; 2)	y (x
20.4. 1) y e		C	2		; 2)	y (x
			2

4) x 2a(sin y 1) Cesin y.

20.5. 1) y cosx x ; 2) y 1; 3) x

C )(1 x2 ); 3) x Ce2y	y2	y	1	;
	2	2	4

t arctg t; 4) x y2 y3.

21. Рівняння, що дозволяють пониження порядку

163

20.6. 1) y Cx x ln x 2; 3) x2 y2 Cx; 4) y x Cx2; 5) ланцюгова лінія;

6) m dvdt k1t k2v,v(0) 0,v(t) 2 t 3 3e t3 .

20.7.	1)	1				2x2					2			1			2) y(x C )		1		; 3)	3	y	C y;
			Ce					x							;							x e
		y2	Ce					x						2	;			cos x				x e
		y2												2				cos x
4) x2	Cesin y 2a(sin y												1).
				2		x	3		1			3		2		3				1
20.8.	1)			2		x			1			3		2			,y 0; 2) y			1
		y			e					x												.
		y			e					x												.
									9					9					ln x 1
			9						9					9					ln x 1

21. Рівняння, що дозволяють пониження порядку

Навчальні задачі

21.1. Розв’язати задачу Коші y cos 2x,y(0) 1,y (0) y (0) 0.

Розв’язання. [3.3.1.]

Маємо ДР вигляду y f (x).

[Розв’яжемо ДР безпосереднім інтегруванням, поступово визначаючи значення сталих.]

			y cos 2xdx											1 sin 2x				C1;
			y (0)											2
			y (0)				0 C				1			0 C			1	0.
											1						1
y		1	sin 2x; y					1			sin 2xdx								1		cos 2x C				;
y			sin 2x; y					2			sin 2xdx										cos 2x C				;
	2																	4				2
	2																	4
		y (0)		0					1	C				0		C							1	.
		y (0)		0						C			2	0		C				2				.
							4						2							2		4
							4															4
1	1						1															1				1
y 4 cos 2x	4 ;			y			4 (cos 2x 1)dx															8 sin 2x				4 x C3	;
			y(0) 0 C3									1 C3						1.
Розв’язок задачі Коші y 1 sin 2x												1 x 1.
				8								4
21.2. Знайти загальний розв’язок ДР y															y	x.
21.2. Знайти загальний розв’язок ДР y															x	x.
Розв’язання. [3.3.2.]															x
Розв’язання. [3.3.2.]
Це ДР, яке не містить невідомої функції в явному вигляді F(x,y,y ) 0.
Позначаємо [запроваджуючи нову функцію]

					y	p(x),y
					y	p(x),y								p		(x).
							p p						x.
												x

164	Розділ 3. Диференціальні рівняння

Одержали лінійне ДР 1-го порядку, яке розв’яжемо методом Бернуллі [3.2.8]:

p u(x)v(x), p u v uv ;

v u

uv x.

;

;u(x) x.

x;v 1;v(x) x C

;

dy p(x) x(C

C x x2;

y (C1x x2 )dx

Загальний розв’язок рівняння y

C2.

21.3. Розв’язати задачу Коші: yy

lny,y(0)

(y )

1,y (0)

Розв’язання. [2.19.4.]

Це задача Коші для ДР, яке не містить аргументу функції в явному вигляді

F(y,y ,y ) 0. Позначаємо [запроваджуючи нову функцію]

y p(y); yxx p dpdy .

yp dpdy p2 y2 ln y; dpdy yp y lnp y .

Одержане рівняння Бернуллі розв’яжемо методом Бернуллі:

p uv, p u v uv .

y ln y

v u

y ln y

u 0;du

;u y.

ln y

;vdv

ln ydy

;

ln2 y

p(y) yln2 y C1 .

21. Рівняння, що дозволяють пониження порядку

165

Визначимо сталу C1 з початкової умови: p(y(0)) 1

p(1) 1.

p(1) C1 1

C1 1.

y ln2 y 1;

dx;

ln2 y 1

dln y

x 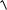ln2 y 1 ln ln y ln2 y 1 C2.

Визначимо сталу C2 з умови y(0) 1.

0 0 C2 C2 0.

Розв’язок задачі Коші x ln ln 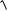y 1 ln2 y .

Задачі для аудиторної і домашньої роботи

21.4. Зінтегруйте рівняння:

1) y

x sin x;

2) y arctg x;

3) yIV

4) y

cos 2x;

5) xy y ;

6) y

7) y

2 ctg x y

sin

8) 2yy

;

3(y )

9) xy y 1 x;

10) y 2

y 2

21.5.Розв’яжіть задачу Коші:

1)y xex ,y(0) y (0) 0;

2)y (x 2)5 1,y( 1) 121 ,y ( 1) 14 ;

3)y (x2 1) 2xy , y(0) 1,y (0) 3;

4)y y x2 , y(2) 0,y (2) 4;

5)2y 3y2,y( 2) 1, y ( 2) 1;

6)y3y 1,y(1) 1,y (1) 0.

166	Розділ 3. Диференціальні рівняння

Відповіді

21.4. 1) y

sin x C x C

;

2) y

arctg x

(x2

ln(1

x2) C x C

;

3) y

C x3

C x2

C x C

;

4) y

sin 2x

C x2

C x C

;

120

sin

5) y C1x

C2;

6) y

C1x

C2; 7) y

sin 2x

;

8) y cos2(x C

) C

; 9)

C x ln

C x C

;

10) y sin(C1 x) C2x C3.

21.5. 1) y (x 2)ex x 2; 2)

;

3) y x3

3x 1;

12(x 2)

2 x2

16 ;

4) y

5) y

; 6) y 2x x2 .

(x 4)2

22. Лінійні однорідні диференціальні рівняння. Метод Ейлера

Навчальні задачі

22.1.1.Знайти фундаментальну систему розв’язків і загальний розв’язок ДР y y 2y 0.

Розв’язання. [3.5.]

Маємо ЛОДР 2-го порядку.

[Складаємо характеристичне рівняння.]

2 2 0.

[Розв’язуємо рівняння і виписуємо відповідні кореням характеристичного рівняння лінійно незалежні розв’язки ЛНДР.]

1 1 y1 ex ,2 2 y2 e 2x .

ФСР диференціального рівняння [3.5.8]: {ex ,e 2x }.

Загальний розв’язок ДР [3.5.9]: y C1ex C2e 2x .

22.1.2.Знайти фундаментальну систему розв’язків і загальний розв’язок ДР y 2y 26y 0.

Маємо ЛОДР 2-го порядку зі сталими коефіцієнтами:

2 2 26 0;

1,2 1 5i y1,2 e x cossin 55xx .

22. Лінійні однорідні диференціальні рівняння. Метод Ейлера

167

ФСР рівняння [3.5.8]: {e x cos 5x,e x sin 5x}.

Загальний розв’язок [3.5.9]: y C1e x cos 5x C2e x sin 5x.

Коментар.Замінюємо y 1,y ,y 2.

22.1.3.Знайти фундаментальну систему розв’язків і загальний розв’язок ДР y 6y 9y 0.

Розв’язання. [3.5.]

Маємо ЛОДР 2-го порядку зі сталими коефіцієнтами:

2 6 9 0;

1,2 3 y1 e3x ,y2 xe3x .

ФСР рівняння [3.5.8]: {e3x , xe3x }.

Загальний розв’язок [3.5.9]: y C1e3x C2xe3x .

22.2. Розв’язати задачу Коші:

y 6y 11y 6y 0,y(0) y (0) 0,y (0) 4.

Розв’язання. [3.5.]

Маємо задачу Коші для ЛОДР 3-го порядку зі сталими коефіцієнтами.

		3 6 2 11 6 0;
1 ex ;						2	2 e2x ;					3	3 e3x .
1						2						3
ФСР рівняння [3.5.8]: {ex ,e2x ,e3x }.
Загальний розв’язок рівняння [3.5.9]:
		y C ex C e2x									C e3x .
[Враховуємо початкові умови.]					1					2	3
[Враховуємо початкові умови.]
		y C ex					2C e2x				3C e3x ;
					1					2		3
		y C1ex 4C2e2x 9C3e3x .
Використовуючи початкові умови, одержуємо систему щодо C1,C2,C3 :
		C		C				0,						2,
C	1	C	2	C			3	0,			C		1	2,
	1		2				3						1

		2C			3C					0,					4,
C	1	2C		2	3C				3	0,	C		2		4,
	1			2					3				2
		4C			9C					4.					2.
C	1	4C		2	9C				3	4.	C		3		2.
	1			2					3				3

Розв’язок задачі Коші y 2ex 4e2x 2e3x .

Задачі для аудиторної і домашньої роботи

22.3. Знайдіть загальний розв’язок рівняння:

1) y y 2y 0;

2) y 9y 0;

168	Розділ 3. Диференціальні рівняння

3) y 4y	0;		4) y 2y y 0;
5) 4 d2x 20 dx		25x 0;	6) y y 0;
dt2	dt
7) y 6y	13y 0;		8) 4y 8y 5y 0;
9) y 9y	0;		10) y(4)	13y 36y 0;
11) y(4) 8y 16y 0;			12) y(4)	16y 0.

22.4.Розв’яжіть задачу Коші:

1)y 4y 3y 0, y(0) 6,y (0) 10;

2)4y 4y y 0, y(0) 2,y (0) 0;

3)y 4y 29y 0, y(0) 0,y (0) 15.

22.5.Складіть ЛОДР, знаючи їхні характеристичні рівняння:

1) 9 2 6 1 0;	2) 2 3 2 0;
3) 2 2 3 5 0;	4) ( 1)( 2) 0;

5)( 2 1)2 0.

22.6.Складіть ЛОДР, якщо відомі корені характеристичних рівнянь, і запишіть їхні загальні розв’язки:

1) 1								1, 2 2;												2) 1 1, 2							1;
3) 1 3 2i, 2 3 2i;																				4) 1 1, 2 1, 3 1.
Відповіді
22.3. 1) y C ex C e 2x ;											2) y C e3x						C e 3x ; 3)						y C e4x		C				;
								1		2						1			2				1					2
4) y ex(C						1	C x);			5) x (C			1	C t)e5t 2;					6) y	C		1	cos x C		2	sin x;
						1		2					1			2						1			2
	3x																	x			x			x
7) y e	3x				(C1 cos 2x					C2 sin 2x);						8) y e		x			x		C2 sin	x
7) y e					(C1 cos 2x					C2 sin 2x);						8) y e			C1 cos				C2 sin		;
																					2
																					2			2
9) y C		1	cos 3x C						2	sin 3x C				3	;	10) y C e2x				C e 2x C e3x								C e 3x ;
		1							2					3					1		2			3					4
11) y (C				1		C x)e2x (C					3	C x)e 2x ;					12) y C e2x						C e 2x	C			3	cos 2x C		4	sin 2x.
				1				2			3				4					1			2				3			4

22.4.1) y 4ex 2e3x ; 2) y e x2(2 x).

22.5.1) 9y 6y y 0; 2) y 3y 2y 0; 3) 2y 3y 5y 0;

4) y 3y 2y 0; 5) y(4) 2y y 0.

23. Лінійні неоднорідні диференціальні рівняння із сталими коефіцієнтами

169

22.6. 1) y 3y 2y 0, y C1ex C2e2x ; 2) y 2y y 0, y (C1x C2)ex ;

3) y 6y 13y 0, y e3x(C1 cos 2x C2 sin 2x);

4)y 3y 3y y 0, y ex (C1 C2x C3x2).

23.Лінійні неоднорідні диференціальні рівняння із сталими коефіцієнтами

Навчальні задачі

23.1. Знайти загальний розв’язок ЛНДР y y	1	.

	cos3 x
Розв’язання. [3.6.1, 3.6.2.]	cos3 x
Розв’язання. [3.6.1, 3.6.2.]

[Оскільки права частина ЛНДР має загальний вигляд, то загальний розв’язок рівняння знайдемо методом Лаґранжа.] [Крок 1. Розв’язуємо відповідне однорідне рівняння.]

	y y 0;
	1,2	y			cos x,
2 1 0;	1,2	i	1		sin x.
		y		2	sin x.
				2

[Крок 2. Записуємо у якому вигляді шукатимемо загальний розв’язок ЛНДР.] y C1(x)cos x C2(x)sin x.

[Крок 3. Функції C1(x),C2(x) знаходимо з алгебричної системи

					(x)y	(x) 0,
C		(x)y		(x) C	(x)y	(x) 0,
	1		1	2	2

C (x)y (x) C (x)y (x) f(x),
	1		1	2	2
	1		1	2	2

яку можна розв’язати за методом Крамера.]

C1 cos x C

2 sin x 0,

cos x

sin x C

C sin x C cosx

;

sin x

cos x C

cos x

cos

cos x

sin x

cosx

sin x

cos x

sin x

;

cos x

sin x

cos3 x

cos2 x

cos3 x

sin x

;

cos3 x

cos2 x

170	Розділ 3. Диференціальні рівняння

[Крок 4. Знаходимо C1(x),C2(x).]

C	(x)				d cos x				1	A ;
C	(x)			cos3 x						A ;
1									2 cos2 x	1
									2 cos2 x
		C2					dx	tg x A2.


Загальний розв’язок ЛНДР					cos2 x
Загальний розв’язок ЛНДР
					1
					1
y A1					2		cosx tg x A2 sin x.
					2
			2 cos			x

23.2. Записати вигляд частинного розв’язку ДР y 5y x2 1 (з невизначеними коефіцієнтами).

Розв’язання. [3.7.]

Маємо ЛНДР 2-го порядку зі спеціальною правою частиною.

[Розв’язуємо характеристичне рівняння для однорідного рівняння. ]

3 5 2 0;1,2 0, 3 5.

[Аналізуємо праву частину диференціального рівняння.]

Функція f (x) x2 1 є правою частиною спеціального вигляду — «многочлен 2-го порядку»; йому відповідає число k 0 [3.7.1].

[Перевіряємо чи відбувається збіг власних чисел правої частини з розв’язками характеристичного рівняння.]

Є «резонанс» 2-го порядку, оскільки 1 2 k.

[Записуємо шаблон для частинного розв’язку ЛНДР.]

yчаст. неодн. x2(Ax2 Bx C ).

23.3.1. Знайти загальний розв’язок ДР y 5y 6y 6x2 2x 5.

Розв’язання. [3.6.3, 3.7.]

Маємо ЛНДР 3-го порядку зі сталими коефіцієнтами.

[Крок 1. Записуємо теорему про структуру розв’язку ЛНДР.]

yзаг. неод. yзаг. одн. yчаст. неодн.

[Крок 2. Знаходимо загальний розв’язок відповідного ЛОДР методом Ейлера).] y 5y 6y 0;

3 5 2 6 0;

1 0 y1 1; 2 2 y2 e2x ; 3 3 y3 e3x .

ФСР рівняння: {1,e2x ,e3x }.

yзаг. одн. C1 C2e2x C3e3x .

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 1917 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.20194.29 Mб92Методическое пособие для барменов.doc
#
09.11.2019540.16 Кб2Методическое____пособие_инструктору_АФФ.doc
#
11.11.2019304.13 Кб9методичка 5 курс (правильная).doc
#
17.03.20161.6 Mб139Методичка (дискретка).pdf
#
05.11.2018265.73 Кб5методичка 2 курс спецфакультет (1).doc
#
12.05.20155.01 Mб42методичка 2 семестр интегралы.pdf
#
12.11.2019111.71 Кб2Методичка 4 курс МП ММІ .doc
#
12.05.2015265.22 Кб37МЕТОДИЧКА 5 КУРС.doc
#
09.11.2019181.25 Кб0Методичка 5курс (1 часть).doc
#
09.11.2019143.36 Кб2Методичка 5курс (2 часть).doc
#
20.12.2018287.74 Кб1Методичка VC++6укр.doc