Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный технический университет Украины «Киевский политехнический институт»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

методичка 2 семестр интегралы

.pdf

Скачиваний:

Добавлен:

12.05.2015

Размер:

5.01 Mб

Скачать

☆

<<< < Предыдущая 12 / 192 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Розділ 1. Диференціальне числення функцій кількох змінних

1.6. Вектор-функція дійсного аргументу

Вектор-функція дійсного

аргументу. Якщо кожному значення

a ax (t)i

ay(t)j az (t)k

дійсної змінної t D поставлено

ax (t)

у відповідність вектор a(t) , то

(t)

кажуть, що на множині D задано

, t D

вектор-функцію a a(t) дійсної

(t)

змінної t.

Годограф. Годографом вектор-

x(t),

функції r r (t) називають лінію, яку

y(t),

описує у просторі кінець вектора

a(t)

z(t)

a1(t)

Будь-яку лінію у просторі можна

розглядати як годограф деякої вектор-

a2(t)

функції.

Границя вектор-функції

0 ( ) 0 t :

lim

(t) A

t t0

(t) A

t t0

Неперервність вектор функції.

Вектор-функція

(t) неперервна в

lim

(t)

(t0 )

точці t0, якщо

t t0

Похідна вектор-функції

da(t

)

(t t)

)

lim

t 0

dax (t0 )

day(t0 )

daz(t0 )

Дотичний вектор. Якщо

(t),

dr (M0 )

то

є вектором, напрямленим за

r (t0 )

дотичної до годографа вектор-функції

(t) у бік зростання аргументу t.

(t0 t)

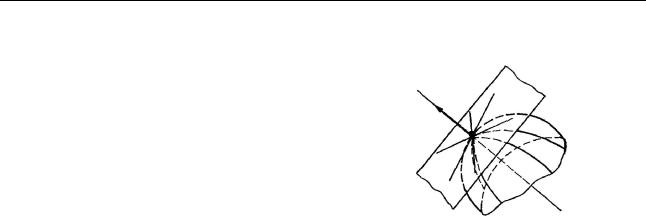
12 Розділ 1. Диференціальне числення функцій кількох змінних

1.7. Дотична і нормаль

Дотична площина і нормаль до

grad u(M0 )

поверхні. Дотичною площиною до

поверхні S у точці M0

називають

площину P, у якій розташовані

дотичні до всіляких кривих, які

проведені на S через M0.

Нормаллю називають пряму L, що проходить через M0

перпендикулярно до P.

Вектор нормалі до поверхні

F(x, y, z) 0

grad F

z f (x, y)

Рівняння дотичної площини до

F (M

)(x x

)

поверхні F(x, y, z) 0 у точці

)(y y

)

M0(x0;y0; z0 )

)(z z

) 0

Рівняння нормалі до поверхні

x x0

y y0

z z0

F(x, y, z) 0 у точці M0(x0;y0; z0 )

Fx (M0 )

Fy(M0 )

Fz (M0 )

Рівняння дотичної площини до

z (M

)(x x

) z (M

)(y y

)

поверхні z f (x, y) у точці

(z z0 ) 0,

M0(x0;y0; z0 )

z0 f (x0, y0 )

Рівняння нормалі до поверхні

x x0

y y0

z z0

z f (x, y) у точці M0(x0;y0; z0 )

zx (M0 )

zy(M0 )

Рівняння дотичної до кривої

x x0

y y0

z z0

)

y (t

)

x x(t),

x(t

), y

y(t

), z

z(t

)

; z

)

L : y y(t), у точці

z z(t)

Рівняння нормальної площини до

x (t0 )(x x0 ) y (t0 )(y y0 )

кривої L у точці M0(x0;y0; z0 )

z (t

)(z z

) 0

Розділ 1. Диференціальне числення функцій кількох змінних

1.8. Локальні екстремуми функції двох змінних

Тейлорова формула. Якщо функція z f (M) диференційовна (m 1) разів

удеякому околі U(M0 ) точки M0(x0;y0), то для будь-якої точки M U(M0 )

правдива Тейлорова формула з центром у точці M0.

df (M

)

dm f (M

)

dm 1f (M

)

f (M ) f (M

)

...

, M

U(M

)

1 !

m !

1)!

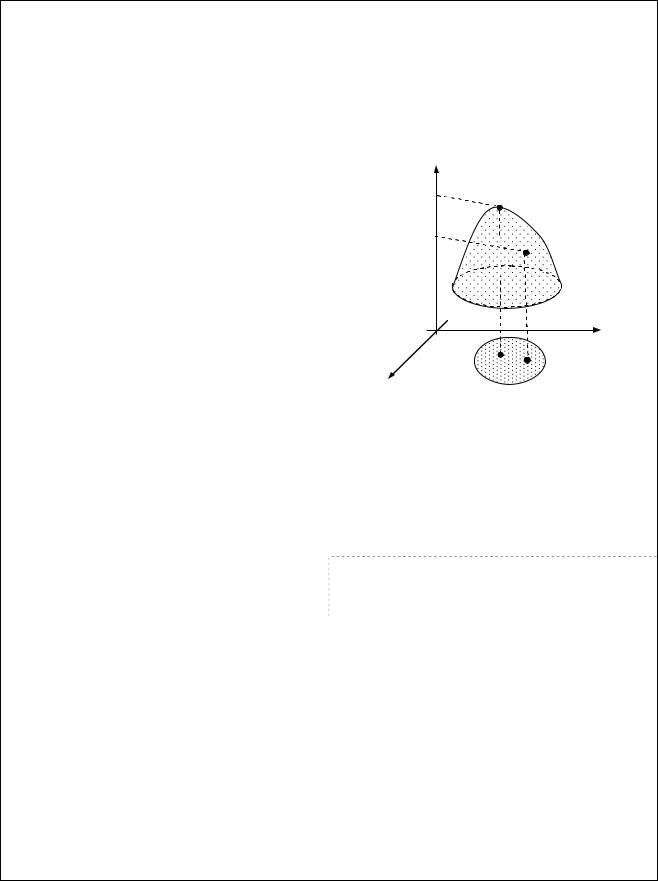
Локальний максимум (мінімум).

Функція z f (x, y) має локальний

z(M0 )

max

максимум (мінімум) у точці M0, якщо

z(M

)

існує такий окіл U(M0 ) точки M0, для

всіх точок якого, відмінних від точки

M0, виконано нерівність

f(M0 ) f(M) (f(M0) f(M)).

Точки локального максимуму та

U(M0 )

мінімуму називають точками

локального екстремуму.

Необхідна умова існування

z(M

)

локального екстремуму. Якщо

dz(M0 ) 0

функція z f (x, y) диференційовна в

z(M

)

точці M0 і має екстремум у цій точці,

то

Точку M0, в якій dz(M0 ) 0,

називають стаціонарною.

Матриця Гессе функції z

f (x, y)

Гессіан функції z f (x, y)

zxx

zxy

det H(x, y)

zxx

zxy

H(x, y)

Позначення

A |

2z(M0 )

, B |

2z(M0 )

,C |

2z(M0 )

x y

det H(M

)

A B

AC B2

B C

14	Розділ 1. Диференціальне числення функцій кількох змінних

Достатні умови локального				1) якщо 0,	то в точці M0	функція
екстремуму. Нехай функція				f має екстремум:
z f (x, y) двічі диференційовна в				f має екстремум:
z f (x, y) двічі диференційовна в				а) коли A 0, мінімум;
точці M0	та деякому її околі і точка			а) коли A 0, мінімум;
точці M0	та деякому її околі і точка			б) коли A 0, максимум;
M0 — стаціонарна точка функції f .				б) коли A 0, максимум;
M0 — стаціонарна точка функції f .
				2) якщо 0,	то в точці M0	функція
				f не має екстремуму;
				3) якщо 0,	то функція потребує
				додаткового дослідження.

 Алгоритм дослідження функції
на локальний екстремум.
1. Визначають область означення				3. Для кожної точки Mi перевіряють
функції.				3. Для кожної точки Mi перевіряють
			0,	достатні умови існування екстремуму і

	z	x		висновують.
		x		висновують.
2. Розв’язуючи систему		0
	z	0

		y
		y

знаходять стаціонарні точки функції f :

M1(x1;y1),..., Mn(xn;yn ).

1.9. Глобальний і умовний екстремум функції двох змінних

Глобальні екстремуми. Якщо		Умовні екстремуми. Функція
функція z f (x, y) диференційовна в		z f (x, y) має умовний максимум
обмеженій замкненій області		(умовний мінімум) в точці M0, якщо
	D D , то вона досягає свого
D	D D , то вона досягає свого	існує такий окіл U(M0 ) точки M0, для
найбільшого (найменшого) значення		існує такий окіл U(M0 ) точки M0, для
найбільшого (найменшого) значення		всіх точок якого, відмінних від точки
або в стаціонарній точці всередині		всіх точок якого, відмінних від точки
або в стаціонарній точці всередині		M0, які справджують умову зв’язку
області D або на межі області D.		M0, які справджують умову зв’язку
		(M ) 0, виконано нерівність
		f(M0 ) f(M) (f(M0) f(M)).

Функція Лаґранжа для
знаходження умовного екстремуму		L(x, y; ) f (x, y) (x, y)
функції f (x, y) з умовою зв’язку
(x, y) 0

Розділ 1. Диференціальне числення функцій кількох змінних				15

Необхідні умови умовного			0,
Необхідні умови умовного	L		0,
екстремуму		x
екстремуму			0,
	L		0,
		y
		(x, y) 0
		(x, y) 0

Достатні умови умовного екстремуму. Нехай функції f (x, y) та (x, y) двічі неперервно диференційовні в околі стаціонарної точки (x0 ;y0; 0 ) функції Лаґранжа

L(x, y; ) f (x, y) (x, y),

тоді, якщо

	2

d L(x0, y0 ; 0 ) 0,
	(x0, y0 ) 0;
	(x0, y0 ) 0;


	2

d L(x0, y0; 0 ) 0,

	(x	, y		) 0;
	(x	, y	0	) 0;
	0		0

то в точці M0(x0 ;y0 ) функція

z f (x, y) має локальний умовний максимум (умовний мінімум).

Алгоритм дослідження функції

2. Усередині кожної ділянки межі

z f(x,y) на глобальний екстремум

i(x,y) 0 знаходять

у замкненій області

стаціонарні точки функції однієї

D L1

... Ln,

змінної

Li : i (x,y) 0,i 1,n.

f(x,y)

i (x,y) 0

1. Розв’язуючи систему

і долучають до розгляду межові точки

цієї ділянки.

3. Обчислюють значення функції у

знайдених точках і вибирають серед

знаходять стаціонарні точки функції

них найбільше та найменше значення

f, які належать області D.

функції в області D.

Алгоритм дослідження функції

2. Знаходять стаціонарні точки функції

на умовний екстремум.

Лаґранжа із системи

1. Записують функцію Лаґранжа.			0,
	L		0,
		x

L(x, y; ) f (x, y) (x, y).			0,
L(x, y; ) f (x, y) (x, y).	L		0,
		y
		(x, y) 0.
		(x, y) 0.

3. У кожній знайденій точці перевіряють достатні умови існування умовного екстремуму і висновують.

Розділ 2. ВИЗНАЧЕНІ ІНТЕГРАЛИ

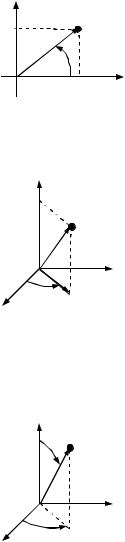
2.1. Недекартові системи координат

Полярні координати

x cos ,

0, ( ; ]

y sin ,

x2 y2 2

x P



Узагальнені полярні координати

x a cos ,

0, ( ; ]

y b sin

Циліндричні координати

x cos ,

0, ( ; ]

y sin ,

z z



Узагальнені циліндричні

x a cos ,

координати

y b sin ,

0, ( ; ]

z z



Сферичні координати

x r cos sin ,

r 0, ( ; ], [0; ]

y r sin sin ,

z r cos

x2 y2 z2 r2



Узагальнені сферичні координати

x ar cos sin ,

r 0, ( ; ], [0; ]

y br sin sin

z cr cos

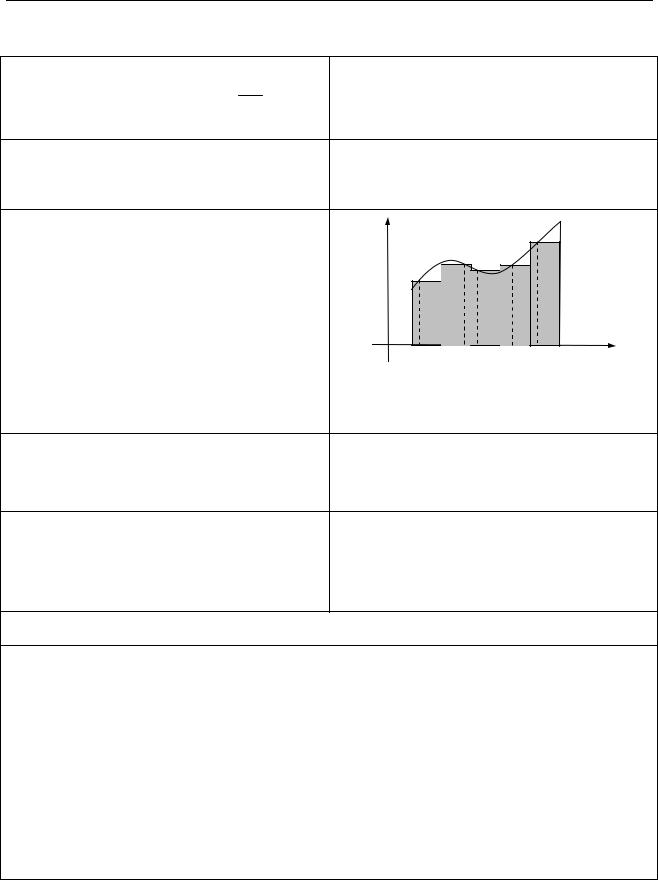
		Розділ 2. Визначені інтеграли						17
2.2. Визначений інтеграл
Розбиття відрізка [a;b]					{x0, x1, ..., xn } :
xi xi	xi 1, i 1, n		a x0	x1		... xn 1 xn		b
xi xi	xi 1, i 1, n
Інтегральна сума для функції				n
f (x), x [a;b]			f ( i ) xi , i				[xi 1;xi ]
			i 1
Визначений	інтеграл від функції		y				B
f (x) у межах від x a до x b :						y f(x)
b		n		A
f(x)dx	lim	f ( i ) xi .		A
f(x)dx	lim	f ( i ) xi .
max xi		0 i 1					n
a	(n )						n
					1	i
Функцію f (x) називають інтегровною			O	a	x1 xi 1 xi		xn 1 b	x
на відрізку [a;b], якщо границя
скінченна.
Геометричний зміст визначеного						b
інтеграла. Площа криволінійної						f (x)dx	S
трапеції aABb, якщо f (x) 0						a
Достатня умова інтегровності.			Кусково-неперервна обмежена
Якщо функція кусково-неперервна і			функція має скінченну кількість точок
обмежена на відрізку [a;b], то вона			розриву 1-го роду або не має їх
інтегровна на цьому відрізку.			узагалі.
Властивості визначеного інтеграла.

	b	b
1)		f(x)dx f (t)dt	(незалежність від змінної інтегрування);
	a	a

	b		b	b
2)	( f(x) g(x))dx f(x)dx g(x)dx (лінійність);
	a		a	a

	b	c	b
3)		f (x)dx f (x)dx	f (x)dx	(адитивність);

Розділ 2. Визначені інтеграли

4) f (x)dx f(x)dx (орієнтованість), f (x)dx 0;

5) m(b a)

f(x)dx M(b a), де m min f (x), M max f (x);

x [a;b]

6) якщо f (x) 0, x [a;b],a b, то f (x)dx 0 (збереження знаку);

7) якщо f (x) g(x), x [a;b],a b, то f (x)dx

g(x)dx (монотонність);

8) якщо функція f інтегровна на [a;b]

(a b), то

f (x)dx

f (x)

dx.

Теорема про середнє значення

функції. Якщо функція f неперервна

f(x)dx f (c)(b a)

на відрізку [a;b], то знайдеться така

точка c (a;b), що

2.3. Обчислення визначеного інтеграла

Теорема Бароу. Якщо функція f (t)

Формула Бароу:

неперервна на відрізку [a;b], то

f(t)dt f (x),a x b

функція F(x)

f (t)dt є первісною

для функції f (x).

Теорема Ньютона — Лейбніца.

формула Ньютона — Лейбніца:

Якщо функція f (x) неперервна на

ab F(b) F(a),

відрізку [a;b] і функція F(x) є

f (x)dx F(x)

первісною для функції f (x) на [a;b],

F (x) f (x)

то правдива

Розділ 2. Визначені інтеграли

Інтегрування частинами у

формула інтегрування частинами у

визначеному інтегралі. Якщо функції

визначеному інтегралі:

u(x) та v(x) неперервно

диференційовні на відрізку [a;b],

udv uv

vdu

то правдива

Заміна змінних у визначеному

формула заміни змінної

інтегралі. Якщо функція f (x)

у визначеному інтегралі

неперервна на [a;b] і x (t) —

неперервно диференційовна функція

на [ ; ], де a ( ),b ( ),

f (x)dx f( (t)) (t)dt

причому f ( (t)) означена і неперервна

на [ ; ], то правдива

Інтеграл від парної функції f за

симетричним відрізком

f (x)dx

2 f (x)dx

Інтеграл від непарної функції f

за

симетричним відрізком

f (x)dx

Інтеграл від T -періодичної функції

a T

f(x)dx f (x)dx

Формула Валіса

n 2k 1,

(n 1)!!

(sin x)

(cos x) dx

n !!

2k, k

Тригонометричні підстанови

R x,

x a sin t, t

;

x a tg t, t

;

, t

cos t

20 Розділ 2. Визначені інтеграли

2.4. Застосування визначеного інтеграла

Площа криволінійної трапеції:

S f (x)dx

y f (x) 0, x a, x b, y 0

Площа фігури, обмеженої лініями

f(x) g(x)

y f (x), y g(x), x a, x b

Площа криволінійного сектора

( ), ,

2( )d

в полярних координатах

Площа криволінійної трапеції,

обмеженої кривою, заданою

y(t)x (t)dt

x(t),

[t ;t

]

y(t),

параметрично: y

Об’єм тіла за відомими площами

перерізів S(x), перпендикулярних до

V S(x)dx

осі Ox

Об’єм тіла, одержаного

обертанням криволінійної трапеції

V f 2(x)dx

навколо осі Ox

Об’єм тіла, одержаного

обертанням криволінійної трапеції

V 2 xf (x)dx

навколо осі Oy

Довжина дуги кривої

y f (x), x [a;b]

1 (f (x)) dx

Площа поверхні обертання,

утвореної обертанням кривої

Q 2 f (x) 1 (f (x))2dx

y f (x), x [a;b],

навколо осі Ox

Шлях, пройдений матеріальною

точкою із швидкістю v v(t) за

s v(t)dt

проміжок часу [t ;t

]

<<< < Предыдущая 12 / 192 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.20194.29 Mб92Методическое пособие для барменов.doc
#
09.11.2019540.16 Кб2Методическое____пособие_инструктору_АФФ.doc
#
11.11.2019304.13 Кб9методичка 5 курс (правильная).doc
#
17.03.20161.6 Mб139Методичка (дискретка).pdf
#
05.11.2018265.73 Кб5методичка 2 курс спецфакультет (1).doc
#
12.05.20155.01 Mб42методичка 2 семестр интегралы.pdf
#
12.11.2019111.71 Кб2Методичка 4 курс МП ММІ .doc
#
12.05.2015265.22 Кб37МЕТОДИЧКА 5 КУРС.doc
#
09.11.2019181.25 Кб0Методичка 5курс (1 часть).doc
#
09.11.2019143.36 Кб2Методичка 5курс (2 часть).doc
#
20.12.2018287.74 Кб1Методичка VC++6укр.doc