методичка 2 семестр интегралы

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный технический университет Украины «Киевский политехнический институт»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

divadxdydz

.pdf

Скачиваний:

Добавлен:

12.05.2015

Размер:

5.01 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 1915 16 17 18 19 > Следующая >>>

16. Поверхневий інтеграл 2-го роду

141

16.1.3. Обчислити z2dxdy,			де — зовнішній


y R2 x2 z2 .

Розв’язання. [2.18.5.]

Оскільки поверхня проектується на площину Oxy неодно-

значно, то розіб’ємо поверхню на частини 1 та 2, роз-

ташовані відповідно вище й нижче площини z 0.



z2dxdy z2dxdy z2dxdy.

бік півсфери

z 1 n1

2 y x n2

Рис. до зад. 16.1.3

Поверхні 1 та 2 проектуються на площину Oxy в одну й ту саму область

DOxy . Зовнішня нормаль до 1 утворює з віссю Oz гострий кут, а до 2 — тупий. Отже,

	[2.18.5]
z2dxdy	(R2			x2	y2)dxdy;
1	DOxy
	[2.18.5]
z2dxdy	(R2			x2	y2)dxdy;
2	DOxy
	z2dxdy 0.

Коментар. Властивість адитивності поверхневого інтеграла.
16.2. Знайти потік векторного поля
			xi	yj	zk через зовнішній бік ча-
		a	xi	yj	zk через зовнішній бік ча-
стини поверхні : x2	y2 a2		(0 z a).

Розв’язання. [2.20.8.]

Потік векторного поля знаходять за формулою

[2.20.8]

(a ) (a,n 0)d .

Проектуємо поверхню на площину Oxz. Оскільки вона проектується неоднозначно, то розіб’ємо її на частини

1 {y 0} та 2

{y 0}.

[2.18.6]

0 )d

(a,n0 )

dxdz.

cos

DOxz

y y(x,z)

2		z	1
		z

				n10

	20
n	20

x z a

		x
O	a	x

Рис. до зад. 16.2

На 1 маємо:

142	Розділ 2. Визначені інтеграли

a2 x2 .

F(x,y,z) x2 y2 a2 0.

.

grad F 2xi

2yj

2xi

2yj

;

4x2

4y2

, cos

x2 y2

(a,n

) (x;y,z)

;

x2 y2 .

x2 y2

(

0 )

cos

a2 x2

y a2 x2

a2dxdz

(

) (

0 )dS

a2 dz

a2 x2

Oxz

a2 a arcsin ax a a3.



2 a3;

1 2 2 a3.

Коментар. Для 1 нормаль утворює гострий кут з віссю Oy.

Потік для 2 обчислюють так само.

Задачі для аудиторної і домашньої роботи

16.3. Обчисліть:

1)	x2dydz y2dxdz z2dxdy,	де	— зовнішній бік поверхні півс-

фери x2 y2 z2 R2 (z 0).
2)	xdydz ydzdx zdxdy,	де	— внутрішній бік сфери

x2 y2 z2 R2.

							17. Теорія поля	143
			2	y	2
	x			y
3)							де —	внутрішній бік поверхні

		16		9		dxdy,
		16		9

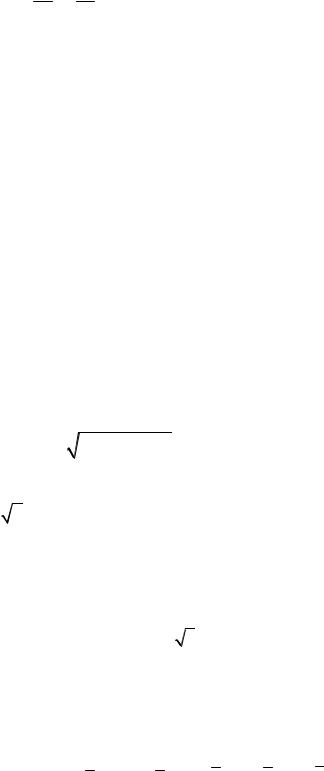
z 4 x2 y2 , відтятої площиною z 0.

16 9

	4) ydxdz,												де — верхній бік частини площини x y z a, що

	лежить у 1-му октанті.
16.4.	Знайти потік поля																	через орієнтовану поверхню :
16.4.	Знайти потік поля																a	через орієнтовану поверхню :
	1)							(x 2z;x 3y z;5x y), — протилежний початку коорди-
	1)		a					(x 2z;x 3y z;5x y), — протилежний початку коорди-
	нат бік трикутника з вершинами (1;0;0),																										(0;1;0),(0;0;1);
	2)										(y2 ;x 2 ;z2 ),										—					частина	зовнішнього	боку	циліндра
	2)							a			(y2 ;x 2 ;z2 ),										—					частина	зовнішнього	боку	циліндра
	x2 y2											a2, розташованого в 1-му октанті між площинами																	z 0 і
	z a,a 0;
	3)									(3x; y; z),											—					частина зовнішнього боку параболоїда
	3)					a				(3x; y; z),											—					частина зовнішнього боку параболоїда
	x2 y2											9 z, розташованої в 1-му октанті;
	4)										(xy;yz;zx),											—				частина	зовнішнього	боку	сфери
	4)								a		(xy;yz;zx),											—				частина	зовнішнього	боку	сфери
	x2 y2											z2	1,			розташовану в 1-му октанті;
							x;y;															,
	5)													x2 y2						1						— частина зовнішнього боку поверхні
	5)			a										x2 y2						1						— частина зовнішнього боку поверхні
	гіперболоїда												x2 y2 z2										1, що міститься між площинами						z 0 і
	z
	z									3.
Відповіді
16.3. 1)	R4				; 2) 4 R3; 3) 96 ;															4)	a3
																								.
		2																			6			.
		2																			6
16.4. 1)	5	; 2)						2a4				81			; 4)		3			5) 2
	5							2a4				81					3		;						3 .
	3					3						; 3)	8			16			;						3 .
	3					3							8			16

17. Теорія поля

Навчальні задачі

17.1. Обчислити diva, якщо a x2i y2 j z2k .

Розв’язання. [2.20.3.]

Дивергенцію знаходять за формулою

144	Розділ 2. Визначені інтеграли

[2.20.3]

diva

P(x,y,z) x2,Q(x,y,z) y2,R(x,y,z) z2;

[2.20.3]

(x2)

(y2)

(z2) 2x 2y 2z.

diva

17.2. Знайти потік векторного поля

через зовнішній бік

2xi

2yj

замкненої поверхні : z

(0 z H ).

Розв’язання. [2.20.8, 2.20.10.]

Потік знаходять за формулою

[2.20.8]

(a	)		,		0)d .
		(a		n

Поверхня замкнена, де — поверхня конуса та — частина площини z H, що вирізається конусом. Виконано умови теореми Остроградського — Ґауса [2.20.10].

z


			0
		n	0

	O		y

Рис. до зад. 17.2

div

(2y)

( z) 3

3dxdydz

3 dxdydz

[2.9.3]

3 1

H 2 H H 3.

3Vкон.

Коментар. Об’єм конуса обчислюють за формулою

1 S

кон.

осн.

17.3.Знайти потік векторного поля a 2xi 2yk zk через внутрішній бік частини поверхні : z x2 y2 0 z H .

Розв’язання. [2.20.8, 2.20.10.]

Потік знаходять за формулою

[2.20.8]
(a	)	(a	,		0)d .
(a	)	(a	,	n	0)d .

Замкнімо поверхню поверхнею :
							.
;							.

						.

n 0

O y

Рис. до зад. 17.3

17. Теорія поля

145

[Деталі див. у зад. 17.2.]

[2.20.10]

(

)

(

0)d

divadxdydz



3 dxdydz H 3.

diva

[2.20.8]

k ,

)

0)d

(a,n0) z

H dxdy HSкр. H 3.

DOxy

H 3 H 3 2 H 3.

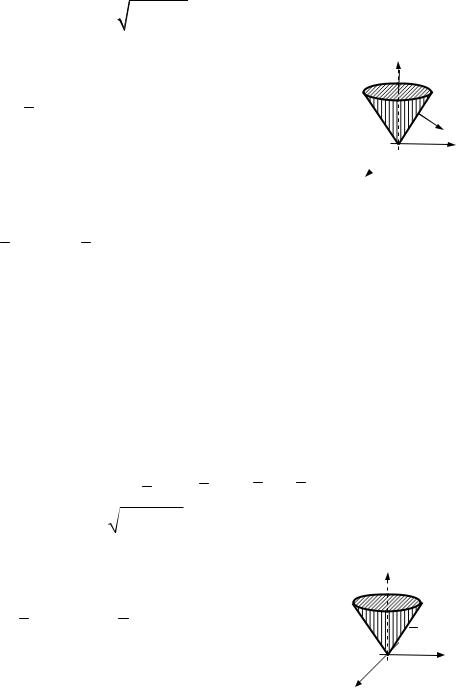
Коментар.  Задача відрізняється від задачі 17.2 тим, що дана поверхня незамкнена, на що вказує слово «частина» та нестрога нерівність в умові задачі. Один із способів обчислення потоку в цьому разі, полягає в замиканні поверхні й обчисленні потоку через замкнену поверхню за допомогою формули Остроградського — Ґауса.

Знак « » у формулі Остроградського — Ґауса вказує на внутрішній бік замкненої поверхні.

Частина поверхні проектується у круг x2 y2 H 2.

17.4.1. Знайти ротор векторного поля

, якщо

zk .

Розв’язання. [2.20.6.]

Ротор знаходять за формулою

[2.20.6]

Qj Rk .

rota



rot

(z)

(y)

(z)

(x)

(y)

(x)

(0 0)

(0 0) k

Коментар. Визначник розкладають за 1-м рядком. Добуток оператора частинного диференціювання на функцію означає взяття відповідної похідної.

146	Розділ 2. Визначені інтеграли

17.4.2. Знайти ротор векторного поля a (xy;2x 3y z;x2 z2)T і найбіль-

шу густину циркуляції цього поля у точці M0(1;2; 1).

Розв’язання. [2.20.6.]

[2.20.6]

rot

xy 2x 3y z

x2 z2

i (0 1) j (2x 0) k (2 x) i 2xj (2 x)k .

Найбільша густина циркуляції — це довжина ротора. max j(M0) rota(M0) .

rot

(M0 )

2xj

(2 x)k

M0(1;2; 1) i 2j

k ;

max j(M)

( 1)2 ( 2)2 12

17.5. Знайти циркуляцію векторного поля

x2y3

вздовж контуру

L : {x2 y2 R2,z z0 } (орієнтованого проти годинникової стрілки якщо дивитися з додатного напряму осі Oz) за Стоксовою теоремою.

Розв’язання. [2.20.9, 2.20.11.]

Циркуляцію векторного поля знаходять за формулою

CL(a ) (a, 0 )dl.

Виконано всі умови теореми Стокса. За формулою Стокса

		[2.20.11]
	,dr)			,		0)d .
(a			(rota		n
L

k L

O x

Рис. до зад. 17.5

За поверхню, напнуту на контур, вибираємо частину площини z z0, обмеженої контуром L. За вектор нормалі — вектор n k (0;0;1)T (оскільки це забезпечує потрібний обхід контуру.

[2.20.6]

0 k

( 3x2y2) 3x2y2k .

rota

x2y3

(rota,n 0) (0;0; 3x2y2) (0; 0;1)T 3x2y2.

									17. Теорія поля																147
											[2.18.5]										[2.7.4]
	C 3 x2y2dxdy											3 x2y2dxdy
																DOxy
			3 5 cos2 sin2													d d
2															2					2
2						R									2					2				[2.3.8]
													R6
	2		2					5									2					4
3 cos		sin		d				d						2			cos				cos		d
0						0								2						0
0						0									0					0
					6					1				1	3			R	6
		2R			6					1				1	3			R		.
		2R																		.
										2		2		2				8
							2			2		2		2	4			8
17.6.1. Перевірити		потенціальність													і		знайти				потенціал				поля

a x2i y2 j z2k .

Розв’язання. [2.21.1, 2.212.]

[Перевіряємо умову потенціальності поля rota 0. ]

[2.20.6]

i (0 0) j (0 0) k (0 0) 0.

rota

Поле a потенціальне.

[Записуємо формулу для потенціалу векторного поля a і знаходимо його.]

[2.21.2]

U(x,y,z)

P(t,y0,z0)dt Q(x,t,z0)dt R(x,y,t)dt C.

U(x,y,z) t2dt t2dt t2dt C

gradU.

соленоїдальним?

17.6.2. Чи є поле a

2xyi

y2zj

(z2y

2yz)k

Розв’язання. [2.21.3.]

[Перевіряємо умову соленоїдальності поля diva 0.]

[2.18.3]

div

(2xy)

( y2z)

(z2y 2yz)

2y 2yz 2zy 2y 0.

[2.20.3]

div

(2xy)

( y2z)

(z2y 2yz) 2y 2yz 2zy 2y 0.

Поле a — соленоїдальне.

148	Розділ 2. Визначені інтеграли

17.6.3. Показати, що векторне поле a (y z)i (x z)j (x y)k гармо-

нічне.

Розв’язання. [2.21.4.]

[Перевіряємо умову гармонічності векторного поля rota 0, div a 0.]

[2.20.3]

diva

(y z)

(x z)

(x y) 0.

[2.20.6]

rot

(1 1)

(1 1)k

y z

x z

x y

Векторне поле

гармонічне.

Задачі для аудиторної і домашньої роботи

17.7. Обчисліть:

1) div

, де

yj zk ; 2) div

;

3) div grad(x2 y2 z2 ).

17.8. Знайдіть:

rota

(M0 ),

j k , M0(1;2; 2);

rot y2

;

z2k

zk .

rot

r , де r

17.9. Перевірте потенціальність і знайдіть потенціал поля:

1) a (y z)i (z x)j (x y)k ;

yzi

2) a

zxj

xyk

;

1 x2y2z2

1 k

ezk ;

17. Теорія поля

149

17.10. З’ясуйте, чи є поле a(M) соленоїдальним, якщо: 1) a x(z2 y2 )i y(x 2 z2 )j z(y2 x2 )k ;

2)a (1 2xy)i y2zj (z2y 2yz 1)k ;

3)a x2yzi xy2zj xyz2k ;


4)		yi	xj	xyk	;

	a
		x2 y2

5) a ln(x2 y2 )i 2 arctg xy j 3k .

17.11. З’ясуйте, чи є поле a(M) гармонічним, якщо:

1) a 6x2i 3 cos(3x 2z)j cos(3y 2z)k ;

2)a (yz 2x)i (xz 2y)j xyk ;

3)a (3x2 3y2 )i (2 6xy)j ;

4)a (2x cos y 2y)i (x2 2 sin y)j .

17.12. Знайдіть потік поля a через поверхню , якщо:

1) a (x 2 ;y2 ;z2 ), — зовнішній бік повної поверхні піраміди, обмеженої площинами x y z 1, x 0, y 0,z 0;

2)a y2zi yz2 j x(y2 z2 )k , — повна зовнішня поверхня цилі-

ндра y2 z2 a2, 0 x a;

3)a (0;y2 ;z), — обмежена частина внутрішнього боку параболоїда z x2 y2, відтятої площиною z 2;

2xi

yj zk , — частина внутрішнього боку параболоїда

y2 z2 Rx, яку відтинає площина x R;

—

повна зовнішня

поверхня

конуса

2xi

2yj

zk ,

x2 y2 z H;

x2yi

xy2

xyzk

— зовнішній бік

повної

поверхні

x2 y2 z2 R2, x 0,y 0,z 0;

150	Розділ 2. Визначені інтеграли

(x;y;z),

—

зовнішній бік

повної

поверхні

z 4 x2, 2x y 4, x 0, y 0, z 0;

(x z3y;xz;z xy),

— зовнішній бік

повної

поверхні

x 0, x 1, y 0, y 2, z 0, z

17.13.Обчисліть за Стоксовою теоремою циркуляцію векторного поля a вздовж контуру L, орієнтованого за годинниковою стрілкою, якщо ди-

витись із початку координат:

y2k

,L : {x2 y2

1,x y z 1};

(y z)

(z x)

(x y)k

L : {4(x2 y2) z2,x y z 1};

,L : {z x2

y2,z y 2};

z3k

,L : {x2 y2 z2

4,x2 y2 z2,z 0};

,L : {y2 z2

9, 3z 4x 5};

x2k

zxi

yzk

,L : {y2 z2

1,x y z 1}.

xyj

Відповіді

17.7. 1)

;

2) 4

;

3) 6.

17.8. 1)

5 k

; 2)

; 3)

2(x y)k

17.9. 1) xy yz zx C;

2) arctg(xyz) C; 3) xy ez

C ; 4) ln(xyz) C.

17.10. 1) ні; 2) так; 3) ні; 4) так; 5) так.

17.11. 1) ні; 2) так; 3) так; 4) ні.

17.12. 1)

;

; 3) 2 ; 4) R3; 5)

H 3; 6)

;

7) 40; 8) 14.

17.13. 1)

;

2) 0; 3) 0;

4) 4 ; 5) 0; 6)

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 1915 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.20194.29 Mб92Методическое пособие для барменов.doc
#
09.11.2019540.16 Кб2Методическое____пособие_инструктору_АФФ.doc
#
11.11.2019304.13 Кб9методичка 5 курс (правильная).doc
#
17.03.20161.6 Mб139Методичка (дискретка).pdf
#
05.11.2018265.73 Кб5методичка 2 курс спецфакультет (1).doc
#
12.05.20155.01 Mб42методичка 2 семестр интегралы.pdf
#
12.11.2019111.71 Кб2Методичка 4 курс МП ММІ .doc
#
12.05.2015265.22 Кб37МЕТОДИЧКА 5 КУРС.doc
#
09.11.2019181.25 Кб0Методичка 5курс (1 часть).doc
#
09.11.2019143.36 Кб2Методичка 5курс (2 часть).doc
#
20.12.2018287.74 Кб1Методичка VC++6укр.doc