Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный технический университет Украины «Киевский политехнический институт»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

методичка 2 семестр интегралы

.pdf

Скачиваний:

Добавлен:

12.05.2015

Размер:

5.01 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 196 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

1. Функції кількох змінних

Якщо (x;y) (a;b), то

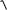
(x a)2 (y b)2 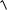2 cos2 2 sin2 0.

Задачу зводять до дослідження lim F( , ), де

F( , ) f (a cos ,b sin ).

1.3.3. Знайти lim(2x 5y) sin	3 .
x 0	x
y 0
Розв’язання. Оскільки (2x 5y) 0, коли		x 0,		y 0, і	sin		3	1, то за
							3
						x
						x
властивістю н. м. ф. маємо, що
lim(2x 5y) sin		3	0.
x 0		x
y 0

1.3.4.Знайти lim x2 y2 .

x0 x2 y2 y 0

Розв’язання. [Переходимо до полярних координат.]

x cos ,

y sin ;



x 0,		2		2
	x	2	y	2	0.
	x		y		0.
y 0

lim

cos2

sin2

cos2

sin2

cos 2 .

cos2

sin2

cos2

sin2

x 0 x2

x 0

y 0

Границя залежить від кута , тобто від способу прямування точки (x;y) до то-

чки (0; 0). А це означає, що функція f не має границі.

Коментар. Якщо б границя існувала, то вона не залежала від способу прямування точки (x;y) до точки (0; 0).

1.4.1. Знайти точки розриву функції z (x 1)2 (y 2)2 .

Розв’язання. [1.2.2.] Для заданої функції точками розриву можуть бути лише точки, де знаменник дорівнює нулеві:

x 1, (x 1)2 (y 2)2 0

y 2.

Оскільки

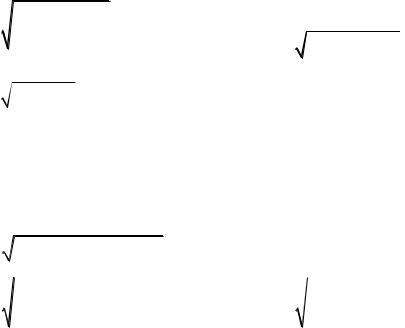
52	Розділ 1. Диференціальне числення функцій кількох змінних

lim	1		,

	(x 1)2 (y 2)2
x 1	(x 1)2 (y 2)2
y 2
то точка M0(1; 2) є точкою нескінченного розриву.
1.4.2. Знайти точки розриву функції z		x y		.
1.4.2. Знайти точки розриву функції z		x3 y3		.
		x3 y3

Розв’язання. Задана функція може мати розриви лише в точках, де знаменник дорівнює нулеві:

x3 y3 0 y x.

Отже, функція z має розриви на прямій y x.

Нехай x0 0, y0 0, x0

y0 . Тоді,

lim

x y

lim

x y

x x0 x3 y3

x x0 x2 xy y

y y0

0 0

Отже, точки прямої y x, x 0, — точки усувного розриву.

Із співвідношення

lim

x y

lim

xy y2

x 0 x3 y3

x 0 x2

y 0

випливає, що точка M0(0; 0) — точка нескінченного розриву.

Задачі для аудиторної і домашньої роботи

1.5.Знайдіть область означення функції і побудуйте її лінії рівня:

1) z	x2	y2	1;
	9	4

3) z 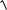4x y2 ;

5) z arcsin	x	arcsin(1 y);

y2

2)	z			1						;


		9 x2						y2
						x		2	y		2
						x			y
4)			1									;

	z ln
							4		9
							4		9
6)	z arccos							x	.
6)	z arccos				x			y	.
					x			y

1.6.Знайдіть область означення функції і побудуйте її поверхні рівня:

1) u

x2 y2 z2 R2 ;

2) u ln(1 x2

y2 z2 );

3) u

;

4) u

1. Функції кількох змінних

1.7.Знайдіть:

1) lim		xy		;


x 0	3		xy 9
y 0

3) lim(x y) sin 1 cos 1 ; x 0 x y

y 0

5) lim(1 x2 y2 )x2 y2 ;

x 0 y 0

1.8. Покажіть, що границя не існує:

1) lim x y ; x 0 x y

y 0

1.9.Знайдіть точки розриву функції:

1)z e x2 y2 ;

3) z y x2 ;

1.10. Знайдіть точки розриву функції:

1) u xyz1 ;

3) u x2 y2 z2 1 ;

lim

tg(x y)ex y

;

x2 y2

x 1

y 1

4) lim(x2

y2 ) arctg

;

x2 y2

x 0

y 0

x y

lim

y 5

2) lim

x 0 x2

y 0

2) z ex2 y2 ;

4) z

x2 y2 1

2) u

;

(y 1)

4) u

x2 y2 z2 1

Відповіді

1.7. 1) 6; 2)	e2		; 3)	0; 4)	0; 5) e; 6) e3.
		2

1.9. 1) точка розриву (0; 0); 2) лінії розриву — прямі y x; 3) лінія розриву — парабола

y x2; 4) лінія розриву — гіпербола x2 y2 1.

1.10. 1) поверхні розриву — площини x 0, y 0, z 0; 2) точка розриву (1; 1; 0);

3)поверхня розриву — однопорожнинний гіперболоїд x2 y2 z2 1 0;

4)поверхня розриву — двопорожнинний гіперболоїд x2 y2 z2 1 0.

54	Розділ 1. Диференціальне числення функцій кількох змінних

2. Похідні й диференціали функцій кількох змінних

Навчальні задачі

2.1.1. Знайти частинні похідні 1-го порядку функції z xe xy .

Розв’язання. [1.3.1.] [Знаходимо похідну за змінною x.]



zx (xe xy )x e xy xye xy .

[Знаходимо похідну за змінною y.]



zy (xe xy )y x2e xy .

Коментар. Знаходячи частинну похідну функції z xe xy за змінною x, вважаємо y сталою і використовуємо правила і формули диференціювання функцій однієї змінної.

Знаходячи частинну похідну функції z xe xy за змінною y, вважаємо x сталою і використовуємо правила і формули диференціювання функцій однієї змінної.

2.1.2. Знайти частинні похідні 1-го порядку функції u zxy .

Розв’язання. [1.3.1.]

ux yzxy ln z,uy xzxy ln z,uz xyzxy 1.

Коментар. Функція u залежить від трьох змінних x,y,z. Знаходячи частинні похідні за кожною змінною, інші дві вважаємо сталими.

2.2.1. Знайти частинні диференціали і повний диференціал 1-го порядку функ-

ції u ln(x2 y2 ).

Розв’язання. [1.4.5, 1.4.6.]

[1.4.6]

u u dx

dx;

d u

u dy

dy.

x2 y2

[1.4.5]

u dx

u dy

dy.

x2 y2

Коментар. У формулах для диференціалів диференціали незалежних змінних dx та dy є сталими:

dx x,dy y.

2. Похідні й диференціали функцій кількох змінних

2.2.2.

Знайти

диференціал

1-го

порядку

функції

у точці

M0(1;2;1).

Розв’язання. [1.4.6.]

[1.4.6]

dz.

;

(x2 y2 )2

M0 (1;2;1)

підставляємо: x 1,y 2,z 1

;

y2 )2

(x2

M0 (1;2;1)

1 .

M0 (1;2;1)

[Підставляємо знайдені похідні у формулу для диференціала.]

2dx 4dy 5dz .

M0 (1;2;1)

Знайти du

2.3.

, якщо u xy , x ln t,y sin t.

Розв’язання. [1.3.2.]

[1.3.2]

u dx

yxy 1 1 xy

ln x cost

x dt

y dt

sin t

(ln t)sin t 1

cost ln ln t (ln t)sin t .

2.4.

Знайти

та dz

, якщо z ln(ex ey ),y

1 x3 x;

Розв’язання. [1.3.3.]

[Знаходимо частинну похідну.]

ex ey

[Записуємо формулу для повної похідної і знаходимо похідну.]

[1.3.3]

z dy .

y dx

(x2 1) 1

x2e 3 x

2e 3

ex e

1 e

56	Розділ 1. Диференціальне числення функцій кількох змінних

2.5.Знайти zu , zv , якщо z x3 y3 3xy, x uv,y uv .

Розв’язання. [1.3.2.] [Визначаємо формули.]

[1.3.2]

z x

z y

x u

y u

[1.3.2]

z x

z y

x v

y v

[Обчислюємо всі потрібні похідні.]

3y 3u v

3 v

;

2 3x 3

3uv;

;

[Підставляємо знайдені похідні у формули.]

2 2

2 3

3u v

3uv

3 u v

2 2

3u v

3uv

2.6. Знайти zx , zy якщо x 2y 3z

ez .

2u ;

1 .

Розв’язання. [1.3.4.] [Записуємо співвідношення, яке задає неявну функцію у ви-

гляді F(x, y, z) 0.]

F(x,y, z) x 2y 3z ez .


z	[1.3.4]		Fx	1
					;
x			Fz	3 ez
	[1.3.4]
z		Fx		2
					.
y		Fy		3 ez

2.7.Знайти всі похідні 2-го порядку функції z xe xy .

Розв’язання. [1.3.5, 1.3.6.] [Знаходимо похідні 1-го порядку.] zx x (xe xy ) (1 xy)e xy ;

zy y (xe xy ) x2e xy.

[Знаходимо похідні 2-го порядку.]

2. Похідні й диференціали функцій кількох змінних

zyy

zxy

zyx

2 xy

((1

xy)e

) 2ye

xy e

;

x x

2 xy

3 xy

( x e

)

x e

;

y y

((1 xy)e

) 2xe

x ye

;

( x e

)

2xe

x ye

Коментар. Для функції двох змінних можна розглядати чотири похідні 2-го порядку. Якщо виконані умови теореми Шварца [1.3.6], то мішані похідні zxy

та zyx рівні.

2.8. Знайти диференціали 2-го та 3-го порядку функції u(x,y) ey sin x. Об-


числити їх у точці M0
числити їх у точці M0		;0 .

	2

Розв’язання. [1.4.7, 1.4.8.]

[Записуємо формулу для диференціала 2-го порядку функції двох змінних.]

[1.4.7]

d2u

x2 dx2 2

dxdy y2 dy2.

x y

[Знаходимо похідні 2-го порядку.]

2u ey

sin x;

ey cos x;

2u ey sin x.

x y

[Підставляємо знайдені похідні у формулу для диференціала.]

d2u ey sin xdx2 2ey cos xdxdy ey sin xdy2.

[Обчислюємо диференціал у точці M0.]

d2u(M

) ey sin xdx2 2ey cos xdxdy ey sin xdy2

dx2

dy2.

[Записуємо формулу для диференціала 3-го порядку функції двох змінних.]

[1.4.8]	3z dx3 3			3z			3z
d3z					dx2dy 3			dxdy2
							x y2
m 3	x3		x2 y
[Знаходимо похідні 3-го порядку.]
	3u ey cos x;					3u	ey sin x;
						x2 y
	x3
		3u		ey cos x; 3u			ey sin x.
		x y2
						y3

3z dy3.

58	Розділ 1. Диференціальне числення функцій кількох змінних

[Підставляємо знайдені похідні у формулу для диференціала.]

d3u ey cos xdx 3 3ey sin xdx2dy 3ey cos xdxdy2 ey sin xdy3.

[Обчислюємо диференціал у точці M0.]

d3u(M	0	) ey cos xdx 3	3ey sin xdx2dy 3ey cos xdxdy2	ey sin xdy3
	0
					M		;0
					M		;0
				0
						2

3dx2dy dy3.

Задачі для аудиторної і домашньої роботи

2.9.Знайдіть частинні похідні і повний диференціал функції:

1) z x3y y3x;			2) z	x3	y3	;
				x2	y2

3) z ln x		;	4) z xy ;
	x2 y2
5) x cos ;			6) y	t	t sin .

2.10. Знайдіть частинні похідні і повний диференціал функції:

1) u xyz;

2) u x3 yz2 3yx x z;

3) u xyz ;

4) u x

2.11.

Знайдіть du(M0 ), якщо:

1) u

2) u ln arcsin(x y3 ), M0

; 0 ;

, M0(1;1);

3) u

, M

0(3; 4;5);

4) u xy

, M0

(1;1;1).

2.12.

Знайдіть du

, якщо:

1) u ex 2y, x sin t,y t3;

2) u arcsin(x y), x 3t,y 4t3;

3) u xyz,x t2 1,y ln t, z		tg t;
4) u yz	, x et ,y ln t, z t2	1.
x

			2. Похідні й диференціали функцій кількох змінних						59
2.13.	Знайдіть		dz	та z , якщо:
			dx	x
		z arctg(xy),y ex ;				z arcsin x ,y
	1)	z arctg(xy),y ex ;			2)	z arcsin x ,y			x2 1;
							y
	3)	z xy, y (x);			4)	z arctg	x 1	, y e(x 1)2 .
	3)	z xy, y (x);			4)	z arctg		, y e(x 1)2 .
							y
2.14.	Знайдіть		z	, z якщо:
			u	v

1) z x2 ln y,x uv ,y 3u 2v; 2) z x2 y2 , x uv ,y u ln v;

3) z xy yx , x u2 v2, y u2 v2 ;

4)z x sin y y cos x, x uv , y uv.

2.15.Знайдіть dz, якщо:

1)	x2e2z z2e2x		0;	2) z sin x cos(x z) 0;
3)	xz ez y x3		y3 0;	4) yz arctg(xz).
2.16. Знайдіть d2u,		якщо:
	1
	1
1) u 3 (x2		y2 )3 ;		2) u arcsin(xy);
3) u (x y)exy ;				4) u x ln y ;
				x
5) u xy yz zx;				6) u exyz .

2.17.Знайдіть d2u(0, 0, 0), якщо u x2 2y2 3z2 2xy 4xz 2yz.

2.18.Знайдіть вказані похідні:

2			3z					3z
1) z exy	,				;		2) z ln(x2 y2 ),			;
1) z exy	,	2		y	;		2) z ln(x2 y2 ),	x y	2	;
		x		y				x y
3) u f (x, y, z), z (x, y),						2u	;
3) u f (x, y, z), z (x, y),						x y	;
						x y

60	Розділ 1. Диференціальне числення функцій кількох змінних

4) u f (x, y, z), x s2 t2, y s2 t2, z 2st, us , ut .

2.19.Замінюючи повні прирости функцій їхніми диференціалами, обчисліть наближено:

1, 982 1, 012;

2) 2, 0032 3, 9983

1, 0022.

Відповіді

2.9. 1) zx 3x2y y3, zy x3

3y2x;

2) zx

x 4 3x2y2 2xy3

, zy

y4 3x2y2 2x3y

;

(x2 y2)2

(x2 y2 )2

3) zx

, zy

;

x2 y2

x2 y2 x

x2 y2

4) zx yxy 1, zy xy ln x.

5) x cos , x

sin ; 6)

sin , y

t cos .

2.10. 1) u

yz, u

xz, u xy;

3x2 3y 1, u

3x,

2yz 1;

3) u

yzxyz 1,

zxyz ln x, u

yxyz ln x;

4) u

1;u

ln x;u

ln x.

2.11. 1) du(M0 ) dx 2dy; 2)

du(M0 ) 6 dx;

du(M0 )

dy 1 dz;

4) 2dx ln 4 dz.

2.12. 1) ex 2y(cos t 6t2);2)

3 12t2

;

1 (x

y)2

2tyz

;

x(z 2yt2) yztet

cos2 t

tx2

2.13.

ex (x 1)

; 2)

;

x2e2x

2y2

y2 x2

y 1

;

(x) ln x

, dz

y(1 2(x 1)2)

2 (x 1)2

y2 (x 1)2

2.14. 1) zu

ln(3u 2v)

3u2

, zv

2u2

ln(3u 2v)

2u2

;

v2(3u

2v)

v2(3u 2v)

2) zu

vuv 1

ln v, zv

xuv

ln u

y u

;

x2 y2

x2 y2 v

<<< < Предыдущая 1 2 3 4 56 / 196 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.20194.29 Mб92Методическое пособие для барменов.doc
#
09.11.2019540.16 Кб2Методическое____пособие_инструктору_АФФ.doc
#
11.11.2019304.13 Кб9методичка 5 курс (правильная).doc
#
17.03.20161.6 Mб139Методичка (дискретка).pdf
#
05.11.2018265.73 Кб5методичка 2 курс спецфакультет (1).doc
#
12.05.20155.01 Mб42методичка 2 семестр интегралы.pdf
#
12.11.2019111.71 Кб2Методичка 4 курс МП ММІ .doc
#
12.05.2015265.22 Кб37МЕТОДИЧКА 5 КУРС.doc
#
09.11.2019181.25 Кб0Методичка 5курс (1 часть).doc
#
09.11.2019143.36 Кб2Методичка 5курс (2 часть).doc
#
20.12.2018287.74 Кб1Методичка VC++6укр.doc