методичка 2 семестр интегралы

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный технический университет Украины «Киевский политехнический институт»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Рис. до зад. 6.1

Рис. до зад. 6.1

.pdf

Скачиваний:

Добавлен:

12.05.2015

Размер:

5.01 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 199 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

												6. Застосування визначеного інтеграла																											81
5.4. 1)		4 ;	2) 1; 3)				0; 4)				. 5) 64; 6) 8; 7)								5			;	8)			t .
		3						2											6							2
												3) 0; 4) sin					x			1							1	.
5.5. 1) ln x; 2)							1 x 4 ;										x			1				sin			1
5.5. 1) ln x; 2)							1 x 4 ;												x2					sin
													2				x		x2								x2
5.6. 1)		1 2 ;		2)	(9 4							3) 1 ln				3	; 3) 6 2e; 4)													.
			e				36						2			2
5.7. 1)		8	; 2)	5			; 3)	5			; 4)			8	; 5)		0; 6)				35				.
5.7. 1)			; 2)				; 3)				; 4)				; 5)		0; 6)				35				.
		15		256			16						35									64
		32																				2										8
							3 3									2										3									1		7 3
							3 3									2										3									1		7 3
5.8. 1)			; 2) 8					;				3)																		; 4)				5)				8
														2				ln															;						;
		3					2							2				ln														15	;		32		2		;
		3					2									3						1				2						15			32		2
																3						1				2
												; 8) 2
	3																			2				arctg					1		; 10)					.
6)	3	ln(2				3); 7)											; 9)			2									1
6)	2	ln(2				3); 7)			6								; 9)																	3
	2								6				32									5								5				3	3
5.9. 1) 2 I								2					2 .
5.9. 1) 2 I					5; 2)			2		I			2 .
								9					7

6. Застосування визначеного інтеграла

Навчальні задачі

6.1.

Знайти площу фігури, обмеженої кривими y ex 1,

y e2x 3,

x 0 .

Розв’язання. [2.4.2.]

[Записуємо формулу, виходячи із шуканого застосування інтеграла.]

Площу

фігури, обмеженої лініями y f (x),y g(x),

x a,x b знаходять за формулою

y e2x 3

[2.4.2] b

y ex 1

f (x) g(x)

dx.

Знаходимо точку перетину графіків функцій:

ln 2

e2x 3 ex 1; t ex .

На відрізку [0;ln 2] маємо ex 1 e2x 3 :

ln 2								ln 2
S	(ex 1) (e2x 3) dx (ex 2 e2x )dx
0							ln 2	0
				1					1

		x	2x		e	2x		2 ln 2		.
	e		2x		e			2 ln 2		.
				2					2
				2			0		2
							0

82	Розділ 2. Визначені інтеграли

6.2.1. Знайти площу області, обмеженої еліпсом x2 a2

Розв’язання. [2.4.4.]
Параметризуємо рівняння еліпса:
	a cost,
x	a cost,
		t [0;2 ].
		t [0;2 ].
y b sint,

y2 1,a,b b2

Площу криволінійної трапеції, обмеженої кривою, заданою

	x(t),
x	x(t),
		t [t ;t		] знаходять за формулою
	y(t),	t [t ;t		] знаходять за формулою
y	y(t),	1	2


				[2.4.4]	t2
				S	y(t)x (t)dt
					t1

Ураховуючи симетрію фігури, одержимо:

параметрично

a x

S 4	2	2		1 ab.	Рис. до зад. 6.2.1
S 4	b sint( a sint)dt	4ab sin2 tdt 4ab		1 ab.

	0	0	2	2
	0	0

6.2.2.Знайти площу фігури, y 3(0 x 4 ,y

x 2(t sint),

обмеженої циклоїдою та прямою

y 2(1 cost)

3).

Розв’язання. [2.4.4.]
Площу криволінійної трапеції, обмеженої кривою,	y	y 3
що задана параметрично знаходять за формулою		y 3
що задана параметрично знаходять за формулою
t2
S y(t)x (t)dt .
S y(t)x (t)dt .	O	x1	x2	x
t1	O	x1	x2	x

Рис. до зад. 6.2.2

Обмеження 0 x 4 вказує на те, що розглядають лише І арку циклоїди. Пряма перетинає циклоїду в точках з абсцисами x1 та x2 . Площу шуканої фігури

можна знайти віднявши від площі під циклоїдою в межах x1 x x2 площу прямокутника 3(x2 x1). Знайдімо значення параметра в точках перетину прямої і циклоїди:

	cost),
y 2(1	cost),						1
			3 2(1 cost) cost				1	;
			3 2(1 cost) cost					;
							2
y 3							2
		2 ,t			4
	t	2 ,t		2	4	(0 t 2 ).
	1	3		2	3
		3			3

6. Застосування визначеного інтеграла

			2			4				4			8

x		2		sin	2		3, x		2		sin	4		3.
x		2		sin			3, x		2		sin			3.
	1		3		3	3		2		3		3	3
			3		3	3				3		3	3

		4

S	3		2 3	4 6 3.
S	3		2 3	4 6 3.
		3
		3

					4 3						4 3				1 cos 2t
S		4						2	4			2 cost			1 cos 2t
S		4				(1 cost) dt			4		1	2 cost				dt

											2 3				2
					2 3						2 3				2
			3				1			4 3			9
										4 3

														3
	4			t 2 sint							4				4 9	3.
	4		2	t 2 sint			4	sin 2t			4		4		4 9	3.
			2				4						4

										2	3
										2	3

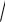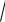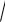S (4 93) (4 63) 33.

6.3.Знайти площу фігури, обмеженої кривими: 4 cos 3 , 2 ( 2).

Розв’язання. [2.4.3.]
Площу фігури, обмеженої трипелюстковою розою та колом
знаходимо, враховуючи симетрію:
						S 3S ,															9
																					9
де																			O		P
де		.
Знайдімо за якого значення кута (для розглядуваної пелюс-
тки), перетинаються коло і роза:

	2,														1
						4 cos 3				2 cos 3					1	.		Рис. до зад. 6.3.
				4 cos ,		4 cos 3				2 cos 3						.		Рис. до зад. 6.3.
				4 cos ,											2
															2

						3 2 k,k ; .
								3						1,2			9
								3									9
								S		S S ,
де S — площа кругового сектора, S													— площа «розового» сектора.
				9							9								9
			1			2						1	cos 6					sin 6
S					16 cos 3 d 16										d
S			2		16 cos 3 d 16								2		d		8	6
			2	9							0		2					6		0
									1					8		2 3
									1	sin		2		8		2 3	.
						8				sin							.
							9		6			3		9		3
							9		6			3		9		3

	S			1	9 4d 4			9		4 .
	S			1	9 4d 4			9		4 .
				2				0		9
					9

S		8 2 3				4 4			2 3 .
			9		3	9	9			3
			9		3	9	9			3

84	Розділ 2. Визначені інтеграли

6.4. Обчислити об’єм тіла , обмеженого еліпсоїдом x2	y2		z2	1,

a2	b2	c2

a 0,b 0,c 0.

Розв’язання. [2.4.5.]

Об’єм тіла за відомою площею перерізу його площиною, перпендикулярною до осі Ox знаходять за формулою:

[2.4.5] b

V S(x)dx

Кожний переріз тіла, обмеженого еліпсоїдом, площи-

ною x x0, a x0 a, є фігурою, обмежена еліпсом:

та c

з півосями

a2 x2

a x a.

Площа фігури (задача 6.2.1):

S(x

), a

)

Отже, позначаючи x0

через x, a

x a,

одержимо:

V S(x)dx bc2 (a2 x2)dx 2 bc2 (a2 x2)dx

a x

Рис. до зад. 6.4

x0 a.

43 abc.

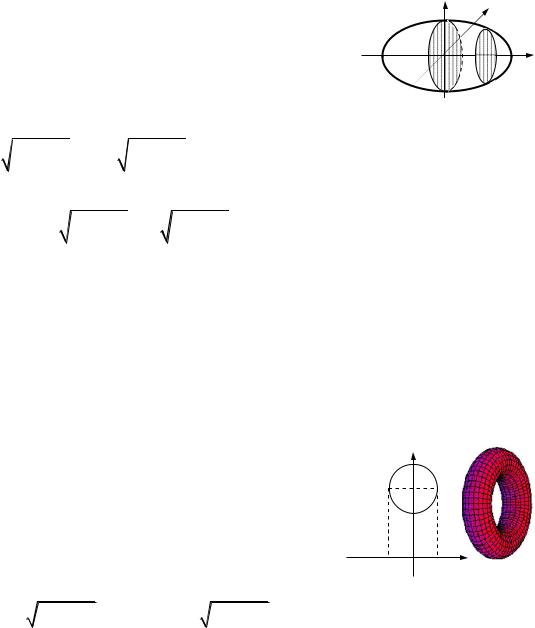
6.5.Обчислити об’єм, обмежений тором і площу тора, утвореного обертанням кола x2 (y b)2 a2 навколо осі Ox (b a).

Розв’язання. [2.4.6, 2.4.7.]

1. Об’єм тіла, одержаного обертанням криволінійної трапеції навколо осі Ox знаходять за формулою

V f 2(x)dx.

Об’єм тіла, утвореного обертанням криволінійних трапецій, обмежених зверху лініями

y b a2	x2	та y	2	b a2	x2
1			2

знаходимо за формулою:

a O a x

Рис. до зад. 6.4.2

6. Застосування визначеного інтеграла				85
a		a
a		a
Vт V2 V1 (b a2 x2 )2dx (b a2 x2 )2dx
a		a
a		a2
4 b	a2 x2dx 4 b	a2	2 a2b.
a		2
a

2. Площу поверхні обертання, утвореної обертанням кривої y f(x), x [a;b], навколо осі Ox знаходять за формулою

[2.4.7] b

Q 2 f (x)1 (f (x))2dx.

Площу поверхні обертання, утвореної обертанням ліній

y b a2	x2	та y	2	b a2	x2
1			2

знаходимо за формулою:

Q Q1 Q2 2 (b a2 x2 ) 1

2 (b a2

x2 ) 1

4 ba arcsin x

4 ba

4 2ab.

a2 x2

6.6.Матеріальна точка M рухається прямолінійно зі швидкістю

v(t) 3t2 2t 1 м/с.

Знайти шлях, який пройде точка за проміжок часу [0;3].

Розв’язання. [2.4.10.]

Шлях, пройдений матеріальною точкою із швидкістю v v(t) за проміжок ча-

су [t1;t2 ] знаходять за формулою

s v(t)dt.

Отже,

S (3t2 2t 1)dt (t3 t2 t) |30 39 м.

6.7.Знайти роботу, яку треба витратити, щоб розтягнути пружину на 10 см, як-

що відомо, щоб розтягнути пружину на 1 см треба прикласти силу в 1 кН.

Розв’язання.

86	Розділ 2. Визначені інтеграли

Нехай під дією сили F(x) матеріальна точка рухається вздовж прямої Ox. Роботу цієї сили на ділянці шляху [a;b] визначають за формулою

A F(x)dx.

За законом Гука, сила F, що розтягую пружину, пропорційна її розтягу, тобто

F kx,

де x — розтяг пружини (в метрах), k — коефіцієнт пропорційності. Оскільки за умовою при x 0, 01 сила F 1000 Н, то

1000 0, 01k k 105.

Отже,

0,1

A 105xdx 50000x2 |00,1 500 Дж.

Задачі для аудиторної і домашньої роботи

6.11.Знайдіть площу фігур, обмежених:

1)параболами y2 8x 16 та y2 24x 48;

2)колом x2 y2 9 і параболою y2 8x;

6.12.Знайдіть площу фігур, обмежених лініями:

1) y x(x 1)2,y 0;

2) x y2(y 1),x 0;

3) y ex ,y e x,x 1;

4) y

6.13. Знайдіть площу фігури, обмеженої:

x a(t sint),

1) однією аркою циклоїди

y a(1 cost)

x a cos3 t,

2) астроїдою

y a sin3 t.

tg x,y 23 cos x, x 0.

та віссю абсцис;

6. Застосування визначеного інтеграла

6.14. Знайдіть площу петлі лінії:

	2			2
	2	,	x t	2	1,
x 3t		,	x t		1,
1)			2)		t.
y 3t t3;			y t3		t.

6.15.Знайдіть площу фігури, обмеженої:

1)двопелюстковою розою a sin 2 ;

2)п’ятипелюстковою розою a cos 5 ;

3)лініями 3 cos 4 та 2 cos 4 ;

4)лінією 2 cos 2 , що лежить поза лінією 2 sin ;

5). лемніскатою Бернуллі (x2 y2)2 a2(x2 y2).

6) лемніскатою Бернуллі (x2 y2)2 a2(x2 y2), яка лежить усередині

кола x2 y2 a2 . 2

6.16.Знайдіть об’єм тіла, утвореного обертанням фігури, обмеженої лініями, навколо осі Ox :

1) y x3,x 0,y 8;	2) y	2	,y 0,x 0,x 1.

		x2
	1

6.17.Крива обертається навколо осі Ox. Обчисліть площу поверхні обертання:

1) y2 x,x [0;4];

2) y sin x,x [0; ];

6.18.1. Знайдіть об’єм кулі радіусом R.

2. Знайдіть об’єм конуса з радіусом основи R і висотою H.

6.19.1. Швидкість прямолінійного руху матеріальної точки v(t). Знайдіть шлях, який пройде точка від початку руху до повної зупинки, якщо:

			1) v te 0,01t м/с;												2) v 4te t2					м/с.
Відповіді
			32																	2 4			6 4
									9 arcsin	8			9 9 arcsin			8	; 3.
6.11. 1)					6; 2)		S	1		8	, S	2				8		S	1		,S	2		;
6.11. 1)					6; 2)		S				, S							S			,S			;
				3					2	3				2		3				3			3
				3					2	3				2		3				3			3

4)S		S				1			ln 3 2 arcsin		2	0, 46,S			2( S ).
4)S	1	S		3					ln 3 2 arcsin			0, 46,S		2	2( S ).
	1			3			2				3			2		1
							2				3

88	Розділ 2. Визначені інтеграли

6.12. 1).	1	;	2)	1	; 3) e					1 2;		4)		1	ln		3	.
6.12. 1).	12	;	2)		; 3) e					1 2;		4)	3		ln	2		.
	12		12							e			3			2
6.13. 1) 3 a				3 a2
6.13. 1) 3 a			2; 2)		8			.
					8
	72					8		.
6.14. 1)	72		3; 2)			8
6.14. 1)	5		3; 2)		15
	5				15
	a	2		a			2			37
															51 3

																										3
																				2		2
6.15. 1)			; 2)					; 3)			5		3;		4)				; 5) a		; 6) a		1				.
	4				4					6						16								6
	4				4					6						16								6	2

6.16. 1)	768		; 2)		2			2 .
	7							2
6.17. 1)	52	; 2) 2 (
6.17. 1)	52	; 2) 2 (						2 ln(1				2)).
	3
6.18. 1)	4 R3; 2)					R2H			.
6.18. 1)	4 R3; 2)								.
	3							3
6.19. 1) 104 м; 2) 2 м.

7. Обчислення і дослідження невластивих інтегралів

Навчальні задачі

1 2x

7.1.1. Обчислити інтеграл 1 x2(x 1)dx або довести його розбіжність.

Розв’язання. [2.5.1.] Маємо невластивий інтеграл 1-го роду.

1 2x

[2.5.1]

1 2x

lim

x (x 1)

A 1 x (1 x)

2x 1

x x 1

x(x

(x 1)

x 1 x

x 1

x(x 1)



lim

x 1

lim ln

ln 2 1

ln 2 1.

A 1

1 A 

x 1

Коментар. Проміжок інтегрування нескінчений, і підінтегральна функція на ньому неперервна.

Інтеграл від суми дорівнюватиме сумі інтегралів лише в разі їхньої збіжності. Границя від суми тут теж не дорівнює сумі границь.

7. Обчислення і дослідження невластивих інтегралів

7.1.2. Обчислити інтеграл xe axdx, (a 0), або довести його розбіжність.

Розв’язання. [2.5.1.] Маємо невластивий інтеграл 1-го роду.

u x

du dx

xe axdx

lim

xe axdx

A 0

dv e

v a e

lim



lim

Інтеграл збігається.

Коментар. За правилом Бернуллі — Лопіталя.

5dx

7.1.3.Обчислити інтеграл x ln x або довести його розбіжність.

Розв’язання. [2.5.2.] Оскільки x 1 є точкою нескінченного розриву, то маємо невластивий інтеграл 2-го роду.

5	dx	[2.5.2]		5	d ln x
			lim			lim ln	ln x

	x ln x				ln x
1			0	1		0

	lim ln ln 5 ln ln 1 .
		0

Інтеграл розбігається.

Коментар. Межі інтегрування є скінченними. Досліджуючи невластивий інтеграл за означенням, відступаємо всередину проміжку інтегрування.

2 3

7.1.4. Обчислити інтеграл 1 3 x 9x2 1 або довести його розбіжність.

Розв’язання. [2.3.5.] Оскільки x 13 є точкою нескінченного розриву, то має-

мо невластивий інтеграл 2-го роду.

90	Розділ 2. Визначені інтеграли

2 3		dx						x	1	,			x		1		2			3				dt
2 3									1											3

									t
											dt				3		3
													t		3		3
	x 9x2			1				dx				.					3							9
1 3																	2			3 2 t							1
											t2						2
																							t2
3																				3			t2
3		dt					t 3		точка											3						dt
		dt							точка							lim										dt
																lim
3 2		9 t2					нескінченного розриву											0			3 2				9 t2
3 2		9 t2																			3 2				9 t2
		t	3																			1
		t	3																			1
lim arcsin																	arcsin													.
lim arcsin		3	3 2		lim arcsin 1												arcsin					2					2	6	3	.
0		3	3 2											3								2					2	6	3
0						0
															xdx
7.2.1. Дослідити на збіжність інтеграл															xdx				.
7.2.1. Дослідити на збіжність інтеграл																			.
												0		x5 1

Розв’язання. [2.5.5, 2.5.9.] [Плануючи використати ознаку порівняння, розбиваємо невластивий інтеграл 1-го роду на суму двох інтегралів так, щоб точка 0 не належала проміжку інтегрування невластивого інтеграла.]

	xdx	1	xdx		xdx
						.

0	x5 1	0	x5 1	1	x5 1

Перший доданок — визначений інтеграл. А другий — невластивий інтеграл 1-

го роду

xdx

Дослідімо

за ознакою порівняння.

x5 1

f (x)

0, x [1;

);

x5 1

f (x)

g(x), x

x5 2

x3 2

xdx

Оскільки

збігається[2.5.9], то

збігається за ознакою порів-

3 2

x5 1

няння.

xdx

Інтеграл збігається як сума визначеного і збіжного невластивого

0 x5 1

інтеграла.

Коментар. Точка x 1 в якій підінтегральна функція стає необмеженою, не належить проміжку інтегрування.

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 199 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.20194.29 Mб92Методическое пособие для барменов.doc
#
09.11.2019540.16 Кб2Методическое____пособие_инструктору_АФФ.doc
#
11.11.2019304.13 Кб9методичка 5 курс (правильная).doc
#
17.03.20161.6 Mб139Методичка (дискретка).pdf
#
05.11.2018265.73 Кб5методичка 2 курс спецфакультет (1).doc
#
12.05.20155.01 Mб42методичка 2 семестр интегралы.pdf
#
12.11.2019111.71 Кб2Методичка 4 курс МП ММІ .doc
#
12.05.2015265.22 Кб37МЕТОДИЧКА 5 КУРС.doc
#
09.11.2019181.25 Кб0Методичка 5курс (1 часть).doc
#
09.11.2019143.36 Кб2Методичка 5курс (2 часть).doc
#
20.12.2018287.74 Кб1Методичка VC++6укр.doc