27. 4.4. Векторное произведение векторов

Определение. Тройка векторов 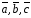называется правой (левой), если из конца вектора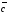кратчайший поворот от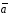к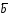виден совершающимся против часовой стрелки (по часовой стрелке).

Определение. Векторным произведением и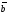называют вектор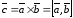, удовлетворяющий условиям:

1) ;

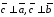2) ;

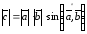3) векторы 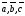, взятые в указанном порядке, образуют правую тройку.

Геометрический смысл модуля векторного произведения векторов.

Так как 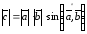, то модуль векторного произведения численно равен площади параллелограмма, построенного на векторах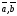как на сторонах.

Свойства векторного произведения векторов:

1) ;

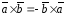2) ;

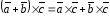3) ;

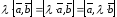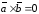
4) если 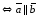(необходимое и достаточное условие параллельности векторов).

Если векторы заданы в координатной форме: ,, то

Задача. Найти площадь треугольника с вершинами в точках . Вычислить длину высоты, опущенной из вершиныB.

Решение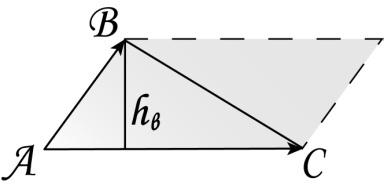

, ;

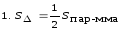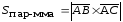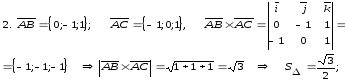
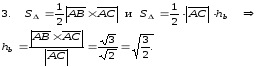
Ответ: кв. ед,.

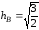28. 4.5 Смешанное произведение векторов

Определение. Смешанным, или векторно-скалярным, произведением векторо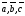в называют число, равное векторному произведению векторов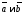, скалярно умноженному на, то есть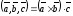

Геометрический смысл смешанного произведения векторов состоит в том, что модуль смешанного произведения векторов 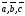численно равен объёму параллелепипеда, построенного на этих векторах как на сторонах:

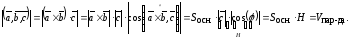
Также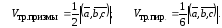

Свойства смешанного произведения векторов:

1) смешанное произведение не меняется при циклической перестановке его сомножителей ;

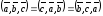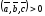2) если – правая тройка, тои если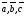– левая тройка, то.

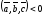Если векторы заданы в координатной форме: ,

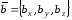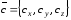, , то.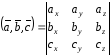

Необходимым и достаточным условием компланарности трёх векторов 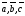является равенство нулю их смешанного произведения:компланарны.

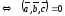29. Лекция 5. Координатный метод

5.1. Системы координат на плоскости

5.2. Системы координат в пространстве

5.1. Системы координат на плоскости

Система координат на плоскости – это правило, которое устанавливает взаимно однозначное соответствие между точками плоскости и упорядоченными парами чисел, которые называют координатами заданной точки.

Аффинная система координат на плоскости

Репер <О; ,> на плоскости задает систему координат следующим образом. Каждая точка М определяет вектор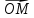, который определяет упорядоченную пару чисел (х,у) равенством 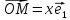+у . Числах,у являются координатами точки М, что может быть подчеркнуто записью М=М(х,у). Такая система координат называется косоугольной или аффинной системой координат на плоскости. Первая координата точки в такой системе координат называется абсциссой, а вторая – ординатой точки.

Ось, задаваемую точкой О и вектором 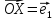называютосью абсцисс; ось, задаваемую Точкой О и вектором , называютосью ординат.

Если при взгляде на плоскость кратчайший поворот от оси абсцисс доь оси ординат осуществляется против хода часовой стрелки, то говорят, что система координат правая. Если же такой поворот осуществляется по ходу часовой стрелки, то такая система координат – левая. Если угол между осями координат прямой, то система координат называется прямоугольной декартовой системой координат на плоскости.

а) б) у в) 0 х

у

М(х,у)

е₂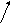

0 х у

а) аффинная система координат,

б) правая прямоугольная система координат,

в) левая прямоугольная система координат.

Полярная система координат

На плоскости определена полярная система координат, если заданы:

1. Числовая ось(называется полярной осью),

2. Направление вращения в плоскости, считаемое положительным.

Полярная система координат каждой точке М ставит в соответствие её полярные координаты ρ,φ, а именно:

1. Угол наклона φ вектора к полярной оси (т.е. угол поворота от вектор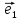а , задающего полярную ось, до вектора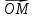в положительном направлении, этот угол называют полярным углом точки М);

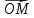
2. Расстояние ρ точки М от начала О (т.е. длина вектора 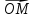, её называют полярным радиусом точки М),

М(ρ,φ)

φ

1. р

у

М(ρ,φ)

φ

0 р

Пусть заданы полярная и правая декартова системы координат, причем полярной осью служит ось абсцисс, а полюс О совмещен с началом О декартовой системы координат. Тогда между декартовыми координатами (х,у) и полярными координатами (ρ,φ) точки М на плоскости существует связь:

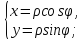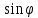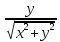и =,=, ρ=.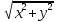

Точка О в полярной системе координат особая, для этой точки ρ=о, а φ не определено. Для всех остальных точек плоскости полярный радиус ρ>о, а полярный угол 0φ