20. 3.2. Собственные векторы и собственные значения матрицы

Пусть дана квадратная матрица А порядка n

Определение 1. Всякий ненулевой вектор Х, удовлетворяющий условию А·Х = λ·Х называется собственным вектором матрицы А, а соответствующее ему число λ – собственным значением матрицы А.

А·Х - λ·Х = 0, А·Х - λ·Е·Х = 0, ( А - λ·Е )· Х = 0,

где Е – единичная матрица, а вектор Х =.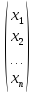

Матричное уравнение ( А - λ·Е )· Х = 0 имеет вид при переходе к покоординатному равенству:

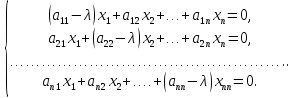(1)

Нас интересуют ненулевые решения однородной системы, поэтому приравняем определитель однородной системы к нулю: det ( A – λE)=0

или 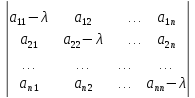= 0 (2)

Левая часть уравнения (2) называется характеристическим многочленом матрицы А: det ( A – λE). Это многочлен n – ой степени, он может иметь не более n действительных корней.

Действительные корни этого многочленаявляются собственными значениями матрицы А.

При последовательной подстановке в систему (1) для каждого λ находится ненулевое решение однородной системы (2) – собственный вектор линейного преобразования, заданного матрицей А.

Алгоритм нахождения собственных векторов

1. Составить матрицу А- λЕ и характеристическое уравнение det ( A – λE)=0.

2. Найти корни характеристического уравнения :.

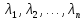3. Подставить значение корня 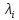в однородную систему (2) и найти соответствующий собственный вектор.

Пример. Найти собственные векторы и собственные значения матрицы

А =

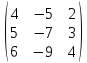
Решение

Составим матрицу А- λЕ =и перейдем в соотношении ( А - λ·Е )· Х = 0 к покоординатному равенству

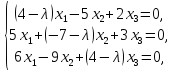(3)

где 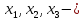координаты собственного вектора Х.

Составим характеристическое уравнение матрицы А для нахождения собственных значений:

det ( A – λE) = 0 или .

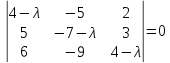Имеем det ( A – λE) = (4-λ)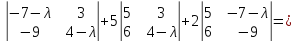

=- .

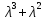Характеристическое уравнение - 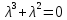имеет действительные корни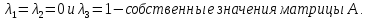

Найдем собственный вектор 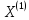, отвечающий собственному значению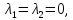для чего это значение λ = 0 подставим в однородную систему (3)

При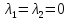определитель этой системы равен нулю, поэтому однородная система имеет бесконечное множество ненулевых решений. Найдем их методом Гаусса

4С₂ – 5С₁→С₂^/ С₃-С₂→С₃^/

2С₃ - 3С₁ →С₃^/

Получим равносильную систему трапецеидального вида:

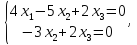
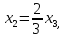
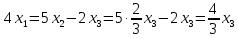или

Положим х₃ = 3t, тогда х₂= 2 t, х₁= t, получим собственный вектор

, где t.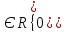

Рассуждая аналогично, получим при

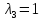
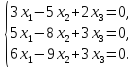
Найдем ненулевые решения этой системы

С₃:3→С₁^/ 2С₂-5С₁→С₂^/ С₃-С₂→С₃^/

С₁→С₃^/ 2С₃-3С₁→С₃^/

Имеем однородную систему 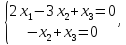откуда следует

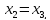2х₁ = 3х₂-х₃=3х₃-х₃=2х₃ или .

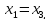Положим получим собственный вектор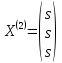, гдеs.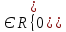

Ответ:

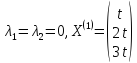, где t;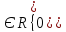

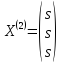, , гдеs.

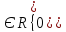21. 3.3. Модель Леонтьева многоотраслевой экономики

Основной задачей при математическом моделировании экономических процессов является задача создания модели межотраслевого баланса. Модель эта называется моделью Леонтьева (по имени ее создателя) и активно используется для управления народным хозяйством.

Предположим, что рассматривается n отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления. Рассмотрим процесс производства за некоторый период времени (например, год).

Введем следующие обозначения:

x_i — общий (валовый) объем продукции i-й отрасли 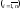за данный промежуток времени;

x_ij — объем продукции i-й отрасли, расходуемой j-й отраслью в процессе производства ;

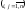y_i — объем продукции i-й отрасли, предназначенный к потреблению в непроизводственной сфере — объем конечного потребления. Этот объем составляет обычно более 75% всей производственной продукции. В него входят создаваемые в хозяйстве запасы, личное потребление граждан, обеспечение общественных потребностей (просвещение, наука, здравоохранение, развитие инфраструктуры и т.д.), поставки на экспорт.

Указанные величины можно свести в таблицу.

Производственное потребление	Конечное потребление	Валовый выпуск
х11 х12 ... х1n x21 x22 ... x2n .............................. xn1 xn2 ... xnn	y1 y2 ... yn	x1 x2 ... xn

Так как валовый объем продукции любой i-й отрасли равен суммарному объему продукции, потребляемой n отраслями, и конечного продукта, то

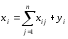
(1)

Уравнения (1) называются соотношениями баланса. Будем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в (1), имеют стоимостное выражение.

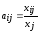
Введем коэффициенты прямых затрат 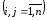, показывающие затраты продукцииi-й отрасли на производство единицы продукции j-й отрасли.

Можно полагать, что в некотором промежутке времени коэффициенты a_ij будут постоянными, это означает линейную зависимость материальных затрат от валового выпуска, т.е.

,

вследствие чего построенная на этом основании модель межотраслевого баланса называется линейной. Соотношения баланса (1) примут вид:

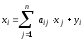
(2)

или в матричной записи

Х = А · Х + У, (3)

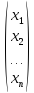где , Х = , У = ,

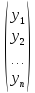А — матрица прямых затрат, Х — вектор валового выпуска, У — вектор конечного потребления.

Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска X, который при известной матрице прямых затрат А обеспечивает заданный вектор конечного потребления У. Перепишем уравнение (3) в виде Х – АХ = У, или Е · Х – А · Х = У, (Е – А) ·Х = У, откуда

Х = (Е – А)^–1 ·Y. (4)

Матрица (Е – А)^–1 называется матрицей полных затрат. В соответствии с экономическим смыслом задачи значения x_i должны быть неотрицательными при y_i  0 и a_ij  0, где .

Матрица А  0 называется продуктивной, если для любого вектора У  0 существует решение Х  0 уравнения (3). В этом случае модель Леонтьева называется продуктивной.

Существует несколько критериев продуктивности матрицы А.

Теорема 1. Матрица А продуктивна тогда и только тогда, когда матрица (Е – А)^–1 существует и ее элементы неотрицательны.

Теорема 2. Матрица А с неотрицательными элементами продуктивна, если сумма элементов по любому ее столбцу (строке) не превосходит единицы:

,

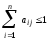причем хотя бы для одного столбца (строки) эта сумма строго меньше единицы.

Пример

№ п/п	Отрасль	Потребление			Конечный продукт, У	Валовый выпуск, Х
		1	2	3
1.	Добыча и переработка углеводородов	5	35	20	40	100
2.	Энергетика	10	10	20	30	70
3.	Машиностроение	20	10	10	10	50

Решение

_{1. По таблице баланса трех отраслей промышленности составим матрицу} А прямых затрат А = (a_ij), где ,

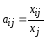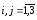
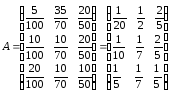
2. Проверим продуктивность матрицы А (по теореме 2)

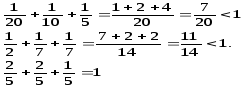
Так как сумма элементов по любому столбцу не превосходит единицы, и есть столбец, в котором сумма элементов меньше 1, то матрица А продуктивна.

3. Найдем матрицу полных затрат (Е – А)^–1. Составим матрицу:

.

Вычислим определитель матрицы Е – А:

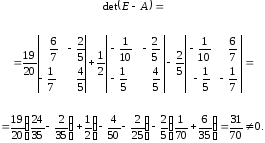
Построим матрицу алгебраических дополнений матрицы Е – А = В:

.

.

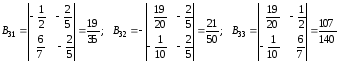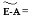
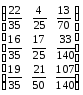
Союзная матрица

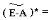
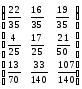
Матрица полных затрат

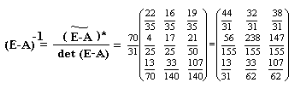
Проверка:

4. Найдем объем валового выпуска Х_* по каждой отрасли, если конечное потребление У увеличить по отраслям соответственно на 30, 10 и 50%, тогда конечный продукт 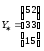. Согласно формуле (4)

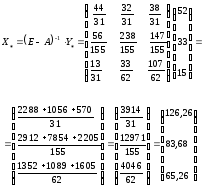
Таким образом, чтобы обеспечить заданное увеличение компонент вектора конечного продукта 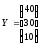соответственно на 30, 10, 50% необходимо увеличить соответствующие валовые выпуски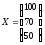добычу и переработку углеводородов на 26,26%, уровень энергетики на 19,54% и выпуск продукции машиностроения на 30,52% по сравнению с исходными величинами, указанными в таблице.

Ответ:

1) матрица А прямых затрат:

;

2) матрица полных затрат:

;

3. если конечное потребление увеличить по отраслям соответственно на 30, 10 и 50%, то прирост объемов валовых выпусков по каждой отрасли составит соответственно 26,26; 19,54; 30,52%.