
- •Содержание
- •Лекция 1. Матрицы и определители n-го порядка.
- •1.1. Матрицы, их виды, линейные операции над матрицами
- •1.2. Умножение матриц
- •1.3 Определителиn-го порядка и их свойства
- •1.4. Обратная матрица
- •Лекция 2. Системы линейных уравнений и их решение
- •2.1. Системыmлинейных уравнений сnнеизвестными. Основные понятия
- •2.2. Решение системnлинейных уравнений сnнеизвестными по формулам Крамера
- •2.3. Решение системnлинейных уравнений сnнеизвестными матричным способом
- •2.4. Решение системmлинейных уравнений сnнеизвестными методом Гаусса
- •2.5. Ранг матрицы. Теорема Кронекера-Капелли
- •2.6. Однородные системы
- •Лекция 3. Решение матричных уравнений
- •Замечания.
- •1) При решении необходимо определить тип матричного уравнения и метод его решения.
- •3.2. Собственные векторы и собственные значения матрицы
- •3.3. Модель Леонтьева многоотраслевой экономики
- •Лекция 4. Векторы на плоскости и в пространстве
- •4.1. Векторы и линейные операции над ними
- •1) ; 2)Если;
- •3) Если; 4)
- •4.2. Проекция вектора на ось
- •4.3. Скалярное произведение векторов
- •4.4. Векторное произведение векторов
- •4.5 Смешанное произведение векторов
- •Лекция 5. Координатный метод
- •5.1. Системы координат на плоскости
- •5.2.Системы координат в пространстве
- •Лекция 6. Уравнения прямой и плоскости в пространстве
- •6.1. Плоскость в пространстве
- •6.2. Прямая в пространстве
- •6.3. Взаимное расположение прямой и плоскости в пространстве
- •Лекция 7. Прямая линия на плоскости
- •7.1. Уравнения прямой на плоскости
- •7.2. Взаимное расположение прямых на плоскости
- •Лекция 8. Линии второго порядка и поверхности второго порядка
- •8.1. Кривые второго порядка. Основные понятия
- •8.2. Поверхности второго порядка
- •Лекция 9. Теоретико-множественные понятия в математике
- •9.1. Понятие множества. Круги Эйлера. Операции над множествами
- •9.2. Отношения и отображения как соответствия между элементами множеств. Мощность множества
- •9.3. Множество действительных чиселRи его основные подмножества
- •9.4. Окрестность точки, элементы топологии
- •Лекция 10. Действительные и комплексные числа
- •10.1. Действительные числа и их основные свойства
- •10.2. Определение комплексных чисел, комплексная плоскость, формы записи комплексных чисел
- •10.3. Операции с комплексными числами
- •Лекция 11. Многочлены
- •11.1. Многочлены. Разложение многочленов на множители
- •11.2. Рациональные дроби: правильные и неправильные. Простейшие рациональные дроби
- •11.3. Разложение правильной алгебраической дроби на сумму простейших
- •Лекция 12. Линейные пространства
- •12.1. Определение линейного пространства, свойства линейных пространств. Примеры линейных пространств
- •12.2. Подпространство линейного пространства
- •12.3. Линейно зависимые и независимые векторы. Базис и размерность линейных пространств
- •12.4. Евклидово пространство. Ортогональная система векторов. Процесс ортогонализации
- •Лекция 13. Линейные операторы
- •13.1. Определение линейного оператора и его основные свойства. Линейное пространство операторов, действующих из х в у
- •13.2. Свойства линейных операторов, действующих из х в х. Определение обратного оператора. Условие обратимости линейного оператора
- •13.3. Матрица линейного оператора
- •13.4. Переход к новому базису. Матрица перехода и её основные свойства. Связь координат вектора и матриц линейного оператора при переходе к новому базису
- •13.5. Собственные векторы и собственные значения линейного преобразования
- •13.6. Линейная модель обмена
- •Лекция 14. Квадратичные формы
- •14.2. Поведение квадратичной формы при линейном преобразовании переменных
- •14.3. Приведение квадратичной формы к каноническому виду
- •14.4. Свойства канонических форм. Знакоопределенность
- •Лекция 15. Математические структуры
- •15.1. Понятие структуры
- •15.2. Алгебраические структуры: группы и полугруппы, подгруппы, кольца и поля
- •15.3. Матричные алгебраические структуры
- •Рекомендуемая литература
9.4. Окрестность точки, элементы топологии
Пусть
𝜺
– произвольное положительное число,
𝜺

Определение 1. 𝜺 – окрестностью точки x0 Є R называется интервал
(x0 –𝜺, x0 + 𝜺) или х: |x - x0| < 𝜺.
(
.
) 
x0 – 𝜺 x0 x0 + 𝜺
Пусть X – произвольное множество, &= { Ui, i Є I } – некоторое семейство его подмножеств, где множество I имеет произвольную мощность.
Определение 2. Семейство & определяет во множестве Х топологию, если
1) X и Ø Є U;
2) объединение любого числа множеств из семейства & принадлежит
семейству &;
3) Пересечение конечного числа множеств из семейства & принадлежит &.
Примеры топологических пространств (X, U) :
Х = R, & – семейство окрестностей. Понятия точки прикосновения, предельной точки, сходимости последовательности точек, непрерывности функций могут быть описаны в терминах открытых множеств (в терминах окрестностей точек).
Лекция 10. Действительные и комплексные числа
10.1. Действительные числа и их основные свойства
10.2. Определение комплексных чисел, комплексная плоскость, формы записи комплексных чисел
10.3. Операции с комплексными числами
10.1. Действительные числа и их основные свойства
Множество действительных чисел состоит из двух множеств: рациональных и иррациональных чисел.
Рациональным
называется число, которое может быть
представлено в виде несократимой дроби
вида
 ,
гдеm
и n
,
гдеm
и n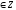 ,
,
 .
.
Иррациональными
числами являются бесконечные,
непериодические, единственным образом
определены два действительных числа a
+ b
и a
 b,
называемые суммой и произведением и
обладающие следующими свойствами:
b,
называемые суммой и произведением и
обладающие следующими свойствами:
1.

2.
(a
+ b)+ =a
+( b
+
=a
+( b
+ );
);
 ;
;
3.
 .
.
4. «0» - нейтральное число относительно суммы: a +0 = a.
5.
«1» - нейтральное число относительно
произведения:

6. Существует элемент «-a»: a +(- a) = 0.
7.
Существует элемент «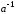 »:
»: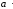
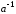 = 1.
= 1.
Все
действительные числа обладают свойством
непрерывности, то есть если для любых
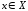 и
и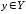 выполняется
неравенство
выполняется
неравенство ,
то существует хотя бы одно число
,
то существует хотя бы одно число :
:
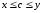 .
.
Для
любых двух различных действительных
чисел установлено одно из отношений: a
= b;
a
> b;
a
< b,
причём если a
> b
и
 >0,
то
>0,
то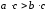 .
И еслиa
> b,
то a
+
.
И еслиa
> b,
то a
+ >
b
+
>
b
+ .
.
Из перечисленных свойств вытекают все остальные свойства действительных чисел. Поэтому можно считать, что множество элементов, обладающих перечисленными свойствами, называется множеством действительных чисел, причём предложенное определение множества действительных чисел называется аксиоматическим.
10.2. Определение комплексных чисел, комплексная плоскость, формы записи комплексных чисел
Определение.
Выражение вида
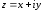 называется комплексным числом.
называется комплексным числом.
Элемент
 =
=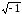 называется «мнимой единицей». Элементы
называется «мнимой единицей». Элементы и
и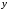 - любые действительные числа. Число
- любые действительные числа. Число называется действительной частью
комплексного числа и обозначается
называется действительной частью
комплексного числа и обозначается .
Число
.
Число называется мнимой частью комплексного
числа и обозначается
называется мнимой частью комплексного
числа и обозначается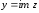 .
Запись комплексного числа, представленного
выше, называется алгебраической записью
комплексного числа.
.
Запись комплексного числа, представленного
выше, называется алгебраической записью
комплексного числа.
Модулем
комплексного числа
 называется число
называется число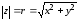 .
.
Каждому
комплексному числу соответствует пара
действительных чисел ( ;
; )
и наоборот. Поэтому комплексные числа
удобно интерпретировать геометрически
как точки на плоскости. Плоскость,
содержащая комплексные числа называется
комплексной и обозначается
)
и наоборот. Поэтому комплексные числа
удобно интерпретировать геометрически
как точки на плоскости. Плоскость,
содержащая комплексные числа называется
комплексной и обозначается .
В ней осьox
- действительная, а ось oy
- мнимая.
.
В ней осьox
- действительная, а ось oy
- мнимая.
Определение
Угол
 ,
образованный радиус-вектором
,
образованный радиус-вектором с
положительным направлением оси
с
положительным направлением оси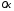 называется аргументом комплексного
числа и обозначается:Arg
называется аргументом комплексного
числа и обозначается:Arg .
.

Наименьшее
по модулю значение аргумента называется
главным аргументом и обозначается:
arg ,
,
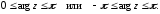 Аргумент комплексного числа определяется
неоднозначно, а с точностью до слагаемого
кратного
Аргумент комплексного числа определяется
неоднозначно, а с точностью до слагаемого
кратного :Arg
:Arg =
arg
=
arg +2к
+2к .
.
Если
учесть, что
 ,
а
,
а ,
то
,
то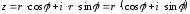 - тригонометрическая форма комплексного
числа, где
- тригонометрическая форма комплексного
числа, где ,
а
,
а
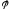 -аргумент
комплексного числа.
-аргумент
комплексного числа.
 -
показательная форма записи комплексного
числа, при этом
-
показательная форма записи комплексного
числа, при этом
 =
= (формула Эйлера).
(формула Эйлера).
