67. 12.2. Подпространство линейного пространства

Определение. Множество L называется подпространством линейного пространства Е, если выполняются следующие условия:

1. Любой элемент х Є L является элементом множества Е,

2. Для любых х и у множества L элемент х + у Є L ,

3. Для любого х Є L и для любого действительного λ элемент λ х Є L .

Из определения следует, что линейное подпространство само является линейным пространством.

Примеры линейных подпространств

1. В линейном пространстве Е свободных векторов трехмерного пространства R³ линейное подпространство образуют:

а) все векторы, параллельные заданной плоскости ;

b) все векторы, параллельные данной прямой.

2. В линейном пространстве квадратных матриц порядка линейное подпространство образуют:

а) все симметричные матрицы;

б) все верхние ( нижние ) треугольные матрицы.

3. Пусть Е - линейное пространство, и х₁, х₂, х₃, … , х_n Є Е, тогда множество всех линейных комбинаций этих элементов вида α₁ х₁ + α₂ х₂ + α₃ х₃ + … + α_n x_n , где α₁ , α₂, α₃ ,… , α_n – действительные числа, является векторным подпространством пространства Е.

68. 12.3. Линейно зависимые и независимые векторы. Базис и размерность линейных пространств

Пусть Е = { x, y, z, t, … } - линейное пространство, его элементы x, y, z, t, … будем называть векторами.

Рассмотрим векторы х₁, х₂, х₃, … , х_i , … , х_n Є Е

и действительные числа α₁ , α₂ , α₃ , … , α_i , … , α_n.

Определение 1. Линейной комбинацией векторов х₁, х₂, х₃, … , х_i , … , х_n Є Е называется вектор

α₁ х₁ + α₂ х₂ + α₃ х₃ + … + α _i x _i + … + α_n x _n = 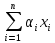Є E .

Определение 2. Векторы х₁, х₂, х₃, … , х_i , … , х_n Є Е называются линейно зависимыми, если равенство нулю их линейной комбинации α₁ х₁ + α₂ х₂ + α₃ х₃ + … + α _i x _i + … + α_n x _n = 0 (1) возможно хотя бы при одном из коэффициентов α₁, α₂, α₃, …, α_i , …, α_n отличном от нуля.

Определение 3. Векторы х₁, х₂, х₃, … , х_i , … , х_n Є Е называются линейно независимыми, если равенство нулю их линейной комбинации α₁ х₁ + α₂ х₂ + α₃ х₃ + … + α _i x _i + … + α_n x _n = 0 возможно тогда и только тогда, когда все коэффициенты линейной комбинации α₁ , α₂ , α₃ , … , α_i, … , α_n равны нулю.

Можно показать, что если векторы х₁, х₂, х₃, … , х_i , … , х_n Є Е линейно зависимы, то по крайней мере один из них линейно выражается через остальные. Верно и обратное утверждение о том, что если один из векторов выражается линейно через остальные, то все эти векторы в совокупности линейно зависимы.

Примеры

1.Любые два непараллельных вектора на плоскости линейно независимы. Однако любые три вектора на плоскости линейно зависимы.

2.Единичные векторы 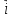=,,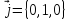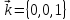линейно независимы вR³.

3. Функции х₁ = , х₂ =( 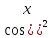, х₃ = 1 линейно зависимы, так как α₁ х₁ + α₂ х₂ + α₃ х₃ = α₁ + α₂ ( + α₃ * 1 = 0 при α₁ = 1, α₂ = 1, α₃ = - 1.

Отметим некоторые свойства системы векторов линейного пространства.

1. Если среди векторов х₁, х₂, х₃, … , х_i , … , х_n Є Е имеется нулевой вектор, то эти векторы линейно зависимы. В самом деле, если, например, х₁ = 0 , то равенство (1) справедливо при α₁ = 1, α₂ = α₃ = … = α_i = … = α_n = 0 .

2. Если система векторов х₁, х₂, х₃, … , х_i , … , х_n Є Е содержит линейно зависимую подсистему, то такая система векторов линейно зависима.

Определение 4. Базисом линейного пространства Е называется совокупность линейно независимых векторов е₁, е₂, е₃, …, е_i , …, е_n Є Е , если для любого элемента х Є Е существуют действительные числа α₁, α₂ , α₃ , … , α_i, … , α_n такие, что

х = α₁ е₁ + α₂ е₂ + α₃ е₃ + … + α _i е_i + … + α_n е _n (2)

Действительные числа α₁ , α₂ , α₃ , … , α_i, … , α_n называются координатами вектора х в базисе е₁, е₂, е₃, … , е_i , … , е_n .

Теорема 1. Каждый вектор х линейного пространства Е можно представить и притом единственным образом в виде линейной комбинации базисных векторов.

Определение 5. Линейное пространство Е называется n - мерным, если в нем существует n линейно независимых векторов, и любые n + 1 векторов этого пространства линейно зависимы.

Определение 6. Размерностью линейного пространства называется максимальное число линейно независимых векторов этого пространства.

Теорема 2. Если размерность линейного пространства Е равна n , то любые n линейно независимых векторов являются базисом этого пространства.

Теорема 3. Если базис линейного пространства Е состоит из n линейно независимых векторов, то размерность линейного пространства равна n.

Замечание. Линейное пространство Е называется бесконечномерным, если в нем существует любое конечное число линейно независимых векторов.