
- •Содержание
- •Лекция 1. Матрицы и определители n-го порядка.
- •1.1. Матрицы, их виды, линейные операции над матрицами
- •1.2. Умножение матриц
- •1.3 Определителиn-го порядка и их свойства
- •1.4. Обратная матрица
- •Лекция 2. Системы линейных уравнений и их решение
- •2.1. Системыmлинейных уравнений сnнеизвестными. Основные понятия
- •2.2. Решение системnлинейных уравнений сnнеизвестными по формулам Крамера
- •2.3. Решение системnлинейных уравнений сnнеизвестными матричным способом
- •2.4. Решение системmлинейных уравнений сnнеизвестными методом Гаусса
- •2.5. Ранг матрицы. Теорема Кронекера-Капелли
- •2.6. Однородные системы
- •Лекция 3. Решение матричных уравнений
- •Замечания.
- •1) При решении необходимо определить тип матричного уравнения и метод его решения.
- •3.2. Собственные векторы и собственные значения матрицы
- •3.3. Модель Леонтьева многоотраслевой экономики
- •Лекция 4. Векторы на плоскости и в пространстве
- •4.1. Векторы и линейные операции над ними
- •1) ; 2)Если;
- •3) Если; 4)
- •4.2. Проекция вектора на ось
- •4.3. Скалярное произведение векторов
- •4.4. Векторное произведение векторов
- •4.5 Смешанное произведение векторов
- •Лекция 5. Координатный метод
- •5.1. Системы координат на плоскости
- •5.2.Системы координат в пространстве
- •Лекция 6. Уравнения прямой и плоскости в пространстве
- •6.1. Плоскость в пространстве
- •6.2. Прямая в пространстве
- •6.3. Взаимное расположение прямой и плоскости в пространстве
- •Лекция 7. Прямая линия на плоскости
- •7.1. Уравнения прямой на плоскости
- •7.2. Взаимное расположение прямых на плоскости
- •Лекция 8. Линии второго порядка и поверхности второго порядка
- •8.1. Кривые второго порядка. Основные понятия
- •8.2. Поверхности второго порядка
- •Лекция 9. Теоретико-множественные понятия в математике
- •9.1. Понятие множества. Круги Эйлера. Операции над множествами
- •9.2. Отношения и отображения как соответствия между элементами множеств. Мощность множества
- •9.3. Множество действительных чиселRи его основные подмножества
- •9.4. Окрестность точки, элементы топологии
- •Лекция 10. Действительные и комплексные числа
- •10.1. Действительные числа и их основные свойства
- •10.2. Определение комплексных чисел, комплексная плоскость, формы записи комплексных чисел
- •10.3. Операции с комплексными числами
- •Лекция 11. Многочлены
- •11.1. Многочлены. Разложение многочленов на множители
- •11.2. Рациональные дроби: правильные и неправильные. Простейшие рациональные дроби
- •11.3. Разложение правильной алгебраической дроби на сумму простейших
- •Лекция 12. Линейные пространства
- •12.1. Определение линейного пространства, свойства линейных пространств. Примеры линейных пространств
- •12.2. Подпространство линейного пространства
- •12.3. Линейно зависимые и независимые векторы. Базис и размерность линейных пространств
- •12.4. Евклидово пространство. Ортогональная система векторов. Процесс ортогонализации
- •Лекция 13. Линейные операторы
- •13.1. Определение линейного оператора и его основные свойства. Линейное пространство операторов, действующих из х в у
- •13.2. Свойства линейных операторов, действующих из х в х. Определение обратного оператора. Условие обратимости линейного оператора
- •13.3. Матрица линейного оператора
- •13.4. Переход к новому базису. Матрица перехода и её основные свойства. Связь координат вектора и матриц линейного оператора при переходе к новому базису
- •13.5. Собственные векторы и собственные значения линейного преобразования
- •13.6. Линейная модель обмена
- •Лекция 14. Квадратичные формы
- •14.2. Поведение квадратичной формы при линейном преобразовании переменных
- •14.3. Приведение квадратичной формы к каноническому виду
- •14.4. Свойства канонических форм. Знакоопределенность
- •Лекция 15. Математические структуры
- •15.1. Понятие структуры
- •15.2. Алгебраические структуры: группы и полугруппы, подгруппы, кольца и поля
- •15.3. Матричные алгебраические структуры
- •Рекомендуемая литература
Лекция 1. Матрицы и определители n-го порядка.
1.1. Матрицы, их виды, линейные операции над матрицами
1.2. Умножение матриц
1.3. Определители n-го порядка и их основные свойства
1.4. Обратная матрица
1.1. Матрицы, их виды, линейные операции над матрицами
Определение. Матрицей называется прямоугольная таблица, содержащая m строк и n столбцов.
Числа m и n определяют размер матрицы, который записывается m x n. Для сокращения записи матрицы используются заглавные буквы.
Пример:

Решение
В
общем виде записывается:
 илиA
= (aij),
где числа aij
– элементы матрицы, причём
илиA
= (aij),
где числа aij
– элементы матрицы, причём
 и
и - индексы строки и столбца соответственно.
- индексы строки и столбца соответственно.
Виды матриц
1.
Прямоугольная матрица, если
 .
.
2.
Квадратная матрица, если
 .
Числоn
называется
порядком квадратной матрицы.
.
Числоn
называется
порядком квадратной матрицы.
3. Матрица размера 1x n называется матрицей-строкой.
4. Матрица размера m x1 называется матрицей-столбцом.
5.
Квадратная матрица, у которой элементы
с разными индексами равны 0 (aij
= 0 при
 ),
а с одинаковыми индексами равны 1 (aij
= 1 при i
= j),
называется единичной матрицей и
обозначается E.
),
а с одинаковыми индексами равны 1 (aij
= 1 при i
= j),
называется единичной матрицей и
обозначается E.
6. Матрица, все элементы которой равны нулю, называется нулевой матрицей.
7. Матрицы называются равными, если они имеют одинаковые размеры и их соответствующие элементы равны.
8.
Диагональной матрицей называется
квадратная матрица, у которой элементы
с разными индексами aij
= 0 при
 .
.
9.
Скалярной матрицей называется диагональная
матрица, у которой диагональные элементы
 равны одному и тому же числу.
равны одному и тому же числу.
Линейные операции над матрицами
1.
Суммой матриц A
и B
называется матрица C,
каждый элемент которой представляет
собой сумму соответствующих элементов
матриц A
и B,
то есть

Например:

Складываются матрицы одного размера!
2.
При умножении матрицы на число каждый
элемент матрицы умножается на это число,
то есть

Например:

Свойства операции сложения матриц
А+В=В+А
(А+В)+С=А+(В+С)
k(А+В)=kА+kВ
Если строки матрицы А поменять местами со столбцами, причём каждую строку заменить столбцом с тем же номером, то полученная матрица называется транспонированной к матрице А и обозначается AT, то есть для матрицы

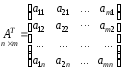
транспонированная матрица. Операция перехода от A к AT называется транспонированием.
1.2. Умножение матриц
Определение.
Произведением матрицы A
= (aij)
размера mxn
( ,
, )
на матрицуB
= (bjk)
размера nxp
(
)
на матрицуB
= (bjk)
размера nxp
( ,
, )
называется матрица
)
называется матрица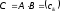 размераmxp,
каждый элемент
размераmxp,
каждый элемент
 которой равен сумме попарных произведений
элементовi-ой
строки матрицы A
на соответствующие им элементы k-го
столбца матрицы B,
то есть
которой равен сумме попарных произведений
элементовi-ой
строки матрицы A
на соответствующие им элементы k-го
столбца матрицы B,
то есть
 .
.
!!! Перемножаются только такие две матрицы, у которых число столбцов первой равно числу строк второй.
Например:
Пример:
1. ;
;
2. ;
;
3.
 =
= —
не существует, так как число столбцов
матрицыA
равно 2, а число строк матрицы
B
равна 3.
—
не существует, так как число столбцов
матрицыA
равно 2, а число строк матрицы
B
равна 3.
Замечания
1.
а) Если произведение матриц
 существует, то произведение матриц
существует, то произведение матриц может и не существовать. Например
может и не существовать. Например существует, а
существует, а
 не существует, так
как число столбцов первой матрицы не
совпадает с числом строк второй матрицы;
не существует, так
как число столбцов первой матрицы не
совпадает с числом строк второй матрицы;
б)
если оба произведения
 и
и существуют, то они могут быть матрицами
разных размеров, например
существуют, то они могут быть матрицами
разных размеров, например ,а
,а  ,то есть
,то есть
 ;
;
в)
если А
и В
– квадратные матрицы одного и того же
порядка, то оба произведения
 и
и существуют, но
переместительный закон умножения ,
вообще говоря, не выполняется, то есть
существуют, но
переместительный закон умножения ,
вообще говоря, не выполняется, то есть
 ;
;
2.
Умножение матриц не обладает перестановочным
свойством, вообще говоря
 .
.
3.
Если ,
то такие матрицы называются перестановочными
или коммутативными.
,
то такие матрицы называются перестановочными
или коммутативными.
Свойства операции транспонирования
1.

2.

3.

4.

Свойства операции умножения матриц
1.
 ;
;
2.
 ;
;
3.
 ;
;
4.
 гдеE
– единичная матрица, A
– квадратная матрица того же порядка
что и E.
гдеE
– единичная матрица, A
– квадратная матрица того же порядка
что и E.
5.
 ,где D
- скалярная
матрица, А
– квадратная матрица того же порядка
что и D.
,где D
- скалярная
матрица, А
– квадратная матрица того же порядка
что и D.
