
- •Содержание
- •Лекция 1. Матрицы и определители n-го порядка.
- •1.1. Матрицы, их виды, линейные операции над матрицами
- •1.2. Умножение матриц
- •1.3 Определителиn-го порядка и их свойства
- •1.4. Обратная матрица
- •Лекция 2. Системы линейных уравнений и их решение
- •2.1. Системыmлинейных уравнений сnнеизвестными. Основные понятия
- •2.2. Решение системnлинейных уравнений сnнеизвестными по формулам Крамера
- •2.3. Решение системnлинейных уравнений сnнеизвестными матричным способом
- •2.4. Решение системmлинейных уравнений сnнеизвестными методом Гаусса
- •2.5. Ранг матрицы. Теорема Кронекера-Капелли
- •2.6. Однородные системы
- •Лекция 3. Решение матричных уравнений
- •Замечания.
- •1) При решении необходимо определить тип матричного уравнения и метод его решения.
- •3.2. Собственные векторы и собственные значения матрицы
- •3.3. Модель Леонтьева многоотраслевой экономики
- •Лекция 4. Векторы на плоскости и в пространстве
- •4.1. Векторы и линейные операции над ними
- •1) ; 2)Если;
- •3) Если; 4)
- •4.2. Проекция вектора на ось
- •4.3. Скалярное произведение векторов
- •4.4. Векторное произведение векторов
- •4.5 Смешанное произведение векторов
- •Лекция 5. Координатный метод
- •5.1. Системы координат на плоскости
- •5.2.Системы координат в пространстве
- •Лекция 6. Уравнения прямой и плоскости в пространстве
- •6.1. Плоскость в пространстве
- •6.2. Прямая в пространстве
- •6.3. Взаимное расположение прямой и плоскости в пространстве
- •Лекция 7. Прямая линия на плоскости
- •7.1. Уравнения прямой на плоскости
- •7.2. Взаимное расположение прямых на плоскости
- •Лекция 8. Линии второго порядка и поверхности второго порядка
- •8.1. Кривые второго порядка. Основные понятия
- •8.2. Поверхности второго порядка
- •Лекция 9. Теоретико-множественные понятия в математике
- •9.1. Понятие множества. Круги Эйлера. Операции над множествами
- •9.2. Отношения и отображения как соответствия между элементами множеств. Мощность множества
- •9.3. Множество действительных чиселRи его основные подмножества
- •9.4. Окрестность точки, элементы топологии
- •Лекция 10. Действительные и комплексные числа
- •10.1. Действительные числа и их основные свойства
- •10.2. Определение комплексных чисел, комплексная плоскость, формы записи комплексных чисел
- •10.3. Операции с комплексными числами
- •Лекция 11. Многочлены
- •11.1. Многочлены. Разложение многочленов на множители
- •11.2. Рациональные дроби: правильные и неправильные. Простейшие рациональные дроби
- •11.3. Разложение правильной алгебраической дроби на сумму простейших
- •Лекция 12. Линейные пространства
- •12.1. Определение линейного пространства, свойства линейных пространств. Примеры линейных пространств
- •12.2. Подпространство линейного пространства
- •12.3. Линейно зависимые и независимые векторы. Базис и размерность линейных пространств
- •12.4. Евклидово пространство. Ортогональная система векторов. Процесс ортогонализации
- •Лекция 13. Линейные операторы
- •13.1. Определение линейного оператора и его основные свойства. Линейное пространство операторов, действующих из х в у
- •13.2. Свойства линейных операторов, действующих из х в х. Определение обратного оператора. Условие обратимости линейного оператора
- •13.3. Матрица линейного оператора
- •13.4. Переход к новому базису. Матрица перехода и её основные свойства. Связь координат вектора и матриц линейного оператора при переходе к новому базису
- •13.5. Собственные векторы и собственные значения линейного преобразования
- •13.6. Линейная модель обмена
- •Лекция 14. Квадратичные формы
- •14.2. Поведение квадратичной формы при линейном преобразовании переменных
- •14.3. Приведение квадратичной формы к каноническому виду
- •14.4. Свойства канонических форм. Знакоопределенность
- •Лекция 15. Математические структуры
- •15.1. Понятие структуры
- •15.2. Алгебраические структуры: группы и полугруппы, подгруппы, кольца и поля
- •15.3. Матричные алгебраические структуры
- •Рекомендуемая литература
8.2. Поверхности второго порядка
Определение. Поверхность R3, которая в декартовой системе координат определяется уравнением второй степени, называется поверхностью второго порядка.
Общее уравнение поверхности 2-го порядка имеет вид:
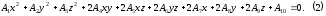
Это уравнение может определять сферу, эллипсоид, однополостной или двуполостной гиперболоид, эллиптический или гиперболический параболоид, цилиндрическую или коническую поверхности второго порядка. Оно может также определять совокупность двух плоскостей, точку, прямую или даже не иметь геометрического смысла. Если уравнение (2) определяет поверхность, среди сечений плоскостями которой имеются какие-либо кривые из линий второго порядка: окружность, гипербола, эллипс, парабола, то с помощью переноса начала координат и поворота осей координат уравнение (2) приобретает вид канонического уравнения соответствующей поверхности второго порядка. Приведем некоторые примеры:
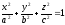 –эллипсоид;
–эллипсоид;
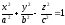 –однополостной
гиперболоид;
–однополостной
гиперболоид;
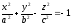 –двуполостной
гиперболоид;
–двуполостной
гиперболоид;
 –конус;
–конус;
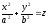 –эллиптический
параболоид;
–эллиптический
параболоид;
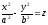 –гиперболический
параболоид;
–гиперболический
параболоид;
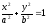 –эллиптический
цилиндр;
–эллиптический
цилиндр;
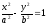 –гиперболический
цилиндр;
–гиперболический
цилиндр;
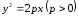 –параболический
цилиндр.
–параболический
цилиндр.
Если
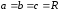 ,
то эллипсоид обращается в сферу. Если
лежащая в координатной плоскости кривая
вращается вокруг какой-либо координатной
оси, то образуется поверхность, называемая
поверхностью вращения.
,
то эллипсоид обращается в сферу. Если
лежащая в координатной плоскости кривая
вращается вокруг какой-либо координатной
оси, то образуется поверхность, называемая
поверхностью вращения.
Например,
если у эллипса a
= b,
то, вращая его вокруг оси оz,
получим поверхность вращения - эллипсоид
вращения, имеющий уравнение
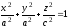 ,где
,где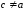 .
.
Лекция 9. Теоретико-множественные понятия в математике
9.1. Понятие множества. Круги Эйлера. Операции над множествами
9.2. Отношения и отображения как соответствия между элементами множеств. Мощность множества
9.3. Множество действительных чисел и его основные подмножества
9.4. Окрестность точки, элементы топологии
9.1. Понятие множества. Круги Эйлера. Операции над множествами
Множество – совокупность, набор каких-либо предметов (объектов) произвольной природы, объединенных по какому –либо общему для них признаку (множество студентов данной группы, множество цветных телевизоров в гостинице, множество чисел первого десятка, множество точек на прямой и т. д.).Немецкий математик Г.Кантор считал, что «множество есть многое, мыслимое нами как единое». Понятие множества, точки, числа приходится принимать без определения.
Объекты,
из которых состоит множество, называют
его элементами.
Если элементами множества являются
числа, то оно называется числовым
множеством.
Множества
обозначаются большими буквами латинского
алфавита А, В, С,…, а их элементы- малыми
буквами этого алфавита. Если элемент х
принадлежит множеству А, то пишут х А,
если же х не принадлежит множеству А,
то пишут х
А,
если же х не принадлежит множеству А,
то пишут х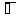 А.
А.
Множества можно задать двумя способами:
перечислить его элементы;
описать его элементы с помощью характеристического свойства.
Множество, не имеющее элементов, называют пустым и обозначают Ø.
Примеры пустых множеств:
Множество действительных чисел, являющихся корнями уравнения
х2 +1=0.
2) Множество треугольников, сумма углов которых ≠ 180.
3) Множество решений системы уравнений
3х
+4у =7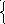
6х +8у = 10
Множества бывают конечными и бесконечными. Например, множество А= { 0,1,2,3,4,5,6,7,8,9 } всех цифр - конечное, а множество всех целых чисел, составленных из этих цифр - бесконечное.
Одно и то же множество может быть задано разными характеристическими свойствами: множество А ={ 2,4 } можно определить как множество четных чисел, удовлетворяющих неравенству А = { х: 1 < x < 5, х- четное} и как множество корней квадратного уравнения х2 – 6 х + 8 = 0: А = { х: х2 – 6 х + 8 = 0 }
Примеры множеств в геометрии, описываемых
характеристическими свойствами:
биссектриса угла – геометрическое место точек плоскости, лежащих
внутри угла и равноудаленных от его сторон;
окружность- геометрическое место точек плоскости, равноудаленных от фиксированной точки – центра окружности.
Множество, содержащее все те элементы, которые встречаются в контексте проводимых рассуждений, называется универсальным и обозначается Е.
Два
множества А и В считаются равными, если
они состоят из одних и тех же элементов:
А = В ↔ для любого х ( х
 А ↔ х
А ↔ х В).
В).
Множество А называется подмножеством множества В : А С В , если
из
того, что х
 А следует, что х
А следует, что х В.
В.
Если А С В и В С А, то множества А и В равны : А=В.
Для обозначения множеств удобно использовать круги Эйлера, диаграммы Венна, диаграммы Эйлера – Венна – это замкнутые линии, внутри которых расположены элементы данного множества, а снаружи – элементы, не принадлежащие множеству.
В
В
А
А С В
Пусть Е – какое-либо множество, рассмотрим всевозможные его подмножества. В этом случае Е является универсальным множеством.
1) Пусть Е – какое-либо множество книг, его подмножества: научные книги, художественные книги, книги по искусству, учебники.
2) Е = { а, в, с } и его подмножества: { Ø, { а,в,с }, {а}, {в}, {с}, {а,в}, {в,с}, {а,с} }, количество таких подмножеств 23 = 8.
Если Е – универсальное множество, состоящее из n элементов, то число его подмножеств 2n.
Операции над множествами
1)
Объединением(
или суммой
) множеств
А и В называется множество
С = А
 В , составленное из всех элементов,
принадлежащих хотя бы одному из этих
множеств, т.е. из элементов, входящих
либо в А, либо в В (не исключается
возможность одновременной принадлежности
и к множеству А и к множеству В). Знак
В , составленное из всех элементов,
принадлежащих хотя бы одному из этих
множеств, т.е. из элементов, входящих
либо в А, либо в В (не исключается
возможность одновременной принадлежности
и к множеству А и к множеству В). Знак называется знаком объединения.
называется знаком объединения.
А
В
А
В
С
А
 В А
В А B
B
 C
C
2) Пересечением (или произведением) множеств А и В называется множество С = А ∩ В, состоящее из элементов, принадлежащих и множеству А, и множеству В одновременно. Знак ∩ называется знаком пересечения.
А
А
В
В
А
В
С
А ∩ В А ∩ В ∩ С А ∩ В=А
3) Разностью множеств А и В называется множество С = А \ В, состоящее из элементов множества А, не входящих во множество В.
А
А
В
А
B
В
А \ В А\ В А\ В=А
Результат применения операций к множествам изображается на кругах Эйлера.
Пусть Е – универсальное множество, А С Е.
Множество Ā = Е \ А называется дополнением до множества А.
а) Е – множество студентов в группе, А – юноши, Ā – девушки.
б) Е – множество прямоугольников, А – множество квадратов, Ā – множество прямоугольников с разными (неравными) сторонами.
в) Е – множество целых чисел, А = {множество четных чисел}, Ā = { множество нечетных чисел }.
Пример: пусть А – множество натуральных делителей числа 72, а В – множество натуральных делителей числа 54:
А = { 1; 2; 3; 4; 6, 8, 9, 12, 18, 24, 36, 72}, В = {1, 2, 3, 6, 9, 18, 27, 54}.
Тогда: А U В = {1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72 },
А ∩ В = {1, 2, 3, 6, 9, 18 }, А \ В = { 8, 4, 12, 24, 36, 72}.
4) Декартовым произведением множеств А и В называется множество
А х В всех упорядоченных пар элементов (а, b), где а Є А, b Є В.
Если множество А = {1,2 }, а множество В = {1, 2, 3}, тогда
А х В = { (1, 2), (1, 1), (1 ,3), (2, 1), (2, 2), (2, 3)},
В х А = { (1, 1), (1, 2), (2, 1), (2, 2), (3, 1), (3, 2)}
В
В
АхВ
ВхА












А
А
Основные законы операций над множествами
1)
А
 В = В
В = В А, А ∩ В = В ∩ А (переместительный),
А, А ∩ В = В ∩ А (переместительный),
2)
(А
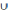 B)
B)
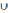 C
= A
C
= A
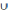 (B
(B
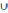 C)
, (А ∩ В) ∩ C=
A
∩ (B∩C)
(сочетательный),
C)
, (А ∩ В) ∩ C=
A
∩ (B∩C)
(сочетательный),
3)
А
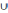 Ø = А, А ∩ Ø = Ø, Ø \ А = Ø, А \ А = Ø, Ø
играет роль нуля в алгебре, но Ø \ А = Ø
не имеет аналога в алгебре.
Ø = А, А ∩ Ø = Ø, Ø \ А = Ø, А \ А = Ø, Ø
играет роль нуля в алгебре, но Ø \ А = Ø
не имеет аналога в алгебре.
4)
Ẫ = А,
А
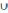 Ā = E, A ∩ Ā = Ø, E \ A = Ā, A \ E = Ø,А
Ā = E, A ∩ Ā = Ø, E \ A = Ā, A \ E = Ø,А
 A = A,
A = A,
A
∩ A = A, A
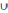 E = E, A ∩ E = A.
E = E, A ∩ E = A.
5)
А
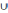 (B ∩ C) = (A
(B ∩ C) = (A B) ∩ (A
B) ∩ (A C)
C)
Законы Моргана
A
∩ (B
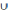 C) = (A ∩ B)
C) = (A ∩ B)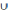 (A ∩ C)
(A ∩ C)
