
- •Содержание
- •Лекция 1. Матрицы и определители n-го порядка.
- •1.1. Матрицы, их виды, линейные операции над матрицами
- •1.2. Умножение матриц
- •1.3 Определителиn-го порядка и их свойства
- •1.4. Обратная матрица
- •Лекция 2. Системы линейных уравнений и их решение
- •2.1. Системыmлинейных уравнений сnнеизвестными. Основные понятия
- •2.2. Решение системnлинейных уравнений сnнеизвестными по формулам Крамера
- •2.3. Решение системnлинейных уравнений сnнеизвестными матричным способом
- •2.4. Решение системmлинейных уравнений сnнеизвестными методом Гаусса
- •2.5. Ранг матрицы. Теорема Кронекера-Капелли
- •2.6. Однородные системы
- •Лекция 3. Решение матричных уравнений
- •Замечания.
- •1) При решении необходимо определить тип матричного уравнения и метод его решения.
- •3.2. Собственные векторы и собственные значения матрицы
- •3.3. Модель Леонтьева многоотраслевой экономики
- •Лекция 4. Векторы на плоскости и в пространстве
- •4.1. Векторы и линейные операции над ними
- •1) ; 2)Если;
- •3) Если; 4)
- •4.2. Проекция вектора на ось
- •4.3. Скалярное произведение векторов
- •4.4. Векторное произведение векторов
- •4.5 Смешанное произведение векторов
- •Лекция 5. Координатный метод
- •5.1. Системы координат на плоскости
- •5.2.Системы координат в пространстве
- •Лекция 6. Уравнения прямой и плоскости в пространстве
- •6.1. Плоскость в пространстве
- •6.2. Прямая в пространстве
- •6.3. Взаимное расположение прямой и плоскости в пространстве
- •Лекция 7. Прямая линия на плоскости
- •7.1. Уравнения прямой на плоскости
- •7.2. Взаимное расположение прямых на плоскости
- •Лекция 8. Линии второго порядка и поверхности второго порядка
- •8.1. Кривые второго порядка. Основные понятия
- •8.2. Поверхности второго порядка
- •Лекция 9. Теоретико-множественные понятия в математике
- •9.1. Понятие множества. Круги Эйлера. Операции над множествами
- •9.2. Отношения и отображения как соответствия между элементами множеств. Мощность множества
- •9.3. Множество действительных чиселRи его основные подмножества
- •9.4. Окрестность точки, элементы топологии
- •Лекция 10. Действительные и комплексные числа
- •10.1. Действительные числа и их основные свойства
- •10.2. Определение комплексных чисел, комплексная плоскость, формы записи комплексных чисел
- •10.3. Операции с комплексными числами
- •Лекция 11. Многочлены
- •11.1. Многочлены. Разложение многочленов на множители
- •11.2. Рациональные дроби: правильные и неправильные. Простейшие рациональные дроби
- •11.3. Разложение правильной алгебраической дроби на сумму простейших
- •Лекция 12. Линейные пространства
- •12.1. Определение линейного пространства, свойства линейных пространств. Примеры линейных пространств
- •12.2. Подпространство линейного пространства
- •12.3. Линейно зависимые и независимые векторы. Базис и размерность линейных пространств
- •12.4. Евклидово пространство. Ортогональная система векторов. Процесс ортогонализации
- •Лекция 13. Линейные операторы
- •13.1. Определение линейного оператора и его основные свойства. Линейное пространство операторов, действующих из х в у
- •13.2. Свойства линейных операторов, действующих из х в х. Определение обратного оператора. Условие обратимости линейного оператора
- •13.3. Матрица линейного оператора
- •13.4. Переход к новому базису. Матрица перехода и её основные свойства. Связь координат вектора и матриц линейного оператора при переходе к новому базису
- •13.5. Собственные векторы и собственные значения линейного преобразования
- •13.6. Линейная модель обмена
- •Лекция 14. Квадратичные формы
- •14.2. Поведение квадратичной формы при линейном преобразовании переменных
- •14.3. Приведение квадратичной формы к каноническому виду
- •14.4. Свойства канонических форм. Знакоопределенность
- •Лекция 15. Математические структуры
- •15.1. Понятие структуры
- •15.2. Алгебраические структуры: группы и полугруппы, подгруппы, кольца и поля
- •15.3. Матричные алгебраические структуры
- •Рекомендуемая литература
Лекция 13. Линейные операторы
13.1. Определение линейного оператора и его основные свойства. Линейное пространство операторов, действующих из Х в У
13.2. Свойства линейных операторов, действующих из Х в Х. Определение обратного оператора. Условие обратимости линейного оператора
13.3. Матрица линейного оператора
13.4. Переход к новому базису. Матрица перехода и её основные свойства. Связь координат вектора и матриц линейного оператора при переходе к новому базису
13.5. Собственные векторы и собственные значения линейного преобразования
13.6. Линейная модель обмена
13.1. Определение линейного оператора и его основные свойства. Линейное пространство операторов, действующих из х в у
Пусть Х и У – линейные пространства. Элементы этих пространств будем называть векторами.
Определение
1. Оператором
 по которому каждому вектору х
по которому каждому вектору х ставится
в соответствие определенный вектор у
ставится
в соответствие определенный вектор у и
обозначается у =
и
обозначается у = или у =
или у = .
.
|
Множество Х |
Правило |
Множество У |
|
Произвольное |
Отображение |
Произвольное |
|
Векторное пространство |
Оператор |
Векторное пространство |
|
Нечисловое |
Функционал |
Числовое |
|
Числовое |
Функция |
Числовое |
Определение
2. Оператор
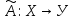 называется линейным, если для любых
х1
и х2
из множества Х и
называется линейным, если для любых
х1
и х2
из множества Х и
 выполняются соотношения:
выполняются соотношения:
 +
+
 (свойство аддитивности),
(свойство аддитивности),
2)
 =λ∙
=λ∙ (свойство однородности).
(свойство однородности).
Линейный
оператор переводит нулевой вектор
пространства Х в нулевой вектор
пространства У:

 = 0
= 0
Вектор
у =
 называется образом вектора х, а вектор
х называется прообразом вектора у.
называется образом вектора х, а вектор
х называется прообразом вектора у.
Пусть
 и
и линейные операторы, действующие из Х
в У.
линейные операторы, действующие из Х
в У.
Определение
3. Два оператора
 и
и называются равными, если для
называются равными, если для =
=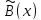 .
.
Определение
4. Суммой
двух линейных операторов
 и
и называется линейный оператор
называется линейный оператор ,
определяемый равенством:
,
определяемый равенством:
( +
+ .
.
Определение
5. Произведением
линейного оператора
 на число
на число называется линейный оператор λ
называется линейный оператор λ ,
определяемый равенством:
,
определяемый равенством:
(λ =λ∙(
=λ∙( ).
).
Определение
6. Нулевым
оператором
 называется оператор, для которого
называется оператор, для которого для
для
Нулевой оператор переводит все элементы из Х в нулевой элемент пространства У.
Определение
7. Противоположным
к оператору
 называется
линейный оператор -
называется
линейный оператор - ,
определяемый равенством: -
,
определяемый равенством: - .
.
Множество
всех линейных операторов
 обозначимL(Х,У).
Это множество с указанными выше операциями
суммы операторов и умножения на скаляр
оператора, нулевым оператором
обозначимL(Х,У).
Это множество с указанными выше операциями
суммы операторов и умножения на скаляр
оператора, нулевым оператором
 и противоположным оператором образует
векторное (линейное) пространство.
и противоположным оператором образует
векторное (линейное) пространство.
Примеры линейных операторов
Х=У= Rn ,
 Rn
отображение у = αх
Rn
отображение у = αх
 Rn
представляет собой умножение вектора
на число и является преобразованием
подобия;
Rn
представляет собой умножение вектора
на число и является преобразованием
подобия;Х- множество матриц-столбцов размера n⤫1,
У- множество матриц-столбцов размера m⤫1,
Отображение У=А∙Х представляет собой умножение матрицы А размера m⤫n на столбцы Х размера n⤫1;
Числовая функция у = к∙х.
13.2. Свойства линейных операторов, действующих из х в х. Определение обратного оператора. Условие обратимости линейного оператора
Определение1.
Линейный оператор
 называется линейным преобразованием
пространства Х.
называется линейным преобразованием
пространства Х.
Изучим подробнее свойства линейных преобразований L(Х,Х).
Определение
2. Единичным
или тождественным оператором называется
линейный оператор, который
 ставит в соответствие этот же вектор
х и обозначается
ставит в соответствие этот же вектор
х и обозначается ,
,
Определение
3. Произведением
операторов
 и
и L(Х,Х)
называется оператор
L(Х,Х)
называется оператор ∙
∙ ,
действующий по правилу: (
,
действующий по правилу: ( ∙
∙ .
.
В
общем случае
 ∙
∙ ∙
∙ .
.
Свойства
λ∙(
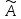 ∙
∙ ∙
∙ ;
;(



 ;
;(


Определение
4. Линейный
оператор
 называется обратным для оператора
называется обратным для оператора L(Х,Х)
, если
L(Х,Х)
, если
 ∙
∙ ∙
∙
 .
.
Обратный
оператор для оператора
 обозначается символом
обозначается символом Из определения следует, что
Из определения следует, что
Если
 Если
оператор
Если
оператор имеет обратный, то из условия
имеет обратный, то из условия следует, что
следует, что =
= и потому х=0.
и потому х=0.
 Линейный
оператор
Линейный
оператор
 L(Х,Х)
действует в векторном пространстве Х
взаимно однозначно, если для
L(Х,Х)
действует в векторном пространстве Х
взаимно однозначно, если для
 1,
х2
1,
х2 1
1 х2
соответствующие значения у1
=
х2
соответствующие значения у1
=


 .
.
Теорема.
Для того, чтобы линейный оператор
 L(Х,Х)
имел обратный
L(Х,Х)
имел обратный
 ,
необходимо и достаточно, чтобы
,
необходимо и достаточно, чтобы действовал взаимно однозначно их Х в
Х.
действовал взаимно однозначно их Х в
Х.
