- •Содержание
- •Лекция 1. Матрицы и определители n-го порядка.
- •1.1. Матрицы, их виды, линейные операции над матрицами
- •1.2. Умножение матриц
- •1.3 Определителиn-го порядка и их свойства
- •1.4. Обратная матрица
- •Лекция 2. Системы линейных уравнений и их решение
- •2.1. Системыmлинейных уравнений сnнеизвестными. Основные понятия
- •2.2. Решение системnлинейных уравнений сnнеизвестными по формулам Крамера
- •2.3. Решение системnлинейных уравнений сnнеизвестными матричным способом
- •2.4. Решение системmлинейных уравнений сnнеизвестными методом Гаусса
- •2.5. Ранг матрицы. Теорема Кронекера-Капелли
- •2.6. Однородные системы
- •Лекция 3. Решение матричных уравнений
- •Замечания.
- •1) При решении необходимо определить тип матричного уравнения и метод его решения.
- •3.2. Собственные векторы и собственные значения матрицы
- •3.3. Модель Леонтьева многоотраслевой экономики
- •Лекция 4. Векторы на плоскости и в пространстве
- •4.1. Векторы и линейные операции над ними
- •1) ; 2)Если;
- •3) Если; 4)
- •4.2. Проекция вектора на ось
- •4.3. Скалярное произведение векторов
- •4.4. Векторное произведение векторов
- •4.5 Смешанное произведение векторов
- •Лекция 5. Координатный метод
- •5.1. Системы координат на плоскости
- •5.2.Системы координат в пространстве
- •Лекция 6. Уравнения прямой и плоскости в пространстве
- •6.1. Плоскость в пространстве
- •6.2. Прямая в пространстве
- •6.3. Взаимное расположение прямой и плоскости в пространстве
- •Лекция 7. Прямая линия на плоскости
- •7.1. Уравнения прямой на плоскости
- •7.2. Взаимное расположение прямых на плоскости
- •Лекция 8. Линии второго порядка и поверхности второго порядка
- •8.1. Кривые второго порядка. Основные понятия
- •8.2. Поверхности второго порядка
- •Лекция 9. Теоретико-множественные понятия в математике
- •9.1. Понятие множества. Круги Эйлера. Операции над множествами
- •9.2. Отношения и отображения как соответствия между элементами множеств. Мощность множества
- •9.3. Множество действительных чиселRи его основные подмножества
- •9.4. Окрестность точки, элементы топологии
- •Лекция 10. Действительные и комплексные числа
- •10.1. Действительные числа и их основные свойства
- •10.2. Определение комплексных чисел, комплексная плоскость, формы записи комплексных чисел
- •10.3. Операции с комплексными числами
- •Лекция 11. Многочлены
- •11.1. Многочлены. Разложение многочленов на множители
- •11.2. Рациональные дроби: правильные и неправильные. Простейшие рациональные дроби
- •11.3. Разложение правильной алгебраической дроби на сумму простейших
- •Лекция 12. Линейные пространства
- •12.1. Определение линейного пространства, свойства линейных пространств. Примеры линейных пространств
- •12.2. Подпространство линейного пространства
- •12.3. Линейно зависимые и независимые векторы. Базис и размерность линейных пространств
- •12.4. Евклидово пространство. Ортогональная система векторов. Процесс ортогонализации
- •Лекция 13. Линейные операторы
- •13.1. Определение линейного оператора и его основные свойства. Линейное пространство операторов, действующих из х в у
- •13.2. Свойства линейных операторов, действующих из х в х. Определение обратного оператора. Условие обратимости линейного оператора
- •13.3. Матрица линейного оператора
- •13.4. Переход к новому базису. Матрица перехода и её основные свойства. Связь координат вектора и матриц линейного оператора при переходе к новому базису
- •13.5. Собственные векторы и собственные значения линейного преобразования
- •13.6. Линейная модель обмена
- •Лекция 14. Квадратичные формы
- •14.2. Поведение квадратичной формы при линейном преобразовании переменных
- •14.3. Приведение квадратичной формы к каноническому виду
- •14.4. Свойства канонических форм. Знакоопределенность
- •Лекция 15. Математические структуры
- •15.1. Понятие структуры
- •15.2. Алгебраические структуры: группы и полугруппы, подгруппы, кольца и поля
- •15.3. Матричные алгебраические структуры
- •Рекомендуемая литература
13.3. Матрица линейного оператора
Пусть
Х – линейное пространство с базисом е
= (е1
,
е2
, …
, еn
) .
Тогда
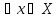 можно представить в виде
можно представить в виде
x
= х1
е1
+
х2
е2
+ …
+ хn
еn
= (1)
(1)
Формула
(1) представляет собой разложение вектора
х по базису е.
Пусть
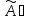 L(Х,Х)
, тогда
L(Х,Х)
, тогда
 =
= х1
е1
+
х2
е2
+ …
+ хn
еn
) =
х1
е1
+
х2
е2
+ …
+ хn
еn
) =
х1
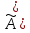 е1
)
е1
)
 х2
х2
 е2
) + …+
хn
е2
) + …+
хn
 еn
) =
еn
) = (2)
(2)
Элемент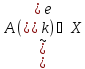 ,
так как
,
так как . Посколькуе
= (е1
,
е2
, …
, еn
) –
базис,
то вектор
. Посколькуе
= (е1
,
е2
, …
, еn
) –
базис,
то вектор
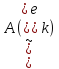 можно
разложить по этому базису:
можно
разложить по этому базису:
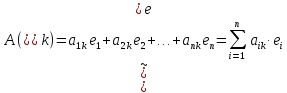 ,
(3)
,
(3)
где
 -
коэффициенты разложения вектора
-
коэффициенты разложения вектора по базису
по базису
е = (е1 , е2 , … , еn ) .
Равенство (2) с помощью представления (3) можно теперь записать в другой форме
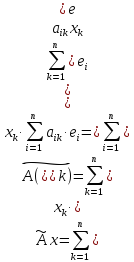
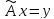 и
элемент у
имеет координаты в базисе е:
и
элемент у
имеет координаты в базисе е:
y=
у1
е1
+
у2
е2
+ …
+ уn
еn
=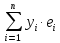 , тогда
, тогда
|
|
, где i.k =1,2,…, n. (4)
Рассмотрим
квадратную матрицу порядка п
А=(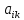 ),i,k=1,2,…,
n.
Эта матрица называется матрицей линейного
оператора
),i,k=1,2,…,
n.
Эта матрица называется матрицей линейного
оператора
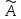 в базисее.
в базисее.
Примеры:
Х=R2, A =
 , X=
, X=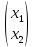 ,
Y=
,
Y=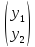 ,
A∙X=Y,
,
A∙X=Y,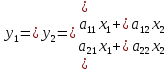 ;
;Х=R3 , А=
 .
.
Теорема.
Пусть в
линейном пространстве Х задан базис
е = (е1
,
е2
, …
, еn
)
и пусть А=(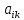 )
– квадратная матрица порядкап.
Тогда существует единственный линейный
оператор
)
– квадратная матрица порядкап.
Тогда существует единственный линейный
оператор
 , матрицей которого в базисе
, матрицей которого в базисе
е = (е1 , е2 , … , еn ) является матрица А.
13.4. Переход к новому базису. Матрица перехода и её основные свойства. Связь координат вектора и матриц линейного оператора при переходе к новому базису
Пусть
е = (е1
,
е2
, …
, еn
) –
старый базис,
 )
– в линейном
пространстве Х размерности
п.
Каждый из векторов нового базиса можно
выразить через векторы старого базиса:
)
– в линейном
пространстве Х размерности
п.
Каждый из векторов нового базиса можно
выразить через векторы старого базиса:
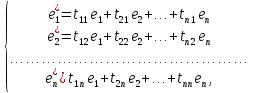
а также представить в матричной форме
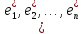 )
= (е1
,
е2
, …
, еn
) ∙
)
= (е1
,
е2
, …
, еn
) ∙

или
в матричной форме
 е ∙ Т ,
где
е ∙ Т ,
где
 -
матрица перехода от старого базиса е
к новому базису
-
матрица перехода от старого базиса е
к новому базису
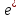 .
.
Замечание.
Координаты разложения векторов нового
базиса
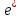 по старому
базису
е
в матрице перехода располагаются по
столбцам.
по старому
базису
е
в матрице перехода располагаются по
столбцам.
Пример.

Матрица
перехода от базиса е
к базису
 имеет
вид Т=
имеет
вид Т=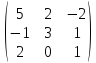 .
.
Если
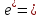 е ∙ Т , то
е
=
е ∙ Т , то
е
=
 ,где обратная
к матрице Т матрица
,где обратная
к матрице Т матрица
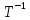 является
матрицей перехода от нового базиса
является
матрицей перехода от нового базиса
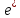 к старому
базису е
.
к старому
базису е
.
Свойства матрицы перехода
Матрица перехода Т от старого базиса к новому является невырожденной, т.е. det T
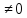 .
.Матрица перехода от нового базиса к старому имеет вид
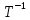 .
.Координаты вектора х в разных базисах связаны матрицей перехода.
Пусть
Х
=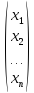 –
координаты вектора х в старом базисее ,
т.е.
–
координаты вектора х в старом базисее ,
т.е.
х
=
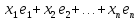 ,а Х/
,а Х/
 -координаты
вектора х в новом базисе
-координаты
вектора х в новом базисе
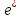 , т.е. х
=
, т.е. х
=
 а
Т-
матрица перехода от базиса е
к базису
а
Т-
матрица перехода от базиса е
к базису
 ,
тогда
,
тогда
Х = Т ∙ Х/ и Х/ = Т-1 ∙ Х . (5)
Формулы (5) представляют собой связь координат вектора в старом и новом базисах через матрицу перехода.
Пример.
Векторы х=(1,3,-2),
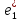 =(1,1,0),
=(1,1,0),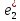 =(1,0,1),
=(1,0,1),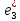 =
(0,1,1) заданы координатами в старом базисее1
,
е2
,
е3
. Найти
координаты вектора х в новом базисе
=
(0,1,1) заданы координатами в старом базисее1
,
е2
,
е3
. Найти
координаты вектора х в новом базисе
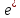 .
.
Решени.
х
=

 Матрица
перехода Т=
Матрица
перехода Т=
 от базисае
от базисае
к
базису
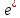 .
.
Х/
= Т-1
∙ Х =
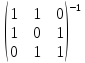 ∙
∙ =
= ,т.е.
х =
,т.е.
х =

Рассмотрим поведение линейного оператора при замене базиса: при переходе от старого базиса е к новому базису
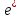 матрица А
линейного оператора
матрица А
линейного оператора
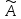 изменяется, а определитель матрицы
оператора сохраняет свою величину.
Оператор
изменяется, а определитель матрицы
оператора сохраняет свою величину.
Оператор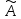 описывается различными матрицами в
разных базисах, что демонстрирует
различие между матрицей и оператором.
описывается различными матрицами в
разных базисах, что демонстрирует
различие между матрицей и оператором.
Пусть
А
– матрица линейного оператора
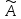 в базисе е
, А/
- матрица линейного оператора
в базисе е
, А/
- матрица линейного оператора
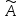 в базисе
в базисе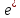 , тогда
, тогда
А/ = Т-1 ∙ А ∙ Т и А = Т∙ А/ ∙ Т-1 , (6)
причем det A=det А/ . Формулы (6) устанавливают связь между матрицами линейного оператора в разных базисах.
Замечание.
1)
Понятие линейного оператора
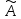 не тождественно понятию матрицы. Один
и тот же оператор может описываться
разными матрицами.
не тождественно понятию матрицы. Один
и тот же оператор может описываться
разными матрицами.
2) Подбором нового базиса ( и матрицы перехода Т ) можно привести матрицу линейного оператора к различным формам ( например, треугольной, диагональной).
Пример.
В базисе е
линейный оператор
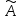 задан матрицей А=
задан матрицей А= . Найти матрицу оператора
. Найти матрицу оператора в новом базисе
в новом базисе ,
связанном
со старым базисом матрицей перехода Т=
,
связанном
со старым базисом матрицей перехода Т=
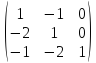 :е
:е .
.
Решение.
А/
= Т-1
∙ А ∙ Т = =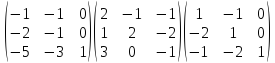 =
=
\