
- •Содержание
- •Лекция 1. Матрицы и определители n-го порядка.
- •1.1. Матрицы, их виды, линейные операции над матрицами
- •1.2. Умножение матриц
- •1.3 Определителиn-го порядка и их свойства
- •1.4. Обратная матрица
- •Лекция 2. Системы линейных уравнений и их решение
- •2.1. Системыmлинейных уравнений сnнеизвестными. Основные понятия
- •2.2. Решение системnлинейных уравнений сnнеизвестными по формулам Крамера
- •2.3. Решение системnлинейных уравнений сnнеизвестными матричным способом
- •2.4. Решение системmлинейных уравнений сnнеизвестными методом Гаусса
- •2.5. Ранг матрицы. Теорема Кронекера-Капелли
- •2.6. Однородные системы
- •Лекция 3. Решение матричных уравнений
- •Замечания.
- •1) При решении необходимо определить тип матричного уравнения и метод его решения.
- •3.2. Собственные векторы и собственные значения матрицы
- •3.3. Модель Леонтьева многоотраслевой экономики
- •Лекция 4. Векторы на плоскости и в пространстве
- •4.1. Векторы и линейные операции над ними
- •1) ; 2)Если;
- •3) Если; 4)
- •4.2. Проекция вектора на ось
- •4.3. Скалярное произведение векторов
- •4.4. Векторное произведение векторов
- •4.5 Смешанное произведение векторов
- •Лекция 5. Координатный метод
- •5.1. Системы координат на плоскости
- •5.2.Системы координат в пространстве
- •Лекция 6. Уравнения прямой и плоскости в пространстве
- •6.1. Плоскость в пространстве
- •6.2. Прямая в пространстве
- •6.3. Взаимное расположение прямой и плоскости в пространстве
- •Лекция 7. Прямая линия на плоскости
- •7.1. Уравнения прямой на плоскости
- •7.2. Взаимное расположение прямых на плоскости
- •Лекция 8. Линии второго порядка и поверхности второго порядка
- •8.1. Кривые второго порядка. Основные понятия
- •8.2. Поверхности второго порядка
- •Лекция 9. Теоретико-множественные понятия в математике
- •9.1. Понятие множества. Круги Эйлера. Операции над множествами
- •9.2. Отношения и отображения как соответствия между элементами множеств. Мощность множества
- •9.3. Множество действительных чиселRи его основные подмножества
- •9.4. Окрестность точки, элементы топологии
- •Лекция 10. Действительные и комплексные числа
- •10.1. Действительные числа и их основные свойства
- •10.2. Определение комплексных чисел, комплексная плоскость, формы записи комплексных чисел
- •10.3. Операции с комплексными числами
- •Лекция 11. Многочлены
- •11.1. Многочлены. Разложение многочленов на множители
- •11.2. Рациональные дроби: правильные и неправильные. Простейшие рациональные дроби
- •11.3. Разложение правильной алгебраической дроби на сумму простейших
- •Лекция 12. Линейные пространства
- •12.1. Определение линейного пространства, свойства линейных пространств. Примеры линейных пространств
- •12.2. Подпространство линейного пространства
- •12.3. Линейно зависимые и независимые векторы. Базис и размерность линейных пространств
- •12.4. Евклидово пространство. Ортогональная система векторов. Процесс ортогонализации
- •Лекция 13. Линейные операторы
- •13.1. Определение линейного оператора и его основные свойства. Линейное пространство операторов, действующих из х в у
- •13.2. Свойства линейных операторов, действующих из х в х. Определение обратного оператора. Условие обратимости линейного оператора
- •13.3. Матрица линейного оператора
- •13.4. Переход к новому базису. Матрица перехода и её основные свойства. Связь координат вектора и матриц линейного оператора при переходе к новому базису
- •13.5. Собственные векторы и собственные значения линейного преобразования
- •13.6. Линейная модель обмена
- •Лекция 14. Квадратичные формы
- •14.2. Поведение квадратичной формы при линейном преобразовании переменных
- •14.3. Приведение квадратичной формы к каноническому виду
- •14.4. Свойства канонических форм. Знакоопределенность
- •Лекция 15. Математические структуры
- •15.1. Понятие структуры
- •15.2. Алгебраические структуры: группы и полугруппы, подгруппы, кольца и поля
- •15.3. Матричные алгебраические структуры
- •Рекомендуемая литература
Лекция 2. Системы линейных уравнений и их решение
2.1. Системы m линейных уравнений с n неизвестными. Основные понятия
2.2. Решение систем n линейных уравнений с n неизвестными по формулам Крамера
2.3. Решение систем n линейных уравнений с n неизвестными матричным способом
2.4. Решение систем m линейных уравнений с n неизвестными методом Гаусса
2.5. Ранг матрицы. Теорема Кронекера-Капелли
2.6. Однородные системы
2.1. Системыmлинейных уравнений сnнеизвестными. Основные понятия
Определение. Уравнение называется линейным, если оно содержит неизвестные в первой степени и не содержит произведения неизвестных.
Определение. Системой m линейных уравнений с n неизвестными называется система вида:
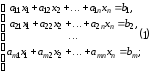 ,
,
где
x1,
x2
… xn
– неизвестные;
 -
коэффициенты,
-
коэффициенты,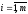 ,
,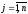 ,
,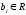 -
свободные члены.
-
свободные члены.
Определение. Решением системы (1) называется упорядоченная совокупность n действительных чисел (x1(0), x2(0)… xn(0)), при подстановке которых в систему каждое уравнение системы обращается в верное равенство.
Определение. Система (1) называется совместной, если она имеет хотя бы одно решение; и несовместной, если она не имеет решений.
Все совместные системы делятся на два вида: определённые и неопределённые.
Определение. Совместная система называется определённой, если она имеет единственное решение; и неопределённой, если она имеем более одного решения.
Определение.
Система называется квадратной, если
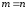 .
.
Определение.
Система (1) называется однородной, если
все
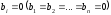 ,
и неоднородной, если хотя бы одно
,
и неоднородной, если хотя бы одно .
.
Рассмотрим однородную систему n x n:
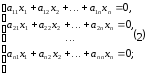 .
.
Однородная
система всегда совместна, так как имеет
тривиальное решение:
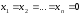 .
Также система (2) может иметь ненулевые
решения.
.
Также система (2) может иметь ненулевые
решения.
Теорема 1. Для того чтобы система (2) имела только нулевое решение, необходимо и достаточно, чтобы главный определитель этой системы был отличен от нуля.
Теорема 2. Для того чтобы система (2) имела ненулевые решения, необходимо и достаточно, чтобы главный определитель этой системы был равен нулю.
2.2. Решение системnлинейных уравнений сnнеизвестными по формулам Крамера
Формулы
Крамера удобно применять при решении
систем n
линейных уравнений с n
неизвестными при

Для
системы (2)
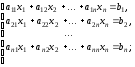 введём дополнительные понятия.
введём дополнительные понятия.
Определитель
 ,
составленный из коэффициентов при
неизвестных, называетсяглавным.
,
составленный из коэффициентов при
неизвестных, называетсяглавным.
Определитель
 ,
получаемый из главного определителя
заменойк-го
столбца столбцом свободных членов,
называется вспомогательным
(к=1,2,…n).
,
получаемый из главного определителя
заменойк-го
столбца столбцом свободных членов,
называется вспомогательным
(к=1,2,…n).
Теорема.
Если главный определитель системы (2)
не равен нулю, то система (2) имеет
единственное решение, которое находится
по формулам Крамера
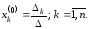
Замечания.
1.
Если в системе (2)
 ,
а хотя бы один из вспомогательных
определителей
,
а хотя бы один из вспомогательных
определителей ,
то система (2) несовместна.
,
то система (2) несовместна.
2.
Если
 и все вспомогательные определители
и все вспомогательные определители ,
то система имеет бесконечное множество
решений (в этом случае необходимо
дополнительное исследование) или
несовместна.
,
то система имеет бесконечное множество
решений (в этом случае необходимо
дополнительное исследование) или
несовместна.
Пример:Решить систему уравнений, пользуясь формулами Крамера.


2.3. Решение системnлинейных уравнений сnнеизвестными матричным способом
Рассмотрим систему уравнений (2). Составим матрицу коэффициентов при неизвестных, матрицу-столбец из неизвестных и матрицу-столбец свободных членов:
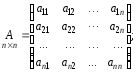
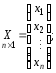
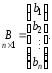
Система
(2) примет вид матричного уравнения
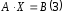 .
.
Пусть
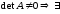 обратная
матрицаA-1.
Умножив обе части уравнения (3) на A-1
слева, получим решение уравнения (3):
обратная
матрицаA-1.
Умножив обе части уравнения (3) на A-1
слева, получим решение уравнения (3):
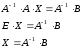
Замечание.
Рассмотрим решение матричных уравнений иного вида.
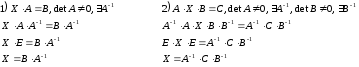
Если
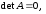 тогда система решается другим способом.
тогда система решается другим способом.
Пример. Решить матричное уравнение
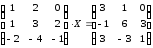
Решение
1)
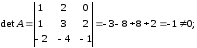
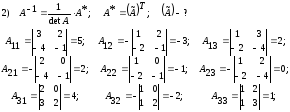

 .
.
Ответ:

