
- •Содержание
- •Лекция 1. Матрицы и определители n-го порядка.
- •1.1. Матрицы, их виды, линейные операции над матрицами
- •1.2. Умножение матриц
- •1.3 Определителиn-го порядка и их свойства
- •1.4. Обратная матрица
- •Лекция 2. Системы линейных уравнений и их решение
- •2.1. Системыmлинейных уравнений сnнеизвестными. Основные понятия
- •2.2. Решение системnлинейных уравнений сnнеизвестными по формулам Крамера
- •2.3. Решение системnлинейных уравнений сnнеизвестными матричным способом
- •2.4. Решение системmлинейных уравнений сnнеизвестными методом Гаусса
- •2.5. Ранг матрицы. Теорема Кронекера-Капелли
- •2.6. Однородные системы
- •Лекция 3. Решение матричных уравнений
- •Замечания.
- •1) При решении необходимо определить тип матричного уравнения и метод его решения.
- •3.2. Собственные векторы и собственные значения матрицы
- •3.3. Модель Леонтьева многоотраслевой экономики
- •Лекция 4. Векторы на плоскости и в пространстве
- •4.1. Векторы и линейные операции над ними
- •1) ; 2)Если;
- •3) Если; 4)
- •4.2. Проекция вектора на ось
- •4.3. Скалярное произведение векторов
- •4.4. Векторное произведение векторов
- •4.5 Смешанное произведение векторов
- •Лекция 5. Координатный метод
- •5.1. Системы координат на плоскости
- •5.2.Системы координат в пространстве
- •Лекция 6. Уравнения прямой и плоскости в пространстве
- •6.1. Плоскость в пространстве
- •6.2. Прямая в пространстве
- •6.3. Взаимное расположение прямой и плоскости в пространстве
- •Лекция 7. Прямая линия на плоскости
- •7.1. Уравнения прямой на плоскости
- •7.2. Взаимное расположение прямых на плоскости
- •Лекция 8. Линии второго порядка и поверхности второго порядка
- •8.1. Кривые второго порядка. Основные понятия
- •8.2. Поверхности второго порядка
- •Лекция 9. Теоретико-множественные понятия в математике
- •9.1. Понятие множества. Круги Эйлера. Операции над множествами
- •9.2. Отношения и отображения как соответствия между элементами множеств. Мощность множества
- •9.3. Множество действительных чиселRи его основные подмножества
- •9.4. Окрестность точки, элементы топологии
- •Лекция 10. Действительные и комплексные числа
- •10.1. Действительные числа и их основные свойства
- •10.2. Определение комплексных чисел, комплексная плоскость, формы записи комплексных чисел
- •10.3. Операции с комплексными числами
- •Лекция 11. Многочлены
- •11.1. Многочлены. Разложение многочленов на множители
- •11.2. Рациональные дроби: правильные и неправильные. Простейшие рациональные дроби
- •11.3. Разложение правильной алгебраической дроби на сумму простейших
- •Лекция 12. Линейные пространства
- •12.1. Определение линейного пространства, свойства линейных пространств. Примеры линейных пространств
- •12.2. Подпространство линейного пространства
- •12.3. Линейно зависимые и независимые векторы. Базис и размерность линейных пространств
- •12.4. Евклидово пространство. Ортогональная система векторов. Процесс ортогонализации
- •Лекция 13. Линейные операторы
- •13.1. Определение линейного оператора и его основные свойства. Линейное пространство операторов, действующих из х в у
- •13.2. Свойства линейных операторов, действующих из х в х. Определение обратного оператора. Условие обратимости линейного оператора
- •13.3. Матрица линейного оператора
- •13.4. Переход к новому базису. Матрица перехода и её основные свойства. Связь координат вектора и матриц линейного оператора при переходе к новому базису
- •13.5. Собственные векторы и собственные значения линейного преобразования
- •13.6. Линейная модель обмена
- •Лекция 14. Квадратичные формы
- •14.2. Поведение квадратичной формы при линейном преобразовании переменных
- •14.3. Приведение квадратичной формы к каноническому виду
- •14.4. Свойства канонических форм. Знакоопределенность
- •Лекция 15. Математические структуры
- •15.1. Понятие структуры
- •15.2. Алгебраические структуры: группы и полугруппы, подгруппы, кольца и поля
- •15.3. Матричные алгебраические структуры
- •Рекомендуемая литература
15.3. Матричные алгебраические структуры
Множество
 матриц
размера
матриц
размера вместе с определенными в нем операциями
сложения матриц и умножения матриц на
число образует линейное пространство.
вместе с определенными в нем операциями
сложения матриц и умножения матриц на
число образует линейное пространство.
Квадратные
матрицы
 фиксированного
размера
фиксированного
размера над заданным полемF
с операциями умножения матриц, сложения
матриц и умножения матриц на число
образуют алгебру над полем F
размерности п2
, эта алгебра
некоммутативна.
над заданным полемF
с операциями умножения матриц, сложения
матриц и умножения матриц на число
образуют алгебру над полем F
размерности п2
, эта алгебра
некоммутативна.
Во
множестве
 с умножением матриц можно определить
несколько групп:
с умножением матриц можно определить
несколько групп:
полная линейная группа - группа всех матриц с ненулевым определителем,
специальная линейная группа = множества всех матриц, определитель которых равен единице,
ортогональная группа – множество ортогональных матриц, удовлетворяющих условию А-1 = АТ .
Множество
 матриц
размера
матриц
размера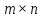 вместе с определенными в нем операциями
сложения матриц образует группу по
сложению.
вместе с определенными в нем операциями
сложения матриц образует группу по
сложению.
Рекомендуемая литература
Ильин В.А., Куркина А.В. Высшая математика. Издательство Проспект. Издательство Московского университета, 2005.
Ильин В.А., Позняк Э.Г. Линейная алгебра. М.: "Наука", 1978. Учебное пособие.
Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. М. :"Финансы и статистика", 1992. Учебник.
Карасев Ф.И., Аксютина З.М., Савельева В.И. Курс высшей математики для экономических вузов, т.1, 2. М.: "Высшая школа", 1982. Учебное пособие.
Малугин В.А. Линейная алгебра. Москва, ООО Рид Групп,2011.
Под ред. проф. Кремера Н.Ш. Высшая математика для экономистов. М., ЮНИТИ, 2006. Учебник.
Шипачев В.С. Высшая математика. М.: Высшая школа, 1998.
Лунгу К.Н., Письменный Д.Т., Федин С.Н. Сборник задач по высшей математике. 1 курс. М., АЙРИС ПРЕСС, 2003.
