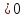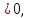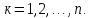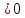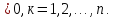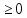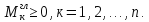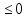83. 14.4. Свойства канонических форм. Знакоопределенность

Канонические формы, полученные разными способами, обладают некоторыми общими свойствами.

1) Закон инерции: число положительных, отрицательных и нулевых коэффициентов при квадратах переменных в канонической форме не зависит от способа приведения квадратичной формы к этому виду.

2) Свойство ранга: ранг матрицы квадратичной формы равен числу отличных от нуля коэффициентов канонической формы и не изменяется при линейных преобразованиях.

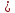Определение1. Квадратичная форма f(x) называется положи­тельно (отрицательно) определенной, если для любого не­нулевого вектора x ≠ 0 выполняется неравенствоf(x) > 0 ( f(x) 0 ).

Определение 2. Квадратичная форма f(x) называется положительно (отрицательно ) полуопределенной, если для любого ненулевого вектора

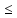x ≠ 0 выполняется неравенство f(x) 0 ( f(x) 0 ).

Определение 3. Миноры, примыкающие к левому верхнему углу матрицы, называются угловыми. Например, матрица третьего порядка имеет угловые миноры

М₁=а₁₁, М₂=. М₃=.

Определение 4. Миноры, имеющие своей диагональю главную диагональ матрицы, называются главными. Приведем эквивалентное определение: главными называются миноры, расположенные в строках и столбцах с одинаковыми номерами. У матрицы третьего порядка семь таких миноров:

три главных минора первого порядка а₁₁ , а₂₂ , а₃₃ ;

три главных минора второго порядка;

один главный минор третьего порядка .

Теорема 1. (Об определении знака квадратичной формы по собственным числам) Для того чтобы квадратичная форма была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные числа матрицы квадратичной формы были положительными (отрицательными).

При исследовании знака квадратичной формы иногда более удобно применять критерий английского математика, профессора Оксфордского университета Джеймса Джозефа Сильвестра (1814-1897).

Теорема 2. (Критерий Сильвестра об определении знака квадратичной формы по угловым минорам).

Для того чтобы квадратичная форма с матрицейбылаположительно определенной, необходимо и достаточно, чтобы все её угловые миноры

М₁=а₁₁, М₂=. …, М_n=

были положительны.

Для того чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы её угловые миноры чередовали знаки, начиная с отрицательного.

Из четырех сформулированных в критерии утверждений докажем два наиболее важные для практического применения.

1) Если все угловые миноры положительны, квадратичная форма положительно определена.

Представим квадратичную форму в каноническом виде

f(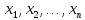)= λ₁ λ₂ λ_n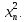

Ее матрица имеет вид

А =

Угловые миноры равны М₁=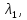

М₂=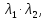

…………………..

М_n=.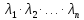

Поскольку все миноры положительны, то 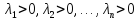, но тогда

f(х)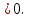

2) Если миноры чередуют знаки, начиная с отрицательного, квадратичная форма отрицательно определена.

Из соотношения М₁=и М₁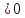 следует, что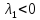, из того, что М₂=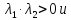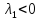вытекает, чтои т.д. Таким образом, все собственные значения отрицательны:.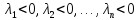

Если для исследования знакоопределенности квадратичной формы используются угловые миноры, то для изучения полуопределенности применяются главные миноры матрицы квадратичной формы.

Приведем таблицу оценки знакоопределенности квадратичной формы.

Название формы	Обозна- чение	Оценка знакоопределенности формы
		По минорам матрицы А	По собственным значениям матрицы А
Положительно определенная	f(x)	Все угловые миноры положительны: Мк	Все собственные значения положительные
Отрицательно определенная	f(x)	В угловых минорах чередуются знаки: (-1)к Мк	Все собственные значения отрицательны
Положительно полуопределенная	f(x)	Все главные миноры неотрицательны:	Все собственные значения неотрицательные
Отрицательно полуопределенная	f(x)	В главных минорах чередуются знаки	Все собственные значения неположительные
Неопределенная	f(x)		Собственные значения имеют разные знаки
Равная нулю	f(x)=0		Все собственные значения равны нулю

Пример. Квадратичную форму f(х) =

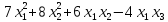
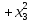
исследовать на знакоопределенность.

Решение. 1-й способ. Составим характеристическое уравнение для матрицы квадратичной формы

= - λ³ +16λ²-58λ+15=0.

Решив уравнение третьей степени, получим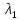= 5,.

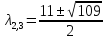Собственные числа матрицы положительны, квадратичная форма является положительно определенной.

2-й способ. Найдем угловые миноры матрицы квадратичной формы :

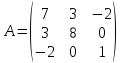М₁= 7, М₂=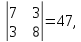М₃ =

Все угловые миноры положительны. По критерию Сильвестра имеем знакоположительную квадратичную форму.

3-й способ. Приведем квадратичную форму к каноническому виду с помощью алгебраических преобразований:

f(х) = =(.

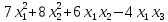
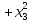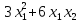
Выражение представляет собой сумму квадратов и обращается в нуль только при х₁ = х₂ = х₃ = 0. Тем самым для любого ненулевого вектора х выполняется неравенство f(x)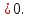 Квадратичная форма положительно определенная.