- •Содержание
- •Лекция 1. Матрицы и определители n-го порядка.
- •1.1. Матрицы, их виды, линейные операции над матрицами
- •1.2. Умножение матриц
- •1.3 Определителиn-го порядка и их свойства
- •1.4. Обратная матрица
- •Лекция 2. Системы линейных уравнений и их решение
- •2.1. Системыmлинейных уравнений сnнеизвестными. Основные понятия
- •2.2. Решение системnлинейных уравнений сnнеизвестными по формулам Крамера
- •2.3. Решение системnлинейных уравнений сnнеизвестными матричным способом
- •2.4. Решение системmлинейных уравнений сnнеизвестными методом Гаусса
- •2.5. Ранг матрицы. Теорема Кронекера-Капелли
- •2.6. Однородные системы
- •Лекция 3. Решение матричных уравнений
- •Замечания.
- •1) При решении необходимо определить тип матричного уравнения и метод его решения.
- •3.2. Собственные векторы и собственные значения матрицы
- •3.3. Модель Леонтьева многоотраслевой экономики
- •Лекция 4. Векторы на плоскости и в пространстве
- •4.1. Векторы и линейные операции над ними
- •1) ; 2)Если;
- •3) Если; 4)
- •4.2. Проекция вектора на ось
- •4.3. Скалярное произведение векторов
- •4.4. Векторное произведение векторов
- •4.5 Смешанное произведение векторов
- •Лекция 5. Координатный метод
- •5.1. Системы координат на плоскости
- •5.2.Системы координат в пространстве
- •Лекция 6. Уравнения прямой и плоскости в пространстве
- •6.1. Плоскость в пространстве
- •6.2. Прямая в пространстве
- •6.3. Взаимное расположение прямой и плоскости в пространстве
- •Лекция 7. Прямая линия на плоскости
- •7.1. Уравнения прямой на плоскости
- •7.2. Взаимное расположение прямых на плоскости
- •Лекция 8. Линии второго порядка и поверхности второго порядка
- •8.1. Кривые второго порядка. Основные понятия
- •8.2. Поверхности второго порядка
- •Лекция 9. Теоретико-множественные понятия в математике
- •9.1. Понятие множества. Круги Эйлера. Операции над множествами
- •9.2. Отношения и отображения как соответствия между элементами множеств. Мощность множества
- •9.3. Множество действительных чиселRи его основные подмножества
- •9.4. Окрестность точки, элементы топологии
- •Лекция 10. Действительные и комплексные числа
- •10.1. Действительные числа и их основные свойства
- •10.2. Определение комплексных чисел, комплексная плоскость, формы записи комплексных чисел
- •10.3. Операции с комплексными числами
- •Лекция 11. Многочлены
- •11.1. Многочлены. Разложение многочленов на множители
- •11.2. Рациональные дроби: правильные и неправильные. Простейшие рациональные дроби
- •11.3. Разложение правильной алгебраической дроби на сумму простейших
- •Лекция 12. Линейные пространства
- •12.1. Определение линейного пространства, свойства линейных пространств. Примеры линейных пространств
- •12.2. Подпространство линейного пространства
- •12.3. Линейно зависимые и независимые векторы. Базис и размерность линейных пространств
- •12.4. Евклидово пространство. Ортогональная система векторов. Процесс ортогонализации
- •Лекция 13. Линейные операторы
- •13.1. Определение линейного оператора и его основные свойства. Линейное пространство операторов, действующих из х в у
- •13.2. Свойства линейных операторов, действующих из х в х. Определение обратного оператора. Условие обратимости линейного оператора
- •13.3. Матрица линейного оператора
- •13.4. Переход к новому базису. Матрица перехода и её основные свойства. Связь координат вектора и матриц линейного оператора при переходе к новому базису
- •13.5. Собственные векторы и собственные значения линейного преобразования
- •13.6. Линейная модель обмена
- •Лекция 14. Квадратичные формы
- •14.2. Поведение квадратичной формы при линейном преобразовании переменных
- •14.3. Приведение квадратичной формы к каноническому виду
- •14.4. Свойства канонических форм. Знакоопределенность
- •Лекция 15. Математические структуры
- •15.1. Понятие структуры
- •15.2. Алгебраические структуры: группы и полугруппы, подгруппы, кольца и поля
- •15.3. Матричные алгебраические структуры
- •Рекомендуемая литература
14.2. Поведение квадратичной формы при линейном преобразовании переменных
Определение
1. Если
некоторые величины
 выражаются линейно и однородно через
величины
выражаются линейно и однородно через
величины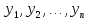 ,
т.е.
,
т.е.
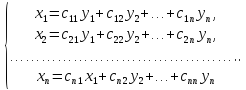 (1)
(1)
или
сокращенно
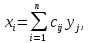 j=1, 2,…, n, где
j=1, 2,…, n, где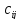 -
произвольные числа, то такое преобразование
называется линейным.
-
произвольные числа, то такое преобразование
называется линейным.
Составим
матрицы Х=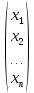 , С=
, С= ,
y=
,
y=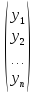 , тогда линейное преобразование можно
записать в матричной форме: Х = С∙ У, где
С- матрица линейного преобразования.
, тогда линейное преобразование можно
записать в матричной форме: Х = С∙ У, где
С- матрица линейного преобразования.
Определение
2. Линейное
преобразование (1) переменных называется
неособенным, если его матрица С неособенная
(det C
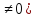 .
.
Если линейное преобразование с матрицей С неособенное, то существует обратная матрица С-1 и преобразование У=С-1∙Х называется обратным преобразованием переменных.
Определение 3. Собственные значения и собственные векторы матрицы линейного преобразования называются собственными значениями и собственными векторами линейного преобразования.
Выясним,
что произойдет с квадратичной формой
при неособенном линейном преобразовании
переменных Х = С∙ У, в этом случае мы
получим квадратичную форму от переменных
 и квадратичная форма поменяет свою
матрицу.
и квадратичная форма поменяет свою
матрицу.
Теорема 1. Если в квадратичной форме с матрицей А сделано неособенное линейное преобразование переменных Х = С∙ У, то новая квадратичная форма имеет матрицу В = СТ∙А∙С.
Доказательство.
f(X)=f(х1,
х2,…
хn
) = XT∙А∙Х.
Если Х = С∙ У, тогда квадратичная форма
в матричном виде (С∙У)Т∙А∙(С∙У)=
УТ∙СТ∙А∙С∙У=
УТ∙(СТ∙А∙С)∙У
и новая квадратичная форма от переменных
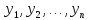 L
(y) =L(
L
(y) =L(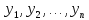 )=
УТ∙(СТ∙А∙С)∙У
имеет матрицу В = СТ∙А∙С,
что и т.д.
)=
УТ∙(СТ∙А∙С)∙У
имеет матрицу В = СТ∙А∙С,
что и т.д.
Замечание. В некоторых задачах бывает удобнее ввести обратное линейное преобразование в виде У=С-1∙Х , и если квадратичная форма L (y) имеет матрицу В, то L (y) = (С-1∙Х )TB С-1∙Х = ХT ((С-1)ТB С-1)∙Х и матрица квадратичной формы от переменных х1, х2,… хn А= (С-1)ТB С-1.
Пример
1. Как изменится
матрица квадратичной формы f(x)= -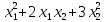 при линейном преобразовании векторов
х1=3у1-2у2,
х2=у1+2у2
?
при линейном преобразовании векторов
х1=3у1-2у2,
х2=у1+2у2
?
Решение.
Матрица
заданной квадратичной формы равна А
=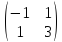 ,
а матрица С линейного оператора при
линейном преобразовании переменных
С=
,
а матрица С линейного оператора при
линейном преобразовании переменных
С= Под действием линейного оператора
матрица новой квадратичной формы от
переменныху1,
у2
будет иметь
вид B=CT∙A∙C=
Под действием линейного оператора
матрица новой квадратичной формы от
переменныху1,
у2
будет иметь
вид B=CT∙A∙C= и квадратичная форма примет более
простой вид L(y) = 32 y1y2.
и квадратичная форма примет более
простой вид L(y) = 32 y1y2.
14.3. Приведение квадратичной формы к каноническому виду
В линейной алгебре часто возникает необходимость приведения квадратичной формы к наиболее простому виду. В разобранном выше примере квадратичная форма стала проще( одно слагаемое вместо трех), в общем случае наиболее простым видом является диагональный вид квадратичной формы.
Определение1.
Квадратичная форма называется
канонической или диагональной, если
все коэффициенты при произведениях
различных переменных равны нулю, т.е.
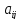 =0
при
=0
при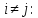
f(X)=f(х1,
х2,…
хn
) =
Матрица канонической квадратичной формы является диагональной
А
=
 .
.
Теорема 1. (Теорема Лагранжа о приведении квадратичной формы к каноническому виду) Любая квадратичная форма с помощью неособенного линейного преобразования переменных может быть приведена к каноническому виду.
Теорема 2. (Закон инерции квадратичных форм) Если вещественная квадратичная форма вещественными неособенными преобразованиями переменных приведена двумя способами к диагональному виду, то в обоих случаях число положительных, отрицательных и нулевых коэффициентов при квадратах новых переменных одно и то же.
Теорема 3. Ранг матрицы квадратичной формы равен числу отличных от нуля коэффициентов канонической формы и не изменяется при линейных преобразованиях.
Определение 2. Квадратная матрица называется ортогональной, если сумма квадратов элементов любого столбца равна единице, а сумма произведений соответствующих элементов любых двух столбцов равна нулю.
Для ортогональной матрицы Р обратная к ней совпадает с транспонированной к матрице Р: Р-1=РТ.
Определение 3. Линейное преобразование переменных называется ортогональным, если его матрица ортогональная.
Теорема 4. Каждая вещественная квадратичная форма f(х1, х2,… хn ) с матрицей А при помощи некоторого ортогонального преобразования переменных Х = Р∙ У может быть приведена к диагональному виду
L(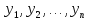 )=
λ1
)=
λ1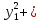 λ2
λ2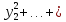 λn
λn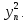
Коэффициенты λ1 , λ2 , … , λn при квадратах новых переменных с точностью до порядка расположения определены формой f(х1, х2,…, хn) однозначно, они совпадают с корнями характеристического многочлена det(A- λE)=0. Столбцы Т1 , Т2 , …, Тn ортогональной матрицы Р являются единичными собственными векторами матрицы А, соответствующими собственным числам λ1 , λ2 , … , λn .
Замечания
1) Коэффициенты λ1 , λ2 , … , λn при квадратах новых переменных являются собственными значениями матрицы А квадратичной формы f(х1, х2,…, хn).
2) Характеристический многочлен симметричной матрицы с действительными элементами имеет только действительные корни.
3)Собственные векторы симметричной матрицы, соответствующие различным собственным значениям, ортогональны.
Пример 1. Квадратичную форму f(x,y) =x2+y2+3xy привести к каноническому виду.
Решение.
Для матрицы квадратичной формы А=
 составим
характеристическое уравнение det(А-λЕ)=
составим
характеристическое уравнение det(А-λЕ)=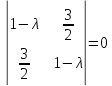 или
или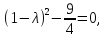 и найдем его корни: λ1=
-1/2, λ2=
5/2. Составим новую каноническую
квадратичную форму L(
и найдем его корни: λ1=
-1/2, λ2=
5/2. Составим новую каноническую
квадратичную форму L(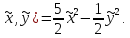
Пример
2. Привести
к каноническому виду уравнение линии
второго порядка 15х2
- 2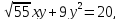 используя
теорию квадратичных форм.
используя
теорию квадратичных форм.
Решение.
Составим квадратичную форму f(x,y)=
15х2 -
2 с матрицей А=
с матрицей А=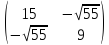 и найдем корни характеристического
уравнения det(А - λЕ) =
и найдем корни характеристического
уравнения det(А - λЕ) =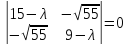 или λ2-24λ+80=0,
корни
или λ2-24λ+80=0,
корни
λ1=
20, λ2=
4. Составим новую квадратичную форму
L(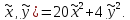
Уравнение
кривой имеет вид
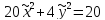 или
или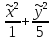 =1,
получили каноническое уравнение эллипса.
=1,
получили каноническое уравнение эллипса.
Пример
3. Квадратичную
форму f(х1,
х2,
х3)
=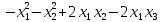 + 2
+ 2
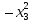 привести к диагональному виду.
привести к диагональному виду.
Решение. Вектор х задан в некотором ортонормированном базисе своими координатами х = (х1, х2, х3). Введем симметричный оператор Р (х), матрицу которого положим равной матрице квадратичной формы
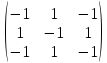 .
.
Составим характеристическое уравнение
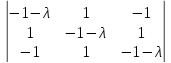 =-3λ2-λ3
= 0.
=-3λ2-λ3
= 0.
Корни
уравнения λ1=
-3, λ2,3 =
0 . В новом ортонормированном базисе,
составленном из собственных векторов
матрицы, вектор х
имеет координаты х
= (у1,
у2,
у3)
. Поэтому
f(х)=
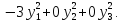
Замечание. Канонический вид квадратичной формы не является однозначно определенным. Например, заданную квадратичную форму легко преобразовать без использования симметричного оператора:
f(х1,
х2,
х3)
=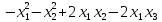 + 2
+ 2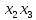
 =-
=-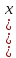 - 2
- 2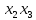
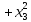 )=-(х1-х2+х3)2.
)=-(х1-х2+х3)2.
Линейное
преобразование  х1-х2+х3
приводит квадратичную форму к каноническому
виду f(х)=
-
х1-х2+х3
приводит квадратичную форму к каноническому
виду f(х)=
-
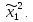 Однако в этом случае вектор
х
= (
Однако в этом случае вектор
х
= (
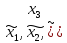 уже не является разложенным по
ортонормированному базису, составленному
из собственных векторов матрицы.
уже не является разложенным по
ортонормированному базису, составленному
из собственных векторов матрицы.
Пример
4. Квадратичную
форму f(х)
= привести к каноническому виду и выписать
ортогональное преобразование, приводящее
квадратичную форму к каноническому
виду.
привести к каноническому виду и выписать
ортогональное преобразование, приводящее
квадратичную форму к каноническому
виду.
Решение.
Матрица квадратичной формы
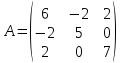 .
Составим
характеристическое уравнение
.
Составим
характеристическое уравнение
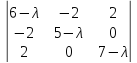 = - λ3
+18λ2-99λ+162=0,
корнями которого являются числа λ1=3,
λ2=6,
λ3=9
– собственные значения матрицы
квадратичной формы, а соответствующие
им собственные векторы имеют вид
= - λ3
+18λ2-99λ+162=0,
корнями которого являются числа λ1=3,
λ2=6,
λ3=9
– собственные значения матрицы
квадратичной формы, а соответствующие
им собственные векторы имеют вид
Х(1)=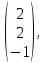 Х(2)=
Х(2)=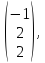 Х(3)=
Х(3)=
Собственные векторы, соответствующие различным собственным значениям, ортогональны.
Канонический вид квадратичной формы:
L( )=
3
)=
3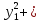 6
6 9
9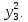
2)
Ортогональное
преобразование, приводящее квадратичную
форму к каноническому виду представлено
ортогональной матрицей, столбцы которой
являются соответствующими единичными
собственными векторами матрицы А
квадратичной формы Р=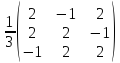 , при этом РТ∙А∙Р=
, при этом РТ∙А∙Р=