78. 13.6. Линейная модель обмена

В качестве примера математической модели экономического процесса, приводящего к понятию собственного вектора и собственного значения матрицы, рассмотрим линейную модель обмена (модель международной торговли).

Пусть имеется n стран S₁, S₂, …, S_n , национальный доход каждой из которых равен соответственно . Обозначим коэффициентами 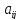долю национального дохода, которую странаS_j тратит на покупку товаров у страны S_i . Будем считать, что весь национальный доход тратится на закупку товаров либо внутри страны, либо на импорт из других стран, т.е.

(11)

Рассмотрим матрицу А =, которую называют структурной матрицей международной торговли. Согласно (11) сумма элементов любого столбца этой матрицы равна единице.

Для любой страны S_i (i= выручка от внутренней и внешней торговли составит: p_i = .

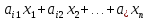Для сбалансированной торговли необходима бездефицитность торговли каждой страны S_i , т.е. выручка от торговли каждой страны должна быть не меньше её национального дохода: 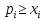(i=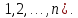

Если считать (i= , то подучим систему неравенств 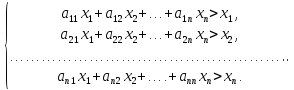(12)

Сложив все неравенства системы (12), получим после группировки

)+++…+)+…

+++…+).

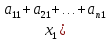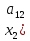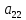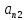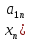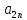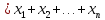Учитывая (11), выражения в скобках равны единице, и мы приходим к противоречивому неравенству.

Таким образом, неФравенство 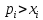(i=невозможно, и условие 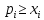принимает вид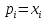(i=. С экономической точки зрения все страны не могут одновременно получать прибыль.

Введем вектор х = (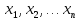)национальных доходов стран, получим матричное уравнение АХ=Х, в котором вектор х записан в виде столбца, т.е. задача свелась к отысканию собственного вектора матрицы А, отвечающего собственному значению λ=1.

Пример. Структурная матрица торговли трех стран S₁, S₂, S₃ имеет вид А = Найти соотношение национальных доходов стран для сбалансированной торговли.

Решение. Найдем собственный вектор х , отвечающий собственному значению λ=1, решив уравнение (А-Е)Х=0 или систему 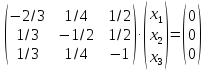методом Гаусса.

Найдем 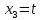, т.е.х = ().

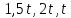Полученный результат означает, что сбалансированность торговли трех стран достигается при векторе национальных доходов х = () т.е. при соотношении национальных доходов стран 3/2:2:1 или 3:4:2.

79. Лекция 14. Квадратичные формы

14.1. Понятие квадратичной формы. Матрица квадратичной формы

14.2. Поведение квадратичной формы при линейном преобразовании переменных

14.3. Приведение квадратичной формы к каноническому виду

14.4. Свойства канонических форм. Критерий Сильвестра

80. 14.1. Понятие квадратичной формы

Определение. Квадратичной формой от n переменных х₁, х₂,… х_n называется однородный многочлен второй степени от этих переменных

f(х₁, х₂,… х_n ) =

=+

+

+

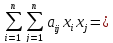
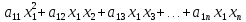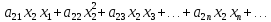
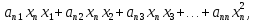
где некоторые числовые коэффициенты. Составим матрицу квадратичной формы: А=. Заметим, что коэффициенты при произведенияхи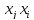равны между собой:=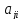, следовательно,матрица квадратичной формы симметричная А=А^Т.

Если коэффициенты квадратичной формы - вещественные числа, то квадратичная форма называется вещественной.

Пример 1. Квадратичная форма от двух переменных

f(х₁, х₂) =

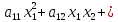
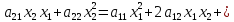
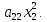
Пример 2. Квадратичная форма от трех переменных f(х₁, х₂, х₃ ) =+++.

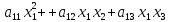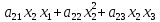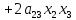Представим квадратичную форму в матричном виде:

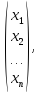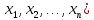обозначим Х=X^T=(, тогда

f(х₁, х₂,… х_n ) =(

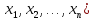
и f(х₁, х₂,… х_n ) = X^T∙А∙Х .

Пример 3. Написать матрицу квадратичной формы

1. f(х₁, х₂, х₃ )=

2. f(х₁, х₂, х₃ )= 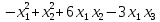+ 4

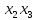
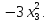
Решение. 1) А= , 2) А=.