69. 12.4. Евклидово пространство. Ортогональная система векторов. Процесс ортогонализации

Выше мы определили линейное ( векторное ) пространство, в котором можно складывать векторы и умножать их на числа, ввели понятие размерности и базиса, а теперь в данном пространстве введем метрику, т.е. способ измерять длины и углы. Это можно, например, сделать, если ввести понятие скалярного произведения.

Определение1. Линейное пространство Е называется евклидовым, если в нем определена операция скалярного произведения, которая любым двум векторам этого пространства ставит в соответствие вещественное число

(( х , у)→α) ;

операция скалярного произведения определяется следующими аксиомами:

1. ( х , у) = ( у , х) ;

2. ( х + у, z ) = ( x , z ) +( y , z ) ;

3. ( λх , у) = λ( x , y) для ;

4. ( х , x) ;( х , x) = 0 х

Величину 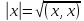называют нормой или длиной вектора х.

Вектор, длина которого равна единице, называют нормированным.

Для любых двух векторов х и у евклидова пространства справедливы

1) неравенство Коши- Буняковского |( x , y )|² ( x, x ) ∙ ( y, y )

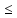2) неравенство треугольника |( x + y )|| x | +| y |.

Величину φ, определяемую из соотношения cos φ= , называют углом между векторамиx и y .

Определение 2. Два вектора называются ортогональными, если их скалярное произведение равно нулю, при этом cos φ=0 и φ= π/2.

Определение 3. Система векторов называется ортогональной, если любые два вектора этой системы ортогональны.

Определение 4. Базис (е₁ , е₂ , … , е_n) называют ортонормированным, если

(e_i., e_j ) =

Если в евклидовом пространстве размерности n задан произвольный базис ( f₁, f₂ , …, f_n), то с помощью процесса ортогонализации Грама- Шмидта по нему можно построить ортонормированный базис

(е₁ , е₂ , … , е_n) :

g₁= f₁ , е₁ = ,

g₂ = f₂ – (f₂ , е₁)∙ е₁ , е₂ = ,

g₃ = f₃ – (f₃ , е₁)∙ е₁ -(f₃ , е₂)∙ е₂ , е₃ = ,

………………………………………………………………

g_n = f_n – (f_n , е₁)∙ е₁ -(f_n , е₂)∙ е₂ -…-(f_n , е_n-1)∙ е_n-1 , е_n = .

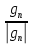В ортонормированном базисе (е₁ , е₂ , … , е_n) скалярное произведение векторов х и у находят по формуле

( х , у) = х₁у₁ + х₂у₂ + … + х_i y_i + … + x_n y_n .

Пример. Методом ортогонализации построить ортонормированный базис по базису евклидова пр-ва

₁=,₂=

₁=_{1 ,} ; ₁===

₂=₂ - (₂,₁) ∙₁=-∙

₂=

; ₁┴₂

Ответ:₁=₂=.

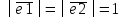70. 12.5.n- мерное арифметическое пространствоRⁿ. Скалярное произведениеn-мерных векторов, длина вектора. Угол междуn-мерными векторами

Множества всех плоских или пространственных векторов, в которых определены операции сложения векторов и умножение вектора на число, являются простейшими примерами векторных пространств. Ниже обобщается понятие вектора и дается определение векторного пространства Rⁿ.

Определение 1. n-мерным вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде х = ( х₁, х₂, … , х_i , … , x_n ), где х_i - i – я компонента вектора х.

Понятие n-мерного вектора широко используется в экономике, например некоторый набор товаров можно охарактеризовать вектором х = ( х₁, х₂, … , х_i , … , x_n ), а соответствующие цены - вектором у = ( у₁, у₂, … , у_i , … , у_n ) .

Два n-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е. х = у, если х_i = у_i , i = 1, 2, … , n.

Суммой двух векторов одинаковой размерности n называется вектор z = x + y , компоненты которого равны сумме соответствующих компонент слагаемых векторов , т.е.

z_i =x_i+y_i , I = 1,2, … , n.

Произведением вектора х на действительное число λ называется вектор u = λ х , компоненты u_i которого равны произведению λ на соответствующие компоненты вектора х, т.е. u_i = λ x_i .

Нулевым n-мерным вектором называется вектор , все компоненты которого равны нулю: О = ( 0, 0, … , 0, … 0 ) .

Противоположным к вектору х = ( х₁, х₂, … , х_i , … , x_n ) называется вектор

-х = (- х₁, - х₂, … , -х_i , … ,- x_n ) .

Определение 2. Множество всех n-мерных векторов с введенными в нем операциями сложения векторов и умножения векторов на действительные числа называется n-мерным арифметическим пространством и обозначается Rⁿ.

Пространство Rⁿ является линейным пространством.

Определение 3. Скалярным произведением двух n-мерных векторов

х = ( х₁, х₂, … , х_i , … , x_n ) и у = ( у₁, у₂, … , у_i , … , у_n ) называется

число ( х , у) = х₁у₁ + х₂у₂ + … + х_i y_i + … + x_n y_n =.

Пространство Rⁿ является евклидовым пространством, так как в нем определено скалярное произведение элементов.

Длина п-мерного вектора вычисляется по формуле =.

Угол φ между двумя п-мерными векторами определяется по формуле

φ=arccos =.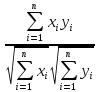