
- •Содержание
- •Лекция 1. Матрицы и определители n-го порядка.
- •1.1. Матрицы, их виды, линейные операции над матрицами
- •1.2. Умножение матриц
- •1.3 Определителиn-го порядка и их свойства
- •1.4. Обратная матрица
- •Лекция 2. Системы линейных уравнений и их решение
- •2.1. Системыmлинейных уравнений сnнеизвестными. Основные понятия
- •2.2. Решение системnлинейных уравнений сnнеизвестными по формулам Крамера
- •2.3. Решение системnлинейных уравнений сnнеизвестными матричным способом
- •2.4. Решение системmлинейных уравнений сnнеизвестными методом Гаусса
- •2.5. Ранг матрицы. Теорема Кронекера-Капелли
- •2.6. Однородные системы
- •Лекция 3. Решение матричных уравнений
- •Замечания.
- •1) При решении необходимо определить тип матричного уравнения и метод его решения.
- •3.2. Собственные векторы и собственные значения матрицы
- •3.3. Модель Леонтьева многоотраслевой экономики
- •Лекция 4. Векторы на плоскости и в пространстве
- •4.1. Векторы и линейные операции над ними
- •1) ; 2)Если;
- •3) Если; 4)
- •4.2. Проекция вектора на ось
- •4.3. Скалярное произведение векторов
- •4.4. Векторное произведение векторов
- •4.5 Смешанное произведение векторов
- •Лекция 5. Координатный метод
- •5.1. Системы координат на плоскости
- •5.2.Системы координат в пространстве
- •Лекция 6. Уравнения прямой и плоскости в пространстве
- •6.1. Плоскость в пространстве
- •6.2. Прямая в пространстве
- •6.3. Взаимное расположение прямой и плоскости в пространстве
- •Лекция 7. Прямая линия на плоскости
- •7.1. Уравнения прямой на плоскости
- •7.2. Взаимное расположение прямых на плоскости
- •Лекция 8. Линии второго порядка и поверхности второго порядка
- •8.1. Кривые второго порядка. Основные понятия
- •8.2. Поверхности второго порядка
- •Лекция 9. Теоретико-множественные понятия в математике
- •9.1. Понятие множества. Круги Эйлера. Операции над множествами
- •9.2. Отношения и отображения как соответствия между элементами множеств. Мощность множества
- •9.3. Множество действительных чиселRи его основные подмножества
- •9.4. Окрестность точки, элементы топологии
- •Лекция 10. Действительные и комплексные числа
- •10.1. Действительные числа и их основные свойства
- •10.2. Определение комплексных чисел, комплексная плоскость, формы записи комплексных чисел
- •10.3. Операции с комплексными числами
- •Лекция 11. Многочлены
- •11.1. Многочлены. Разложение многочленов на множители
- •11.2. Рациональные дроби: правильные и неправильные. Простейшие рациональные дроби
- •11.3. Разложение правильной алгебраической дроби на сумму простейших
- •Лекция 12. Линейные пространства
- •12.1. Определение линейного пространства, свойства линейных пространств. Примеры линейных пространств
- •12.2. Подпространство линейного пространства
- •12.3. Линейно зависимые и независимые векторы. Базис и размерность линейных пространств
- •12.4. Евклидово пространство. Ортогональная система векторов. Процесс ортогонализации
- •Лекция 13. Линейные операторы
- •13.1. Определение линейного оператора и его основные свойства. Линейное пространство операторов, действующих из х в у
- •13.2. Свойства линейных операторов, действующих из х в х. Определение обратного оператора. Условие обратимости линейного оператора
- •13.3. Матрица линейного оператора
- •13.4. Переход к новому базису. Матрица перехода и её основные свойства. Связь координат вектора и матриц линейного оператора при переходе к новому базису
- •13.5. Собственные векторы и собственные значения линейного преобразования
- •13.6. Линейная модель обмена
- •Лекция 14. Квадратичные формы
- •14.2. Поведение квадратичной формы при линейном преобразовании переменных
- •14.3. Приведение квадратичной формы к каноническому виду
- •14.4. Свойства канонических форм. Знакоопределенность
- •Лекция 15. Математические структуры
- •15.1. Понятие структуры
- •15.2. Алгебраические структуры: группы и полугруппы, подгруппы, кольца и поля
- •15.3. Матричные алгебраические структуры
- •Рекомендуемая литература
10.3. Операции с комплексными числами
Сумма
двух комплексных чисел 

определяется формулой:
 1
+
1
+
 2
=
(
2
=
( 1+
1+ 2)+
2)+ (
( 1+
1+ 2).
2).
При этом их радиус-векторы складываются по правилам параллелограмма:
Аналогично
 1
-
1
-
 2
=
(
2
=
( 1-
1- 2)+
2)+ (
( 1-
1- 2).
2).
Произведение
комплексных чисел
 определяют следующим образом:
определяют следующим образом:

Произведение комплексных чисел в показательной и тригонометрической формах имеет вид:
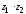 =
=
 .
.
Таким
образом:
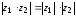 ,
аArg(
,
аArg( )
=Arg
)
=Arg 1
+ Arg
1
+ Arg 2.
2.
При
возведении в степень n
комплексного числа
 его модуль возводится в степеньn,
а аргумент увеличивается в n
раз, то есть имеем:
его модуль возводится в степеньn,
а аргумент увеличивается в n
раз, то есть имеем:

При
делении комплексных чисел в алгебраической
форме пользуются умножением числителя
и знаменателя дроби на число, сопряжённое
к знаменателю
 ,
то есть
,
то есть .
.
Пример:

В тригонометрической форму при делении комплексных чисел получают:
 (cos(
(cos(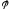 1-
1- 2)
+
2)
+
 sin(
sin( 1-
1- 2)),
то есть
2)),
то есть
 ,
а
,
а
Arg = Arg
= Arg 1
- Arg
1
- Arg 2.
2.
Определение.
 называется комплексное числоW,
такое что
называется комплексное числоW,
такое что
 .
.
Пусть
 ,r
и
,r
и
 известны,
известны, требуется определить.
требуется определить. ,
, .
Два комплексных числа, записанные в
показательной или тригонометрической
формах равны тогда и только тогда, когда
их модули равны, а аргументы отличаются
на слагаемое, кратное
.
Два комплексных числа, записанные в
показательной или тригонометрической
формах равны тогда и только тогда, когда
их модули равны, а аргументы отличаются
на слагаемое, кратное ,
то есть
,
то есть Отсюда получим
Отсюда получим
 и
и

k=0,1,2,…,n-1.
Корень n-ой
степени из комплексного числа
 имеетn
различных
значений, которые располагаются на
окружности радиуса
имеетn
различных
значений, которые располагаются на
окружности радиуса
 с центром в точке 0+0i,
а аргументы двух соседних корней
отличаются на слагаемое
с центром в точке 0+0i,
а аргументы двух соседних корней
отличаются на слагаемое
 .
.
Лекция 11. Многочлены
11.1. Многочлены. Разложение многочленов на множители
11.2. Рациональные дроби: правильные и неправильные. Простейшие рациональные дроби. Выделение целой части неправильной дроби
11.3. Разложение правильной алгебраической дроби на сумму простейших
11.1. Многочлены. Разложение многочленов на множители
Определение 1. Многочленом (полиномом) степени n от одной переменной называется выражение вида
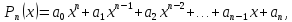 (1)
(1)
 (
( - действительные числа,n
- целое
неотрицательное число.
- действительные числа,n
- целое
неотрицательное число.
Многочлен нулевой степени (n=0) совпадает с постоянной.
Два
многочлена считают равными, если они
имеют равные коэффициенты при одинаковых
степенях
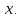
Деление
многочленов.
Разделить многочлен
 на многочленQ(
на многочленQ( – значит найти многочлены М
– значит найти многочлены М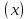 ( частное) иN(
( частное) иN( (остаток) такие, что при любом
(остаток) такие, что при любом выполняется равенство
выполняется равенство Q(
Q( М
М N(
N( ,
причем степень многочленаN(
,
причем степень многочленаN( меньше степени многочленаQ(
меньше степени многочленаQ(
Пример.
 2
2 ,
,
где
делитель Q(
N( .
.
Если
остаток от деления N( тогда
тогда Q(
Q( М
М и говорят, что
и говорят, что делится наQ(
делится наQ( нацело.
нацело.
Теорема
Безу. Остаток
от деления многочлена
 на
разность
на
разность -а
равен
-а
равен
 , т.е.
, т.е.

 –а)
М
–а)
М
 .
.
Определение
2. Число
 , для которого
, для которого ,
называется корнем многочлена
,
называется корнем многочлена .
.
Следствие.
Если а
– корень многочлена
 ,
то многочлен
,
то многочлен делится нацело на разность
делится нацело на разность -а
, т.е.
-а
, т.е.

 –а)
М
–а)
М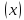 ,
где степень многочлена М
,
где степень многочлена М на единицу меньше степени многочлена
на единицу меньше степени многочлена
Разложение многочлена на множители
Если многочлен удается представить в виде произведения других многочленов, то говорят, что данный многочлен разложен на множители.
Основная
теорема алгебры.
Каждый многочлен степени n
( n имеет n
корней ( в общем случае комплексных).
имеет n
корней ( в общем случае комплексных).
Следовательно, каждый многочлен степени n можно разложить на n линейных множителей:
 ,
,
 .
.
 могут
оказаться одинаковые:
могут
оказаться одинаковые:
 ,
числа
,
числа

 кратности корней,
кратности корней, .
.
Если
корень α = β + γi
 многочлена с действительными коэффициентами
имеет кратностьk
, то корнем той же кратности k
этого многочлена будет число
многочлена с действительными коэффициентами
имеет кратностьk
, то корнем той же кратности k
этого многочлена будет число
 = β - γi
= β - γi комплексно сопряженное с корнем α .
комплексно сопряженное с корнем α .
(х-
α)(х-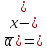 β + γi
β + γi
 β - γi
β - γi
 =((х
=((х β) – γi)((
β) – γi)(( β )+ γi
)=
β )+ γi
)=
(х β)2
– γ2
i2
= х2-
2 βх+ β2+γ2
= х2+px+q
, где p=
-2β, q=
β2+γ2,
β)2
– γ2
i2
= х2-
2 βх+ β2+γ2
= х2+px+q
, где p=
-2β, q=
β2+γ2,
p2-4q
Вывод. Каждый многочлен с действительными коэффициентами можно представить в виде произведения линейных множителей и квадратных трехчленов в степенях, равных кратностям корней:
 =
= ...
... ,
,
 где
где
 +
+ =n
,
=n
,
 -
4
-
4 j = 1,2,…, s
j = 1,2,…, s
