41. 7.2. Взаимное расположение прямых на плоскости

Рассмотрим взаимное расположение прямых в двух случаях, когда прямые заданы общими уравнениями и уравнениями с угловыми коффициентами.

1) Пусть прямые l₁ и l₂ заданы общими уравнениями:

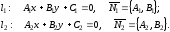
Тогда

Если – необходимое и достаточное условие параллельности прямых.

Если 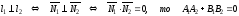необходимое и достаточное условие перпендикулярности прямых.

2) Пусть прямые l₁ и l₂ заданы уравнениями с угловыми коэффициентами:

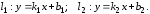
Определение. Углом между двумя пересекающимися упорядоченными прямыми l₁ и l₂ называется угол, отсчитываемый от l₁ до l₂ против движения часовой стрелки.

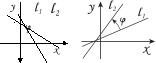
Пусть – угол между прямымиl₁ и l₂, тогда .

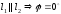Еслиили-необходимое и достаточное условие параллельности прямых.

Если , но, так как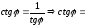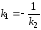-необходимое и достаточное условие перпендикулярности прямых.

43. Лекция 8. Линии второго порядка и поверхности второго порядка

8.1. Кривые второго порядка: окружность, эллипс, гипербола, парабола. Основные понятия

8.2. Поверхности второго порядка

44. 8.1. Кривые второго порядка. Основные понятия

Определение. Линия на плоскости, которая в декартовой системе координат определяется уравнением второй степени, называется линией второго порядка.

Общее уравнение линий 2-го порядка имеет вид:

Если это уравнение определяет кривую, то это может быть либо окружность, либо эллипс, либо гипербола, либо парабола.

Определение. Окружностью называется геометрическое место точек, равноудалённых от фиксированной точки, называемой центром.

Если r – радиус окружности, точка C(a, b) – центр окружности, то уравнение окружности имеет вид:

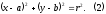
Если центр совпадает с началом координат, то уравнение окружности имеет вид:

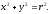
Если в уравнении (2) раскрыть скобки, то получится общее уравнение окружности, которое имеет вид: 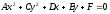, причём. Если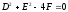, то окружность вырождается в точку с координатами. Если, то уравнение определяет мнимую окружность.

Определение. Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек F₁ и F₂, называемых фокусами, есть величина постоянная, равная 2a, причём 2a>2c, где 2c – расстояние между фокусами.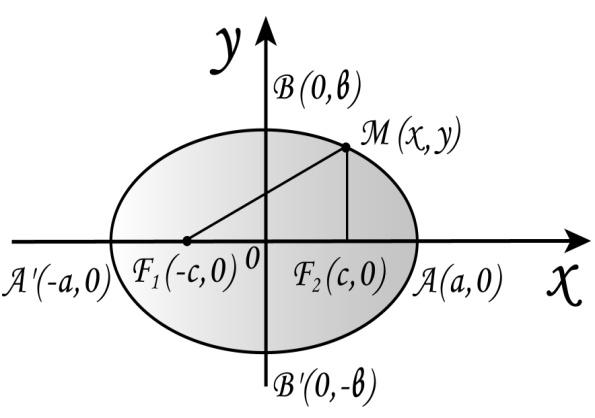

Для эллипса a>c. Если оси декартовой системы координат выбрать так, что фокусы эллипса располагаются на оси абсцисс симметрично относительно начала координат, то уравнение эллипса имеет вид:

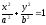–каноническое уравнение эллипса.

Точки A и A′, B и B′ называются вершинами эллипса, отрезки OA=a – большая полуось, OB – малая полуось, причём .

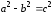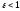Точку пересечения осей называют центром эллипса. Форма эллипса (мера его сжатия) характеризуется эксцентриситетом и, так какa>c. Если a=b, то c=0 и 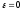, фокусы сливаются в одну точку – центр и эллипс превращается в окружность.

Если центр эллипса смещён и находится в точке C(x₁,y₁), a оси симметрии эллипса параллельны осям координат, то уравнение эллипса имеет вид:

.

Определение. Гиперболой называется геометрическое место точек плоскости, для которых модуль разности расстояний до двух фиксированных точек F₁ и F₂, называемых фокусами, есть величина постоянная, равная 2a, причём 2a<2c.

Если оси декартовой системы координат выбрать так, что фокусы гиперболы располагаются на оси абсцисс симметрично относительно начала координат, то уравнение гиперболы имеет вид: 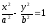– каноническое уравнение гиперболы.

Точки A(a, 0) и A′(-a, 0) – вершины гиперболы, отрезок AA′=2a – действительная ось гиперболы, отрезок BB′ – мнимая ось гиперболы. Прямоугольник со сторонами 2a и 2b, расположенный симметрично

относительно осей гиперболы и касающийся её в вершинах, называется основным прямоугольником гиперболы. Его диагонали принадлежат асимптотам гиперболы, уравнения которых 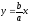и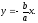

Эксцентриситет гиперболы 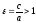, т.к.a<c. Если a=b, то гипербола является равнобочной. Если уравнение гиперболы имеет вид 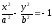, то действительной осью этой гиперболы служит отрезок оси оy равный 2b.

Гиперболы 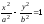иназываются сопряжёнными.

Если центр смещён и находится в точке C(x₁,y₁), a оси симметрии гиперболы параллельны осям координат, то уравнение гиперболы имеет вид:

.

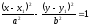Определение. Параболой называется геометрическое место точек плоскости, равноудалённых от фиксированной точки F, называемой фокусом, и фиксированной прямой, называемой директрисой.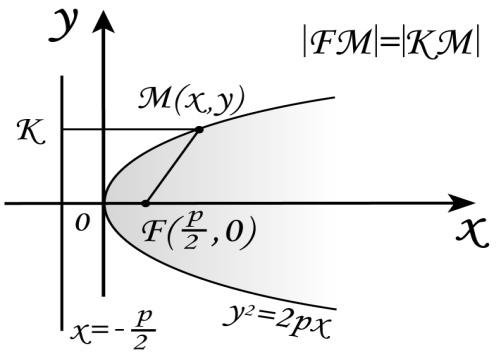

Расстояние от фокуса до директрисы равно p, p>0 – параметр параболы.

Если ось абсцисс декартовой системы координат проходит через фокус параболы перпендикулярно директрисе и направлена от директрисы к фокусу, то начало координат находится посередине между фокусом и каноническое уравнение параболы имеет вид:

.

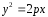Точка 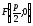– фокус параболы, прямая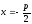– директриса параболы, точка пересечения параболы с осью называется её вершиной. Парабола имеет одну ось симметрии.

Если парабола лежит в левой полуплоскости, то её уравнение имеет вид:

.

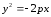Её фокус находится в точке 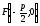и уравнение директрисы.

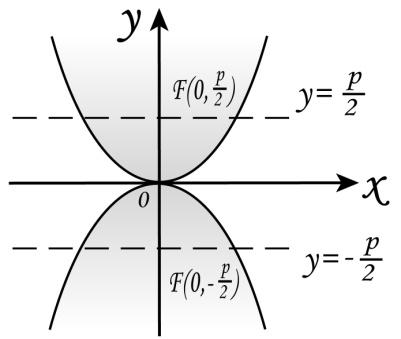
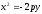Если ось параболы совмещена с осью ординат, то парабола имеет уравнение , если лежит в верхней полуплоскости, и, если лежит в нижней полуплоскости.

Уравнения смещённых парабол с вершиной в точке C(x₁,y₁) имеют вид:

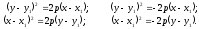
Замечание.

Если уравнение 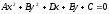определяет кривую второго порядка, то

1. при 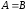эта кривая является окружностью;

2. при 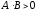эта кривая является эллипсом;

3. при эта кривая является гиперболой;

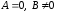4. при или при эта кривая является параболой.