
- •Содержание
- •Лекция 1. Матрицы и определители n-го порядка.
- •1.1. Матрицы, их виды, линейные операции над матрицами
- •1.2. Умножение матриц
- •1.3 Определителиn-го порядка и их свойства
- •1.4. Обратная матрица
- •Лекция 2. Системы линейных уравнений и их решение
- •2.1. Системыmлинейных уравнений сnнеизвестными. Основные понятия
- •2.2. Решение системnлинейных уравнений сnнеизвестными по формулам Крамера
- •2.3. Решение системnлинейных уравнений сnнеизвестными матричным способом
- •2.4. Решение системmлинейных уравнений сnнеизвестными методом Гаусса
- •2.5. Ранг матрицы. Теорема Кронекера-Капелли
- •2.6. Однородные системы
- •Лекция 3. Решение матричных уравнений
- •Замечания.
- •1) При решении необходимо определить тип матричного уравнения и метод его решения.
- •3.2. Собственные векторы и собственные значения матрицы
- •3.3. Модель Леонтьева многоотраслевой экономики
- •Лекция 4. Векторы на плоскости и в пространстве
- •4.1. Векторы и линейные операции над ними
- •1) ; 2)Если;
- •3) Если; 4)
- •4.2. Проекция вектора на ось
- •4.3. Скалярное произведение векторов
- •4.4. Векторное произведение векторов
- •4.5 Смешанное произведение векторов
- •Лекция 5. Координатный метод
- •5.1. Системы координат на плоскости
- •5.2.Системы координат в пространстве
- •Лекция 6. Уравнения прямой и плоскости в пространстве
- •6.1. Плоскость в пространстве
- •6.2. Прямая в пространстве
- •6.3. Взаимное расположение прямой и плоскости в пространстве
- •Лекция 7. Прямая линия на плоскости
- •7.1. Уравнения прямой на плоскости
- •7.2. Взаимное расположение прямых на плоскости
- •Лекция 8. Линии второго порядка и поверхности второго порядка
- •8.1. Кривые второго порядка. Основные понятия
- •8.2. Поверхности второго порядка
- •Лекция 9. Теоретико-множественные понятия в математике
- •9.1. Понятие множества. Круги Эйлера. Операции над множествами
- •9.2. Отношения и отображения как соответствия между элементами множеств. Мощность множества
- •9.3. Множество действительных чиселRи его основные подмножества
- •9.4. Окрестность точки, элементы топологии
- •Лекция 10. Действительные и комплексные числа
- •10.1. Действительные числа и их основные свойства
- •10.2. Определение комплексных чисел, комплексная плоскость, формы записи комплексных чисел
- •10.3. Операции с комплексными числами
- •Лекция 11. Многочлены
- •11.1. Многочлены. Разложение многочленов на множители
- •11.2. Рациональные дроби: правильные и неправильные. Простейшие рациональные дроби
- •11.3. Разложение правильной алгебраической дроби на сумму простейших
- •Лекция 12. Линейные пространства
- •12.1. Определение линейного пространства, свойства линейных пространств. Примеры линейных пространств
- •12.2. Подпространство линейного пространства
- •12.3. Линейно зависимые и независимые векторы. Базис и размерность линейных пространств
- •12.4. Евклидово пространство. Ортогональная система векторов. Процесс ортогонализации
- •Лекция 13. Линейные операторы
- •13.1. Определение линейного оператора и его основные свойства. Линейное пространство операторов, действующих из х в у
- •13.2. Свойства линейных операторов, действующих из х в х. Определение обратного оператора. Условие обратимости линейного оператора
- •13.3. Матрица линейного оператора
- •13.4. Переход к новому базису. Матрица перехода и её основные свойства. Связь координат вектора и матриц линейного оператора при переходе к новому базису
- •13.5. Собственные векторы и собственные значения линейного преобразования
- •13.6. Линейная модель обмена
- •Лекция 14. Квадратичные формы
- •14.2. Поведение квадратичной формы при линейном преобразовании переменных
- •14.3. Приведение квадратичной формы к каноническому виду
- •14.4. Свойства канонических форм. Знакоопределенность
- •Лекция 15. Математические структуры
- •15.1. Понятие структуры
- •15.2. Алгебраические структуры: группы и полугруппы, подгруппы, кольца и поля
- •15.3. Матричные алгебраические структуры
- •Рекомендуемая литература
Лекция 6. Уравнения прямой и плоскости в пространстве
6.1. Плоскость в пространстве
6.2. Прямая в пространстве
6.3. Взаимное расположение прямой и плоскости в пространстве
6.1. Плоскость в пространстве
Пусть точка M0(x0,y0,z0) принадлежит плоскости П.
Определение.
Всякий ненулевой вектор
 ,
перпендикулярный к плоскости, называется
нормальным вектором плоскости.
,
перпендикулярный к плоскости, называется
нормальным вектором плоскости.
Теорема
1. Если
плоскость проходит через точку
M0(x0,y0,z0)
и её нормальный вектор
 ,
то уравнение плоскости имеет вид:
,
то уравнение плоскости имеет вид:
 .
.
Доказательство. Пусть M(x,y,z) – текущая точка плоскости, тогда
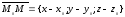 принадлежит
плоскости. Так как
принадлежит
плоскости. Так как
 -
нормальный вектор плоскости, то
-
нормальный вектор плоскости, то ,
но
,
но

Теорема
2. Всякое
линейное уравнение с тремя переменными
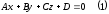 определяет плоскость в пространстве,
если хотя бы одно из трех чисел
определяет плоскость в пространстве,
если хотя бы одно из трех чисел .
.
Уравнение
(1) называется общим уравнением плоскости.
При этом, если в уравнении отсутствует
какая-либо переменная, то плоскость
параллельна соответствующей оси
координат, например: плоскость
 Если в уравнении (1)D=0,
то плоскость
Если в уравнении (1)D=0,
то плоскость
 проходит через начало координат.
проходит через начало координат.
Предположим, что в общем уравнении плоскости все коэффициенты отличны от нуля, т.е. плоскость пересекает все координатные оси и не проходит через начало координат. Преобразуем уравнение (1):




– уравнение плоскости в отрезках, где a, b, c – отрезки, которые отсекает плоскость на координатных осях оx, оy и оz соответственно.
Замечание:
Уравнение плоскости, проходящей через три точки
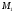 (x1,y1,z1),
(x1,y1,z1),
 (x2,y2,z2),
(x2,y2,z2),
 (x3,y3,z3),
имеет вид:
(x3,y3,z3),
имеет вид:

Уравнение плоскости, проходящей через две точки
 (x1,y1,z1)
и
(x1,y1,z1)
и
 (x2,y2,z2)
перпендикулярно плоскости
(x2,y2,z2)
перпендикулярно плоскости
 имеет вид:
имеет вид:

3)
Уравнение плоскости, проходящей через
точку M0(x0,y0,z0)
перпендикулярно двум непараллельным
плоскостям
 и
и
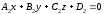 имеет
вид:
имеет
вид:

Рассмотрим взаимное расположение плоскостей в пространстве. Пусть даны две плоскости
П1:
П2:
Определение. Под углом между двумя плоскостями понимают один из двух смежных двугранных углов.
Угол
между двумя плоскостями равен углу
между нормальными векторами этих
плоскостей. Вычисляется этот угол по
формуле:

Условия
параллельности и перпендикулярности
плоскостей определяются условиями
коллинеарности и перпендикулярности
их нормальных векторов.
 – необходимое и достаточное условие
параллельности плоскостей;
– необходимое и достаточное условие
параллельности плоскостей;
 или
или
 – необходимое и достаточное условие
перпендикулярности плоскостей.
– необходимое и достаточное условие
перпендикулярности плоскостей.
Расстояние
от точки M*(x*,y*,z*)
до плоскости П: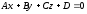
вычисляется
по формуле:
 .
.
6.2. Прямая в пространстве
Рассмотрим
прямую l
с принадлежащей ей точкой M0(x0,y0,z0).
Определение.
Всякий ненулевой вектор
 называется направляющим вектором
прямой.
называется направляющим вектором
прямой.
Положение
прямой в пространстве R3
однозначно определяется принадлежащей
ей точкой M0(x0,y0,z0)
и направляющим вектором
 .
.
Рассмотрим различные виды уравнений прямой.
Пусть M(x,y,z) – текущая точка прямой. Тогда вектор


 -
канонические
уравнения прямой.
-
канонические
уравнения прямой.
2)
Обозначим
тогда


и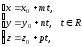 -
параметрические уравнения прямой в
пространстве.
-
параметрические уравнения прямой в
пространстве.
3)
Пусть даны две точки M1(x1,y1,z1)
и M2(x2,y2,z2)
прямой,
 Так как
Так как ,
то вектор
,
то вектор можно взять за направляющий и,
воспользовавшись каноническими
уравнениями прямой, получим:
можно взять за направляющий и,
воспользовавшись каноническими
уравнениями прямой, получим:

– уравнение прямой, проходящей через две точки.
4) Прямую в пространстве можно рассматривать как пару пересекающихся плоскостей, а именно:
система
 определяет общие уравнения прямой.
определяет общие уравнения прямой.
Рассмотрим
правила перехода от канонических
уравнений к общим и наоборот.
Так
как

Переход от общих уравнений к каноническим осуществляется таким образом:
1) выражают x через y, исключив z в (1);
2) выражают x через z, исключив y в (1);
3) составляют канонические уравнения.
Пример.
Составить канонические уравнения прямой

Решение
1. Сложив уравнения системы, получим:
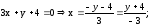
2.
Аналогично из системы
 получим
получим
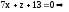

3.
Запишем канонические уравнения прямой
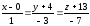 .
Полученная прямая проходит через точкуM(0,-4,-13)
и имеет направляющий вектор
.
Полученная прямая проходит через точкуM(0,-4,-13)
и имеет направляющий вектор
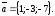
Рассмотрим взаимное расположение прямых в пространстве.
Пусть
даны две прямые:

Определение. Углом между прямыми l1 и l2 называется угол между направляющими векторами этих прямых.
Этот угол вычисляется по формуле:
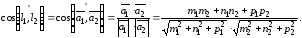
Условия параллельности и перпендикулярности прямых определяются условиями коллинеарности и перпендикулярности их направляющих векторов.
 –необходимое
и достаточное условие параллельности
прямых;
–необходимое
и достаточное условие параллельности
прямых;


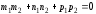
–необходимое и достаточное условие перпендикулярности прямых.
