30. 5.2.Системы координат в пространстве

Система координат в пространстве – это правило, которое устанавливает взаимно однозначное соответствие между точками пространства и упорядоченными тройками чисел, которые называют координатами заданной точки.

Аффинная система координат в пространстве

Репер < О; 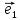,> в пространстве задает систему координат следующим образом. Каждая точка М определяет вектор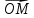, который определяет упорядоченную тройку чисел (х, у, z) равенством 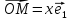+у 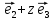. Числах,у.z являются координатами точки М, что может быть подчеркнуто записью М=М(х,у.z). Такая система координат называется косоугольной или аффинной системой координат в пространстве. Первая координата точки в такой системе координат называется абсциссой, а вторая – ординатой точки, а третья – аппликатой точки.

Ось, задаваемую точкой О и вектором называютосью абсцисс; ось, задаваемую точкой О и вектором , называютосью ординат;.

ось, задаваемую точкой О и вектором , называютосью аппликат.

Если в репер входит правая тройка векторов, то система координат называется правой. В противном случае она называется левой.

z y

M

z₀

yuyyy

x₀ x

Цилиндрическая система координат

В пространстве задана цилиндрическая система координат, если заданы плоскость П с полярной осью и ось OZ, проходящая через начало полярной оси – полюс перпендикулярно плоскости П. Обозначим через 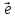- орт (единичный вектор), задающий положительное направление осиOZ.

Цилиндрической системой координат каждой точке М ставится в соответствие упорядоченная тройка чисел ρ, φ, z следующим правилом. Вектор 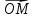разлагается в сумму:

+ z,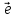

где М₁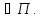 Эта сумма определяет число z . Числа ( ρ, φ ) – это полярные координаты точки М₁, 0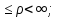0φ.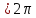

Пусть заданы цилиндрическая и правая декартова системы координат в пространстве, причем полярной осью служит ось абсцисс, а полюс О совмещен с началом О декартовой системы координат, ось OZ, проходящая через полюс , перпендикулярна плоскости П. Тогда между декартовыми координатами (х,у,z) и полярными координатами (ρ,φ,z) точки М в пространстве существует связь: ,

M(ρ,φ,z)

z

M₁

0

Cферическая система координат

В пространстве задана сферическая система координат, если заданы плоскость П с полярной осью и ось OZ, проходящая через начало полярной оси – полюс перпендикулярно плоскости П. Обозначим через - орт (единичный вектор), задающий положительное направление осиOZ.

Сферической системой координат каждой точке М ставится в соответствие упорядоченная тройка чисел следующим правилом. Вектор 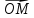разлагается в сумму:

+ z,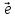

где М₁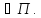 Далее сферическая система координат точке М ставит в соответствие три числа 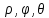, где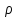- расстояние от начала полярной оси до точки М, 0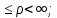- полярный угол точки М₁ , 0φ- угол между радиус-вектороми вектором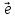, 0

Пусть заданы сферическая и правая декартова системы координат в пространстве, причем полярной осью служит ось абсцисс, а полюс О совмещен с началом О декартовой системы координат, ось OZ, проходящая через полюс , перпендикулярна плоскости П. Тогда между декартовыми координатами (х,у,z) и сферическими координатами (ρ,φ,) точки М в пространстве существует связь: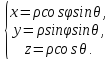

M(ρ,φ,)

M₁