Методички / Курс деталей машин

создаёт момент против направления вращения. Осевая сила Fa1 направлена с сторону основания конуса, а силу Fa2 направляют ей противоположно для уменьшения нагрузки на подшипники. Схема нагружения преобразована после приведения действующих сил к оси вала на две расчётные схемы сил,

действующих в двух плоскостях. Приведение сил выполнено по следующим правилам:

а) радиальные силы Fr проходят через ось вала, к которой они и приложены без добавления моментов;

б) осевые силы приведены к оси с добавлением сосредоточенных моментов

т = Fa·d/2; сами осевые силы изгибающего момента не создают, но участвуют в уточнённом расчёте вала и расчёте подшипников;

в) окружные силы приведены к оси с добавлением крутящего момента,

который также изгибающего момента не создаёт, но создаёт крутящий момент

Т, который участвует в расчёте диаметра опасного сечения.

г) схемы и эпюры выполнены на отдельном листе.

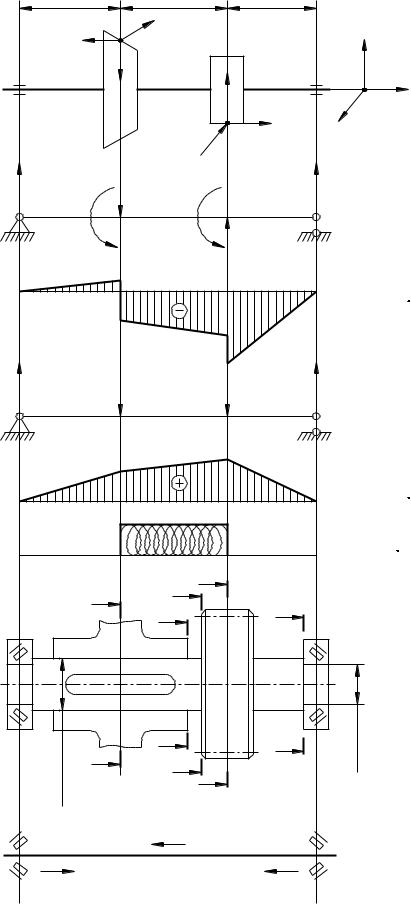
2) Определяем реакции и моменты в направлении Z. Силы, действующие в направлении Z, показаны на рис. 23.6, б. Реакции опор R1z и R2z определены из двух уравнений равновесия. Третье уравнение использовано для проверки.

Сосредоточенные моменты:

m1 = Fa1·dm2/2 = 362·171,77/2 = 31090 Н·мм = 31,1 Н·м; т2 = Fa2·d1/2 = 572·65,57/2 = 18753 Н·мм = 18,8 Н·м.

Моментное уравнение:

M0;R(lll)F(ll)Flm0

1z 2z123r212r112, откуда

R(F(ll)Flm)/(lll)

2z r212r112123

(956(7060)102703 )8753/(706050)9Н.028

Направление реакции R2z противоположно изображённому на рис. 23.6, б.

Уравнение проекций:

Z0; RFFR0, откуда

1z r1 r2 2z

RFFR102956(928)74H.

1z r1 r2 2z

Проверочный расчёт выполнен по второму моментному уравнению:

M 0; R(lll)F(ll)Flmm

2z 1z123 r123 r23 1 2

74(6050)102(6050)956503118757Нм0,Нм.96

Полученное значение близко к нулевому. Эпюры изгибающих моментов

(рис. 35, в) построены на сжатом волокне. Значения моментов Mz:

MMm51831250Нмм90;10

3z 3 1

MR(ll)Flm74(7060)10260310275Нм;

4z1z12r121

MMm275901875345943Нмм;М 0.

4z 4 2 2z

На эпюре Мz под сосредоточенными моментами будут скачки, равные моментам т1 и т2. В направлении оси х действуют силы Ft1 и Ft2 (рис. 23.6, г),

которые совмещены с вертикальной плоскостью. Реакции опор определены из двух уравнений равновесия:

M0;R(lll)F(ll)Fl0;

1x 2x123 t212 t1 откуда

R(F(ll)Fl)/(lll)256(7060)10370/(50)2H.

2xt212t1123

X0; RFFR0;откуда

1x t1 t2 2x

RFFR1032562521342H.

1x t1t2 2x

Изгибающие моменты в направлении X:

По величинам ординат эпюр Мх и Мz выявлено опасное (расчётное) сечение

4 вала. Суммарный изгибающий момент – формула (23.4):

MM2M2 112545912155Нмм.403

4 4x 4z

Приведенный момент – формула (23.5):

MMT 84014Нмм. 040

2 2121557,0

пр4 II

Диаметр вала в опасном сечении – формула (23.6):

32140411 d3 29,6мм.

55

По результатам приближённого расчёта окончательно назначены диаметры характерных сечений вала. В опасном сечении принят диаметр 36 мм, диаметр

шейки 30 мм. При диаметре вершин цилиндрической шестерни d 69,57мм

a1

принята конструкция вал-шестерня.

23.6. Уточнённый расчёт валов

Уточнённый расчёт – проверочный. Он является расчётом на сопротивление усталости. Уточнённый расчёт заключается в определении коэффициентов запаса прочности в опасных сечениях вала (рис. 23.6). Такими являются сечения, опасные по изгибающему или крутящему моменту при наличии концентраторов напряжений: посередине ступицы (концентратор напряжений – шпоночная канавка), у края ступицы (напрессовка), под подшипниками качения

(переходное сечение), на хвостовике - посередине ступицы (шпоночная канавка).

При наличии двух концентраторов расчёт ведут по более опасному. Запас сопротивления усталости по нормальным напряжениям (в основном, по изгибу):

В формулах (23.7) и (23.8):

-1 и -1 – пределы выносливости (прил. 28);

К и К – эффективные коэффициенты концентрации напряжений;

определяются по справочникам в зависимости от вида концентратора;

εσ и ετ – масштабные коэффициенты;

β – коэффициент состояния поверхности;

а и а – амплитудные напряжения цикла;

m и m – средние напряжения цикла;

ψ и ψ – коэффициенты, учитывающие чувствительность материала к асимметрии цикла.

Нормальные напряжения изменяются по симметричному циклу.

(23.10)

В формуле (23.10) М – изгибающий момент в рассчитываемом сечении.

Если принята нереверсивная работа передачи (пульсирующий цикл изменения касательных напряжений), то

,T

, . (23.11)

a m max

W

p

T

При реверсивной работе ; 0.

a max m

W

p

Допускаемый коэффициент запаса прочности [s] = 1,7. Расчёт вала на жёсткость можно не проводить при s 2,5. Но при s 3,5 конструкция неэкономична. Таким образом, рекомендуется [s] = 2,5…3,5.

Пример 23.3. Выполнить уточнённый расчёт промежуточного вала двухступенчатого коническо-цилиндрического редуктора по исходным данным примера 23.2: крутящий момент TII = 84 Н·м, диаметр головки d1 = 36 мм,

диаметр шейки d2 = 30 мм, осевые усилия Fa1 = 362 Н, Fa2 = 572 Н, расстояния между линиями действия сил (из эскизной компоновки): l1 = 70 мм, l2 = 60 мм, l3 =

50 мм, длина ступицы вала колеса lст = 50 мм. Ширина венца цилиндрической шестерни b = 36 мм, ширина подшипника качения В = 16 мм. Диаметры цилиндрической шестерни: da1 = 69,57 мм, df1 = 60,57 мм. Шероховатость поверхностей Ra = 2,5 мкм. Материал вала сталь 40Х, термообработка – улучшение. Работа нереверсивная.

Решение.

1) Приняты расчётные сечения А-А (концентратор напряжений – шпоночная канавка), Б-Б (напрессовка), В-В (переходное сечение), Г-Г (зубья), Д-

Д (переходное сечение и напрессовка, рис. 23.6, ж). В примере рассмотрено сечение Б-Б. Его расстояние от опоры 1: l Б-Б = l1 + 0,5 lст = 70 + 0,5·50 = 95 мм.

2) Изгибающий момент в расчётном сечении определён по линейной интерполяции в зависимости от положения на участке Б-Г длиной l2 .

М zБ-Б = М3ʹz + Mz(0,5 lст/ l2) = 25910 + 1680·(0,5·50/60) = 26610 Н·мм.

Аналогично определён момент в направлении Х:

М хБ-Б = 95940 + (112540 – 95940)·(0,5·50/60) = 102857 Н·мм.

Результирующий изгибающий момент:

MM2M2 102857266101062Нмм.

Б xБzБ

3)Осевая нагрузка: Fa = Fa2 - Fa1 = 572 – 362 = 210 H.

4)Параметры сечения. Площадь:

АБ-Б = АВ-В = πd2/4 = π·362/4 = 1018 мм2.

Момент сопротивления:

WБ-Б = WВ-В = πd3/32 = π·363/32 = 4580 мм3.

Полярный момент сопротивления:

WрБ-Б = WрВ-В = π·363/16 = 9161 мм3.

5)Характеристики материала вала: -1 = 410 МПа, -1 = 240 МПа, = 0,1;

=0,05 (прил. 28).

6)Коэффициенты [11]: β = 0,9; К / = 4 (для посадки H7/s6); Кτ/τ = 1

+0,6·4 = 3,4.

7) Амплитудные и средние напряжения в сечении:

M/W106243//;9,214850/ МПаFA210,М

aи mp(c)a ;

0,5Т/W0,584103/91614,58МПа.

amax

8) Коэффициенты запаса:

a m

[δ]= 0,01m – для валов цилиндрических зубчатых передач, где m – модуль зацепления;

[δ]= (0,0002…0,0003)·L – в станкостроении для валов общего назначения,

где L – расстояние между опорами;

[δ] = 0,1δв – для валов роторов электрических машин, где δв – воздушный

зазор.

Допускаемые углы поворота:

[θ ] = 0,005 рад (0,3 ) – для шарикоподшипников радиальных;

[θ ] = 0,0025 рад (0,15) – для роликоподшипников радиальных;

[θ ] = 0,05 рад (2…3) – для шарикоподшипников сферических;

[θ ] = 0,001 рад (0,06) – для подшипников скольжения.

Б) Крутильная жесткость.

При расчёте валов на деформацию кручения определяют угол закручивания

. При недостаточной крутильной жёсткости в конструкции вал-шестерня изменяется угол наклона , что приводит к концентрации нагрузки. В

делительных и отсчётных механизмах упругие перемещения снижают точность измерений и т.д. Перемещение при кручении валов постоянного диаметра определяют по формуле:

Tl[ ]

GI , (23.14)

p

где G – модуль сдвига; для сталей G = 0,8·105 МПа.

Значения допускаемых углов закручивания валов колеблется в широких пределах в зависимости от требований, предъявляемых к механизму. Например, в

приводах следящих систем, делительных механизмах и т.д. допускаемые углы ограничивают секундами и минутами на 1 м длины, а в карданных валах автомобилей допускают несколько градусов на метр. Для трансмиссионных валов механизма передвижения мостовых кранов рекомендуется [] = (4…6)10-3 рад/м = (0,25…0,35 град/м).

Малое значение допускаемых перемещений иногда приводит к тому, что размеры вала определяет не прочность, а жёсткость. В этих случаях

нецелесообразно изготовлять вал из дорогих высокопрочных сталей. Так, анализ формул (23.12)…(23.14) показывает, что величины упругих перемещений (δ, θ, )

уменьшаются с увеличением диаметров и моментов инерции I, Ip, которые растут с уменьшением прочности материала.

Пример 23.4. Выполнить проверку на крутильную жёсткость вала:

крутящий момент на валу: Т1 = 161,9 Н·м, диаметр хвостовика dх = 25 мм, [ ] =

0,25 град/м.

Решение.

Назначаем длину хвостовика lх = 1,5dх = 1,5·25 = 37,5 мм. Принимаем lх = 40

мм. Назначаем длину скручивания 0,5lх = 0,5·40 = 20 мм. Полярный момент инерции Iр = π d х4 /32 = π·254/32 = 9287 мм4. Угол закручивания – формула (23.14):

0,8109287

Вывод. Крутильная жёсткость достаточна.

23.8. Расчёт на виброустойчивость

Колебания валов с расположенными на них деталями и узлами возникают при действии внешних постоянно действующих и периодически изменяющихся сил и связаны с упругой деформацией валов. Малые колебания около положения равновесия становятся опасными для вала и конструкции в целом, когда частота возмущающей силы достигает частоты собственных колебаний системы, то есть когда наступает резонанс. При этом напряжения в сечениях вала существенно возрастают и определяются, в основном, не внешней нагрузкой, а силами инерции колеблющихся масс.

Резонанс представляет собой большую опасность для прочности конструкций и его следует избегать. Наиболее часто его предотвращают за счёт изменения частоты собственных колебаний, реже – за счёт изменения частоты возмущающей силы.

Одна из основных задач расчета конструкции на колебания (на виброустойчивость) состоит в определении частот собственных колебаний и

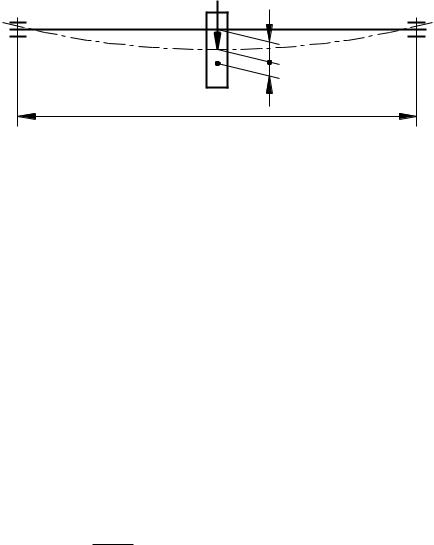
установлении допустимой угловой скорости, ограничиваемой частотой собственных колебаний. Изгибные колебания валов связаны с их изгибной деформацией. На рис. 23.8 приведена схема вала с закреплённым на нём зубчатым колесом, который рассматривают как балку с сосредоточенной массой,

шарнирно закрепленную в жёстких опорах.

Вращающиеся детали не могут быть идеально сбалансированы из-за неизбежных погрешностей технологического характера. Поэтому на практике всегда возникают инерционные силы от дебаланса е, которые уводят вращающиеся на валу детали от оси вращения. При определенной угловой скорости дебаланс вызывает сильную «раскачку» системы. Угловую скорость,

при которой наступает равенство центробежных сил и сил упругости, называют критической. Центробежная сила:

где λ – податливость в мм/Н, то есть деформация, вызываемая единичной силой:

Приравнивая правые части уравнений (23.15) и (23.16), получают:

δ

mω(δe), откуда