Лекции по ТВ и МС(ч.1)

Доказательство. Доказательство проведем методом математической индукции.

Пусть n = 2. Не трудно видеть, что

A1 U A2 = (A1 \ A1 I A2 )U(A2 \ A1 I A2 )U(A1 I A2 ),

Предположим, что формула верна для n −1 события:

числа 1,2,K,n . Карточки расположены в «абсолютно случайном порядке». Какова

49

Аксиомы теории вероятностей Лекция № 5

вероятность того, что хотя бы одно из чисел окажется на месте с таким же номером?

Для любого конечного или счетного числа случайных событий

{An } справедливы неравенства:

Теорема 5.4.

Доказательство. Введем в рассмотрение множества:

B1 = A1 , B2 = A1 I A2 , B3 = A1 I A2 I A3 ,…, Bn = A1 I A2 I A3 IKI An−1 I An .

События Bn попарно несовместны и Bn An . Поэтому

P Un An = P Un Bn = ∑n P(Bn )≤ ∑n P(An ).

Справедливость второго неравенства теоремы следует из следующих рассуждений:

50

P In An =1− P In An =1− P Un An ≥1− ∑n P(An ).

5.4. Рекомендуется изучить самостоятельно:

¾[2] – стр. 33-41;

¾[3] – стр. 38-45,49-54;

¾[4] – стр. 143-151;

¾[5] – стр. 16-18.

5.5. Теоретические вопросы, выносимые на экзамен:

1.Геометрические вероятности. Примеры применения геометрического определения вероятности события.

2.Аксиоматическое построение теории вероятностей. Свойства вероятности.

5.6. В результате успешного усвоения материала лекции студент должен знать:

9понятия:

¾геометрической вероятности;

¾аксиом теории вероятностей;

9теоремы:

¾свойства вероятности;

уметь:

9доказывать теоремы:

¾о вероятности противоположного события;

¾о вероятности разности событий;

¾о сложении вероятностей;

¾об оценках для вероятности суммы и произведения событий;

9решать задачи используя, геометрическое определение вероятностей.

51

Аксиомы теории вероятностей Лекция № 5

5.7. Задачи и упражнения.

1.На отрезок [0;1] случайным образом бросается точка. Найти вероятности следующих событий:

а) длина меньшей части меньше x ; б) длина большей части меньше x ;

в) длины обеих частей одновременно меньше x .

2.Точку A на удачу бросают в квадрат со стороной 1. Найти вероятности того, что:

а) расстояние от точки A до фиксированной стороны квадрата не превосходит x ;

б) расстояние от точки A до ближайшей стороны не превосходит x ; в) расстояние от точки A до центра квадрата не превосходит x ;

г) расстояние от точки A до ближайшей вершины квадрата не превосходит x .

3.Точку B на удачу бросают в прямоугольник со сторонами 1 и 2. Найти вероятности того, что:

а) расстояние от точки B до ближайшей стороны прямоугольника не превосходит x ;

б) расстояние от точки B до любой стороны прямоугольника не превосходит x ;

в) расстояние от точки B до диагоналей прямоугольника не превосходит x .

4.Стержень длиной l случайным образом ломают на три части. Какова вероятность, что из получившихся частей можно составить треугольник?

5.Стержень длиной l случайным образом ломают на три части. Какова вероятность, что длина меньшей части не превышает l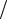3?

6.Какова вероятность, что из трех отрезков, длины которых выбраны наудачу из отрезка [0;l], можно составить треугольник?

7.(Парадокс Бертрана) В круге радиуса R наудачу выбирается хорда. Какова вероятность того, что ее длина не превзойдет длины стороны вписанного в

52

этот круг треугольника?

8. В интервале времени [0;T ] в случайный момент u появляется сигнал длительностью s . Приемник включается в случайный момент времени v [0;T ]

на время t . Предположив, что точка (u;v) равномерно расположена в квадрате

[0;T ]×[0;T ], найти вероятность обнаружения сигнала.

9.На паркет, составленный из правильных k –угольников со стороной a , бросается монета радиуса r . Найти вероятность того, что упавшая монета не заденет границу ни одного из k –угольников паркета для:

а) k = 3 ; б) k = 4 ; в) k = 6 .

9.На окружности радиуса R наудачу взяты три точки A , B , C . Какова вероятность того, что треугольник ABC остроугольный?

10.Какой толщины должна быть монета, чтобы вероятность падения на ребро была равна 13?

11. Определить вероятность того, что корни квадратного уравнения

y = x2 + 2ax +b = 0

а) вещественны; б) положительны;

если равновозможны значения коэффициентов в прямоугольнике a ≤ n , b ≤ m . 12. К автобусной остановке через каждые четыре минуты подходит автобус

линии А, а через каждые шесть минут — автобус линии В. Интервал времени между моментами прихода автобуса линии А и ближайшего следующего автобуса линии В равновозможен в пределах от нуля до четырех минут.

Определить вероятность того, что:

а) первый подошедший автобус окажется линии А; б) автобус какой–либо линии подойдет в течение двух минут.

53

Лекция № 6

1)P(A / B)≥ 0 ;

2)P(Ω/ B)=1;

3)если {Ai }i∞=1 — последовательность попарно несовместных случайных

54

P(B / A)= P(PA(IA)B) или соответственно P(A IB)= P(A)P(B A).

Формулы (6.2) легко допускают обобщение на пересечение любого конечного количества множеств. Пусть A1, A2 ,K, An — случайные события такие,

что

n−1 n−2

Поскольку IAi IAi K A1 I A2 A1 , то из неравенства (6.3) следует, что

что сумма выпавших на них очков равна 8 (событие А), если известно, что сумма есть четное число (событие В)?

Решение: Пространство элементарных исходов для данного эксперимента

55

произойти при выполнении одной из n гипотез, причем вероятности наступлений гипотез известны, требуется найти вероятность события A . Ответ на этот вопрос дает следующая теорема.

Пусть (Ω,F, P) — вероятностное пространство. Набор случайных событий H1,K, Hn , Hi F, i =1,n , образует полную группу событий, если выполнены соотношения

1)H1 U H2 UKU Hn = Ω,

2)Hi I H j = ,(i ≠ j).

Пусть (Ω,F, P) — вероятностное пространство. H1,K, Hn , Hi F, i =1,n — полная группа событий и P(Hi )> 0 , i =1,n , то для любого случайного события A F имеет место равенство

n

P(A)= ∑P(Hi )P(AHi ).

i =1

Так как события Hi , i =1,n попарно несовместны, то такими же будут и события

A I Hi , i =1,n . Поэтому

подходят за билетами один за другим. У кого больше шансов взять «счастливый » билет: у того, кто подошел первым, или у того, кто подошел вторым?

56

«счастливый» билет, H1 — первый студент взял «счастливый» билет, H2 —

первый студент взял «несчастливый» билет. По формуле полной вероятности имеем

P(A)= P(H1 )P(AH1 )+ P(H2 )P(AH2 )= Nn Nn −−11 + NN− n Nn−1 = Nn .

Таким образом, вероятность взять счастливый билет для обоих студентов одна и та же.

Пример 6.3. (задача о разорении игрока). Два игрока А и В продолжают некоторую игру до полного разорения одного из них. Капитал первого равняется a гр., капитал второго — b гр. Вероятность выигрыша каждой партии для игрока А равна p , а для игрока В равна q ; p + q =1 (ничьи отсутствуют). В каждой партии

выигрыш одного игрока (и, значит, проигрыш второго) равняется 1 гривне. Найти вероятность разорения каждого из игроков.

поскольку в первом случае игрок А уже сосредоточил в своих руках весь капитал, а во втором он уже ничего не имеет.

Если игрок А имел n гр. перед некоторой партией, то его разорение может осуществиться двумя различными способами: или он очередную партию выиграет, а всю игру проиграет, или он проиграет и партию и игру. По формуле полной вероятности имеем

pn = p pn+1 + q pn−1 .

Относительно pn мы получили уравнение в конечных разностях; легко видеть, что его можно записать в

Рассмотрим сначала решение этого уравнения при p = q =12 . При этом допущении pn+1 − pn = pn − pn−1 =K= p1 − p0 = c ,

где c — постоянная. Отсюда находим, что pn = p0 + nc . Поскольку справедливы равенства (6.4), то pn =1− a +n b .

Таким образом, вероятность разорения игрока А равняется

pa =1− a a+ b = a b+ b .

Аналогично в случае p = q =12 вероятность разорения игрока В

qb = a +a b .

В общем случае при p ≠ q из (6.5) находим, что

После выполнению упрощений и с учетом соотношений (6.4) получим, что pn − pn−1 = (q p)n (p1 −1).

Рассмотрим разность pn+1 − pn = (q p)n (p1 −1), очевидно, что

Поскольку pa+b = 0 , то

57

pn = (1− p1 )(q p1)n−−q(qpp)a+b

а так как p0 =1, то

1 = (1− p1 )(q p1)0−−q(qpp)a+b .

Из двух последних равенств получаем, что

Аналогично в случае p ≠ q получаем, что вероятность разорения игрока В равна

6.3. Формулы Байеса

Доказательство. Используя определение условной вероятности, теорему умножения вероятностей и формулу полной вероятности, имеем:

Общая схема применения этих формул при решении практических задач следующая. Пусть событие B может происходить в различных условиях, о характере которых можно выдвинуть n гипотез H1,K, Hn . Из каких–то соображений известны вероятности этих гипотез P(H1 ),K, P(Hn ) (их так же называют априорными вероятностями). Известны также условные вероятности P(BH1 ),K, P(BHn ). Предположим, что произведен опыт, в результате которого

58