Лекции по ТВ и МС(ч.1)

9.1. Определение случайной величины

Пусть (Ω,F, P) — вероятностное пространство. Всякая

89

Следовательно, введённая таким образом функция ξ(ω) является случайной величиной. Функция распределения для этой случайной величины имеет вид:

1/2

Пример 9.2. Пусть (Ω,F, P) — произвольное вероятностное пространство.

Предположим, что A — некоторое случайное событие (A F) и

( ) 1, ω A,

χA ω = 0, ω A.

Тогда

, x ≤ 0, {ω : χA (ω)< x}= A, 0 < x ≤1,

Ω, x >1.

Следовательно, множество {ω : χA (ω)< x} F.

Таким образом χA (ω) — случайная величина с функцией распределения следующего вида:

90

неизмеримое по Лебегу множество из отрезка [0;1]. Рассмотрим функцию:

множеств принадлежит σ –алгебре F.

Доказательство. Поскольку F суть σ –алгебра и при каждом действительном x

{ω : ξ(ω)< x} F, то каждое из множеств

{ω : ξ(ω)≥ x}= Ω{ω : ξ(ω)< x}

{ω : ξ(ω)> x}= Ω{ω : ξ(ω)≤ x}

{ω : ξ(ω)= x}={ω :ξ(ω)≤ x}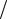{ω : ξ(ω)< x} {ω : a ≤ξ(ω)< b}= {ω : ξ(ω)< b}{ω :ξ(ω)< a} {ω : a <ξ(ω)< b}= {ω : ξ(ω)< b}{ω :ξ(ω)≤ a}

91

принадлежит F.

Пусть (Ω,F, P) — вероятностное пространство, а ξ(ω), η(ω)

Доказательство. Пусть Q ={rk } — множество всех рациональных чисел. Тогда

{ω : ξ(ω)<η(ω)}= U{ω :ξ(ω)< rk <η(ω)}.

rk

Поскольку

{ω : ξ(ω)< rk <η(ω)}={ω : ξ(ω)< rk }I{ω : rk <η(ω)},

то

{ω : ξ(ω)<η(ω)} F.

В предыдущем рассуждении ξ(ω) и η(ω) входят совершенно равноправно,

поэтому {ω : ξ(ω)>η(ω)} F.

Таким образом,

{ω : ξ(ω)≤η(ω)}= Ω{ω : ξ(ω)>η(ω)} F.

И, наконец,

{ω : ξ(ω)=η(ω)}={ω : ξ(ω)≥η(ω)}I{ω : ξ(ω)≤η(ω)} F.

Следствием теорем 9.1 и 9.2 является следующее утверждение:

Пусть (Ω,F, P) — вероятностное пространство, а ξ(ω), η(ω)

случайные величины на нём. Тогда

Остальные случаи доказать самостоятельно.

92

Функция f (x): Rm → R1 , измеримая относительно σ –алгебры

Определение 9 .4 борелевских множеств в Rm , называется борелевской

функцией.

В теории вероятностей часто рассматриваются функции от случайных величин. При этом, естественным образом, возникает вопрос, являются ли эти функции случайными величинами. Ответ на этот вопрос дает следующая теорема,

93

ξ1(ω),ξ2 (ω),K,ξm (ω) — случайные величины на вероятностном

Теорема 9.5.

пространстве (Ω,F, P). Тогда f (ξ1(ω),ξ2 (ω),K,ξm (ω)) — случайная величина.

Доказательство можно найти в [2, стр.56].

9.3. Дискретные случайные величины.

Пусть (Ω,F, P) — вероятностное пространство. Случайная Определение 9 .5 величина ξ(ω) называется дискретной случайной величиной,

если она принимает конечное или счетное число значений.

Пусть (Ω,F, P) — вероятностное пространство и

ξ =ξ(ω): Ω → R1 — функция, принимающая конечное или счетное число значений x1, x2 ,K, xn ,K Функция ξ(ω) измерима относительно F тогда и только тогда, когда для каждого n

{ω : ξ(ω)= xn } F.

Доказательство.

Необходимость следует из теоремы 1 настоящей лекции. Достаточность следует из соотношения

{ω : ξ(ω)< x}= U{ω :ξ(ω)= xi } F ,

i:xi <x

которое выполнено для каждого x .

Итак, мы имеем, что если ξ(ω) — дискретная случайная величина на вероятностном пространстве (Ω,F, P), принимающая значения x1, x2 ,K, xn ,K, то

94

9.4. Некоторые дискретные распределения

9.4.1. Биномиальное распределение

Случайная величина ξ(ω) называется биномиальной, если pr = P{ω :ξ(ω)= r}= Cnk pk (1− p)n−k , k = 0, n, 0 ≤ 0 ≤1.

Итак, значение биномиальной случайной величины равно количеству успехов в серии из n испытаний Бернулли.

9.4.2. Геометрическое распределение

Предположим, что производятся независимые испытания, причем, при каждом испытании может быть два исхода — успех (У) с вероятностью p и

неудача (Н) с вероятностью q =1− p . Пусть испытания проводятся до первого появления успеха. Обозначим через ξ — число испытаний, предшествующих первому появлению успеха. В качестве пространства элементарных событий можно рассматривать множество

95

Набор вероятностей (9.2) называется геометрическим распределением.

Интересно отметить, что геометрическое распределение единственное из дискретных распределений, которое обладает свойством отсутствия последействия, т.е.

Полагая n =1 в равенстве (9.4), имеем

9.4.3. Отрицательное биномиальное распределение

Предположим, что производятся независимые испытания, в каждом из которых появляется успех с вероятностью p, неудача с вероятностью q = p −1.

Пусть случайная величина ξ равна номеру испытания, в котором произошел r –й

успех. Тогда

96

Замечание 9.1. Альтернативный вид отрицательного биномиального распределения:

P{ξ = m}= Cr −−1 pr qm−r , n = r, r +1,K

m 1

Замечание 9.2. Отрицательное биномиальное потому, что

Распределение находит применение в теории случайных процессов, теории риска, теории массового обслуживания, теории надёжности.

9.5. Рекомендуется изучить самостоятельно:

¾[2] – стр. 49 — 63;

¾[3] – стр. 116 — 123.

9.6. Теоретические вопросы выносимые на экзамен:

1.Определение случайной величины. Случайные события, порожденные случайной величиной.

2.Дискретные случайные величины: биномиальная, геометрическая, отрицательно биномиальная, пуассоновская.

97

Дискретные случайные величины Лекция № 9

9.7. В результате успешного усвоения материала лекции студент должен знать:

9определения:

¾случайной величины;

¾функции распределения случайной величины;

¾дискретной случайной величины;

¾индикатора случайного события;

¾борелевской функции;

¾биномиальной случайной величины;

¾отрицательной биномиальной случайной величины;

¾геометрической случайной величины;

9теоремы:

¾о случайных событиях, порожденных случайной величиной;

¾о случайных событиях, порожденных двумя случайными величинами;

¾об арифметических операциях над случайными величинами;

¾о функциях от случайных величин;

уметь:

9доказывать теоремы:

¾о случайных событиях, порожденных случайной величиной;

¾о случайных событиях, порожденных двумя случайными величинами;

¾об арифметических операциях над случайными величинами.

9.8. Задачи и упражнения

1. На пути следования автомобиля расположены 5 светофоров. Каждый из которых с вероятностью 0,6 разрешает движение и с вероятностью 0,4 запрещает его. Пусть случайная величина ξ равна количеству светофоров, которые проехал автомобиль до первой остановки. Найти распределение ξ .

2. Опыт состоит в трехкратном подбрасывании симметричной игральной кости. Случайная величина η равна количеству появлений пяти очков на верхней грани. Найти распределение случайной величины η.

98