
Binder1
.pdf
при k 0 : 3 2 |
cos |
|
isin |
|
|
; при k |
1: |
|
|
3 2 |
cos13 |
isin |
13 |
; |
|||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|||||||||
при k 2 : |
|
3 2 cos 25 isin |
25 |
3 |
2 cos 11 |
isin |
11 |
. |
|
||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
18 |
|
|
|
|||||
Пример 6. Вычислить |
1 i |
3 12 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2i 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. Запишем числа 1 i |
3 и |
2 2i |
|
в тригонометрической форме: |
|||||||||||||||||||||||||||||||||||
1 i 3 |
2 |
|
|
|
|
isin |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
cos |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 2i |
8 cos |
|
|
|
isin |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Применяя формулу Муавра, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
12 |
|
12 |
|
|
12 |
isin |
12 |
12 |
|
|
|
|
|
|
12 |
|
|
|
12 |
||||||||||||||||||||
1 i 3 |
|
2 |
|
cos |
|
3 |
|
|
3 |
|
2 |
|
cos4 isin 4 2 |
cos0 isin 0 2 , |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
8 |
|
|
|
|
8 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
12 |
|
|
|
|
|
|
|
|
|
|
||
2 2i |
|
8 |
|
cos |
|
|
|
|
|
isin |
|
|
|
|
|
2 |
cos 2 isin 2 |
|
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
212 cos0 isin 0 212. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Откуда 1 i |
|
3 12 |
212 |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 2i 8 |
|
|
212 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Представим это число в показательной форме |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
1 i 3 2ei 3 , 1 i |
|
3 12 212 ei123 |
212 ei4 212 ; |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
2 2i |
8e i 4 , |
2 2i 8 212 |
e i2 |
212 , так как cos 2 k isin 2 k 1, |
k Z . |
||||||||||||||||||||||||||||||||||
1 i 3 12 |
|
212 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 2i 8 |
|
212 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 7. Решить уравнение z2 6z 10 0. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Решение. z1,2 3 |
9 10 |
3 i, т.е. z1 |
3 i, z2 3 i. |
|
|
|
|||||||||||||||||||||||||||||||||
Ответ: 3 i; 3 i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Пример 8. Решить уравнение z2 2i 3 z 5 i 0. |
|
|||||||||
|
|
|
|
Решение. По формуле корней квадратного уравнения |
|
|||||||||
Z |
3 2i 3 2i 2 4 5 i |
|
3 2i 9 12i 4 20 4i 3 2i 15 8i |
|||||||||||
|
|
|||||||||||||
1,2 |
|
|
2 |
|
|
|
|
|
2 |
2 |
||||
|
3 2i 1 4i |
, т.к. |
15 8i |
1 4i 2 . |
|
|
|
|||||||
|
|
|
|
|||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Отсюда z 3 2i 1 4i 1 i, z |
2 |
3 2i 1 4i |
|
2 3i. |
|
|||||||||
|
|
|
1 |
2 |
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Ответ. 1 i;2 3i . |
|
|
|
|
|
|
|
|
||
|
|
Пример 9. Решить биквадратное уравнение z4 4z2 3 0. |
|
|||||||||||
|
|
|
|
Решение. Обозначим z2 t, тогда t2 4t 3 0, корни которого t |
3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
и t |
2 |
1, т.е. |
z2 3 z |
i 3, z |
2 1 z |
|
i. |
|
||||||
|
|
|
|
1,2 |
|
|
|
|
3,4 |
|
|
|||
Ответ: i, 3i .
Пример 10. Найти а) i9 , б) i42 , в) i19 , г) i28 . Решение.
а) i9 i8 1 i4 2 i 1 i i;
б) i42 i40 2 i4 10 i2 1 1 1;
в) i19 i16 3 i3 i;
г) i28 i4 7 17 1.
|
|
|
|
|
Задачи для самостоятельной работы |
|
|
|
Выполнить указанные действия: |
||
11. |
3 2i 5 i . |
Ответ: 8 i . |
|||
12. |
1 3i 2 i . |
Ответ: 3 2i . |
|||
13. |
5 i 2 3i . |
Ответ: 13 13i . |
|||
14. |
1 |
i |
. |
Ответ: i . |
|
|
1 |
|
|||
|
i |
|
|||
26

15. |
|
|
1 |
|
|
1 |
. |
Ответ: |
0,4 i 0,2 . |
|||
1 |
3i |
3 i |
||||||||||
|
|
|
|
|
|
|
||||||
16. |
3 2i 3 . |
|
Ответ: |
9 46i . |
||||||||
17. |
i5 2i2 |
2 |
|
Ответ: |
2 |
3 |
i . |
|||||
|
19 |
1 |
. |
|
2 |
|||||||
|
|
i |
|
|
|
|
|
|||||
18. |
3 2i 1 i3 |
|
4 i 2 3i |
. |
Ответ: 7,3 i 0,1. |
|
||||
1 i |
|
|
3 i |
|
||||||
|
|
|
|
|
|
|
|
|||
19. |
i28 5i13 i9 |
i2 |
4 . |
|
|
Ответ: 6 4i . |
|
|||
20. |
Найти Rez и Imz , если: |
|
|
|
|
|||||
|
а) z 3 2i |
, б) z |
2 3i |
, в) z |
4 i . |
|
||||
|
3 i |
|
||||||||
|
1 i |
|
|
|
|
|
|
1 2i |
|
|
|
Ответы: а) Rez 0,5; |
Imz 2,5; |
|
|
||||||
|
|
б) Re z 0,9; Im z 0,7; |
|
|||||||
|
|
в) Rez 1,2; Imz 1,4 . |
|
|||||||
|
Найти модуль и главное значение аргумента: |
|
||||||||
21. |
z 2 3 2i . |
|
|
|
|
|
|
Ответ: r 4, |
. |
|
|
|
|
|
|
|
|
|
|
|
6 |
22. |
z 1 i 3 . |
|
|
|
|
|
|
|
Ответ: r 2, . |
|
|
|
|
|
|
|
|
|
|
3 |
|
23. |
5 7i 7 5i . |
|
|
|
|
Ответ: r 74, |
. |
|||
|
|
|
|
|
|
|
|
|
|
2 |
24. |
1 i 3 3 . |
|
|
|
|
|
|
|
Ответ: r 8, . |
|
Следующие комплексные числа представить в тригонометрической и показательной формах:
25. |
z |
2 i 2 . |
Ответ: z 2 |
|
|
|
|
|
|
|
|
|
2e |
|
i |
. |
|||
cos |
|
|
isin |
|
|
4 |
|||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
||
26. |
z |
3 i . |
Ответ: z 2 |
|
5 |
isin |
5 |
2e |
i |
5 |
|
|
|
|
|||||
|
|
|
|
||||||||||||||||
cos |
|
6 |
6 |
|
|
|
6 . |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
27
|
|
|
|
|
|
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
||||||||
27. |
|
z |
|
|
|
|
|
i |
|
|
. |
|
|
Ответ: z 1 cos |
|
|
isin |
|
|
|
e 3 . |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
Вычислить: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
28. |
|
1 i |
8 |
|
|
|
|
|
|
|
Ответ: 1. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
1 |
i |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
29. |
|
|
|
|
3 i 6 . |
|
|
|
|
|
Ответ: 64 . |
|
|
|
|
|
|
|
|
||||||||||||||||||
30. |
|
|
|
|
cos |
|
isin |
6 |
Ответ: 27 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1 |
3 |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
31. |
3 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: 1; |
1 i |
3 . |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
32. |
|
3 i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: i; |
|
|
3 |
|
i |
. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
33. |
|
|
3 4i . |
|
|
|
|
|
Ответ: |
2 i . |
|
|
|
||||||||||||||||||||||||
34. |
|
|
2 i2 3 . |
|
|
|
|
Ответ: |
3 i . |
|
|
|
|||||||||||||||||||||||||
35. |
|
6 8 . |
|
|
|
|
|
|
|
Ответ: |
|
|
2 |
|
3 i ; 2i; |
|
2 |
|
3 i . |
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Построить области точек z , удовлетворяющих условиям (36-40): |
|
|
|
|||||||||||||||||||||||||||||
36. |
|
z 1 |
|
|
2. |
Ответ. Окружность с центром в точке С (1; 0) и радиусом 2. |
|
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
37. |
Rez 1. |
|
|
|
|
|
|
|
Ответ. Прямая x 1. |
|
|
|
|||||||||||||||||||||||||
38. |
|
z |
|
|
2 |
и 0 arg z . |
Ответ. Часть круга с центром в начале |
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
координат и радиусом 2, |
расположенная в 1 четверти. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
39. |
0 Imz 1. |
|
|
|
|
Ответ. Полоса 0 y 1. |
|
|
|
||||||||||||||||||||||||||||
40. |
|
z i |
|
|
|
z 2 |
|
. |
|
Ответ. |
Прямая 2x y 1,5 0. |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Решить следующие уравнения (41-46): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
41. |
|
z2 2z 5 0 . |
|
Ответ: 1 2i . |
|
|
|
||||||||||||||||||||||||||||||
28
42. |
4z2 2z 1 0 . |
Ответ: 1 |
|
|
3 |
i . |
|||
|
4 |
||||||||
|
|
4 |
|
|
|
|
|
||
43. |
z2 2i 3 z 5 i 0 . |
Ответ: 1 i; 2 3i . |
|||||||
44. |
z3 1 0 . |
Ответ: 1; |
1 |
|
i |
3 |
. |
||
2 |
|
|
|||||||
|
|
|
|
2 |
|
||||
45. |
z 1 4 16 0 . |
Ответ: 1; 3; 1 2i . |
|||||||
46. |
z4 9z2 20 0 . |
Ответ: 2i; |
|
5i . |
|||||
47. Используя тождество cos isin n cos n isin n , выразить sin3 и
cos3 |
через функции угла . Ответ: |
sin3 3sin 4sin3 |
, |
|
cos3 4cos3 3cos |
||||
|
|
|||
§ 4. Некоторые сведения о многочленах
Многочленом n - ой степени или целой рациональной функцией называется выражение вида
P x |
a xn a xn 1 ... a |
n 1 |
x a |
n |
, |
|
n |
0 |
1 |
|
|
||
где n - целое положительное число. |
|
|
||||
Здесь |
коэффициенты |
a0 ,a1 ,...,an являются действительными или |
||||
комплексными числами, независимая переменная x может принимать действительные и комплексные значения.
Корнем многочлена |
P x называется всякое число (действительное или |
комплексное), при котором многочлен обращается в нуль, т.е. P 0 . |
|
Теорема Безу. При делении многочлена P x на двучлен x a получается |
|
остаток, равный P a . |
|
Следствие. Если - корень многочлена Pn x , то этот многочлен делится |
|
без остатка на x и, |
следовательно, представляется в виде произведения |
Pn x x Pn 1 x , где Pn 1 x - многочлен степени n 1 .
Основная теорема алгебры. Всякий многочлен с любыми числовыми коэффициентами, степень которого не меньше единицы, имеет хотя бы один корень, в общем случае комплексный.
29

Следствие. Всякий многочлен может быть представлен в виде следующего
произведения |
|
Pn x a0 x 1 x 2 ... x n , |
(1) |
где a - коэффициент при xn , |
|
0 |
|
1, 2 ,..., n - корни многочлена Pn x . |
|
Если множитель x в этом разложении встречается |
k раз, то корень |
называется корнем кратности k . При k 1 этот корень называется простым. Если многочлен с действительными коэффициентами имеет комплексный
корень i кратности |
k , |
то сопряженное число i также является |
||||||||||||||||||||||||
корнем этого многочлена причем той же кратности |
k . Отсюда вытекает, что в |
|||||||||||||||||||||||||
разложении (1) многочлена |
P |
x |
|
|
будут присутствовать множители x k и |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
x |
|
k . Перемножив их, получим |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x k |
|
x |
|
|
k x |
|
x |
|
|
k |
|
x |
i x |
i k |
||||||||||
|
|
|
2 |
|
|
|
|
|
|
2 |
|
2 |
|
k |
|
|
|
2 |
|
|
|
|
k |
|
|
|
|
|
|
2 x |
|
|
|
x |
|
px q , |
|
|
|||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
где p 2 , |
q 2 2 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Таким |
образом, |
разложение |
(1) |
многочлена |
Pn x с |
действительными |
||||||||||||||||||
коэффициентами перепишется
Pn x a0 x x1 k1 x x2 k2 ... x2 p1x q1 m1 ... x2 ps x qs ms ,
где k1 k2 ... 2m1 ... 2ms n , что дает возможность избежать комплексных чисел при разложении многочлена с действительными коэффициентами на множители.
Дробно-рациональной функцией или рациональной дробью называется отношение двух многочленов:
R x Pn x , Qm x
где Pn x - многочлен степени n , а Qm x - многочлен степени m .
30
Если n m , то рациональная дробь R x называется правильной, в противном случае, т.е. когда n m , рациональная дробь называется неправильной.
Всякая неправильная рациональная дробь может быть записана как сумма
многочлена и правильной рациональной дроби, т.е. R x |
P x |
L x |
r x |
, |
||
Q x |
Q x |
|||||
|
|
|
|
|||
где L x - частное, а r x - остаток, получаемые при делении многочлена P x |
на |
|||||
многочлен Q x . |
|
|
|
|
|
|
Деление многочленов столбиком. Алгоритм деления многочлена Pn x |
на |
|||||
многочлен Qm x |
при n m является обобщенной формой |
деления чисел |
||||
столбиком. |
|
|
|
|
|
|
|
|
|
||||
Покажем, что |
x3 4x2 5x 1 |
x2 |
x 8 |
25 |
. |
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
x 3 |
|
x 3 |
|
|
|
||||
Частное и остаток от деления |
P x x3 4x2 5x 1 на |
Q x x 3 |
|||||||||||
находим, выполняя следующие шаги: |
|
|
|
|
|
|
|||||||
1) Делим старший член делимого на старший член делителя, т.е. |
x3 |
x2 , и |
|||||||||||
x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
результат записываем в частном под чертой |
|
|
|
|
|
||||||||
|
x 3 |
|
|
|
|
|
|
|
|
||||
x3 4x2 5x 1 |
|
|
. |
|
|
|
|
|
|
|
|||
|
|
|
|
x2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
2) Умножаем полученный результат x2 |
на делитель и записываем под |
||||||||||||
делимым |
|
|
|
|
|
|
|
|
|
||||
x3 4x2 5x 1 |
|
|
x 3 |
. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||
x3 3x2 |
|
|
x2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
3) Из делимого вычитаем многочлен, полученный умножением x2 на x 3, |
|||||||||||||
x3 4x2 5x 1 x3 3x2 x3 4x2 5x 1 x3 3x2 x2 5x 1 |
и |
||||||||||||
записываем этот результат под чертой
31
x3 4x2 5x 1 |
|
|
x 3 |
. |
|
||||
x3 3x2 |
|
|
x2 |
|
|
|
|
x2 5x 1
4) Повторяем первые три шага, но при этом в качестве делимого рассматриваем многочлен, записанный под чертой
x3 4x2 5x 1 |
|
|
x 3 |
|
|
||||
|
|
|
|
. |
x3 3x2 |
|
|
x2 x |
|
x2 5x 1
x2 3x
8x 1
5)Повторяем четвертый шаг до тех пор, пока не получим многочлен, степень которого меньше степени делителя
x3 4x2 5x 1
x3 3x2
x2 5x 1
x2 3x
8x 1
8x 24
25
Получим частное
x 3
x2 x 8 .
L x x2 x 8 и остаток r x 25 . Итак,
|
x3 4x2 5x 1 |
x2 |
x 8 |
|
25 |
. |
|
|
|
||||
|
x 3 |
|
|
x 3 |
||
|
|
|
Примеры решения задач |
|||
Пример 1. Найти корни многочлена z4 4 и разложить его на линейные и |
||||||
квадратичные множители. |
|
|
|
|
||
Решение. Найдем корни |
многочлена, приравнивая его к нулю z4 4 0. |
|||||
Отсюда, z4 4 или z 4 |
4 . |
|
|
|
||
|
|
|
|
32 |
||
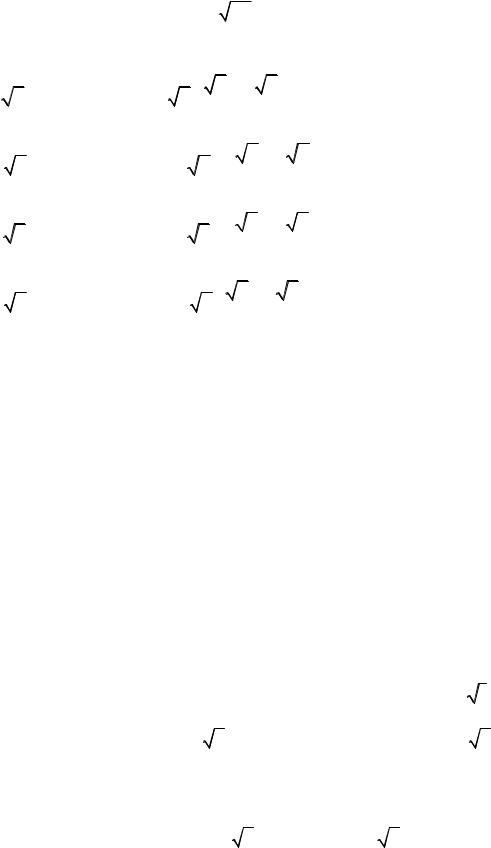
Вычислим все корни |
4 4 . В тригонометрической форме |
4 4 cos isin , тогда (см. гл. 1, §3):
z1 |
4 |
|
|
|
isin |
|
|
|
|
|
|
2 |
|
i |
|
2 |
|
1 i , |
|
||||||||||||||||
4 |
cos |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
4 |
4 |
|
2 |
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
z2 |
4 |
|
|
|
3 |
|
isin |
3 |
|
|
|
|
|
|
|
|
2 |
i |
|
2 |
|
1 |
i , |
||||||||||||
4 |
cos |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
4 |
4 |
|
|
|
2 |
|
|
2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
z3 |
4 |
|
|
5 |
|
isin |
5 |
|
|
|
|
|
|
|
|
2 |
i |
|
|
2 |
|
1 |
i , |
||||||||||||
4 |
cos |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
4 |
|
4 |
|
|
|
2 |
|
|
2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
z4 |
4 |
|
|
|
7 |
|
isin |
7 |
|
|
|
|
|
|
|
|
2 |
|
i |
|
|
|
2 |
1 i . |
|||||||||||
4 |
cos |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
4 |
|
4 |
|
|
|
|
2 |
|
|
|
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Запишем разложение многочлена
z4 4 z z1 z z2 z z3 z z4 z 1 i z 1 i z 1 i z 1 i
z 1 i z 1 i z 1 i z 1 i z 1 2 i2 z 1 2 i2
z2 2z 1 1 z2 2z 1 1 z2 2z 2 z2 2z 2 .
Т.к. все корни многочлена комплексные, то разложение его содержит только квадратичные множители.
Ответ: 1 i, |
1 i ; |
z4 4 z2 2z 2 z2 2z 2 . |
Пример 2. Найти корни многочлена z6 2z3 1 и разложить его на множители.
Решение. Так как z6 2z3 1 z3 1 2 , то корнями его будут 3 1 , а именно,
z 1, |
z |
2 |
cos 2 isin 2 |
1 |
i |
|
3 |
, |
z |
cos 4 |
isin 4 |
1 i |
3 |
, имеющие |
||||||||||||
|
|
|
||||||||||||||||||||||||
1 |
|
3 |
3 |
|
|
2 |
|
|
|
2 |
|
|
3 |
|
|
3 |
|
|
|
3 |
|
2 |
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
кратность k 2 .Тогда многочлен перепишется в виде: |
|
|
|
|
|
|
||||||||||||||||||||
|
z6 |
2z3 |
1 z 1 |
2 |
|
|
|
1 |
|
|
|
3 |
|
2 |
|
|
|
1 |
|
3 |
|
2 |
|
|
||
|
|
z |
|
|
|
i |
|
|
|
|
z |
|
|
|
i |
|
. |
|
|
|||||||
|
|
2 |
|
2 |
|
2 |
2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
33
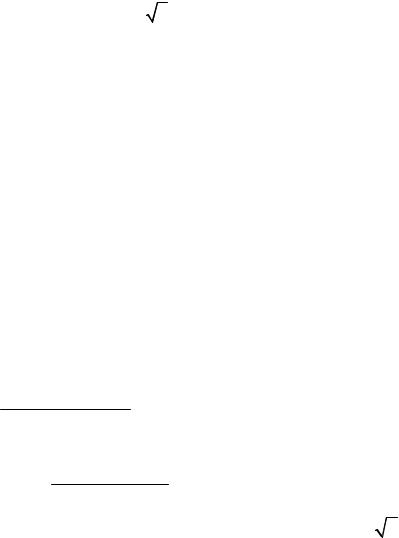
Объединим произведение последних двух множителей и получим z6 2z3 1 z 1 2 z2 z 1 2 . Это разложение содержит как линейный, так и квадратичный множители.
Ответ: 1; |
1 |
i |
3 |
; z 1 2 z2 z 1 2 . |
|
2 |
|||||
|
2 |
|
|
||
Пример 3. Разложить на множители многочлен z4 2z3 4z2 4z 4, если |
|||||
известен один корень z1 1 i . |
|||||
Решение. |
Если |
z1 1 i - корень многочлена, то сопряженное ему число |
|||
z2 1 i также является корнем этого многочлена, т.е. в разложении многочлена будет произведение
z z z z |
2 |
z 1 i z 1 i z 1 2 i2 z2 2z 2 . |
|||
1 |
|
|
|
|
|
А это значит, что оставшиеся множители можно определить путем деления |
|||||
данного многочлена на z2 2z 2 : |
|||||
|
z2 2z 2 |
||||
z4 2z3 4z2 4z 4 |
|
||||
z4 2z3 2z2 |
|
z2 2 |
|
||
2z2 4z 4 2z2 4z 4
0
В частном получили z2 2 . Его корни i 2 - мнимые, которым в разложении многочлена соответствует квадратичный множитель z2 2 . Итак,
z4 2z3 4z2 4z 4 z2 2z 2 z2 2 . |
|
|
|
|
|
Ответ: z2 2z 2 z2 2 . |
|
|
|
|
|
Пример 4. Показать, что 3x4 6x3 5x2 9x 11 |
3x2 |
4 |
x 1 |
. |
|
x2 2x 3 |
|||||
x2 2x 3 |
|
|
|
Решение. Разделим многочлен числителя на многочлен знаменателя столбиком
34
