4.5. Регрессионный анализ

Ниже излагаются основные положения регрессионного анализа, применение которого для обработки результатов наблюдений связано с меньшим числом ограничений, чем корреляционного анализа. Как и корреляционный анализ регрессионный анализ включает в себя построение уравнения регрессии, например методом наименьших квадратов, и статистическую оценку результатов. Если в регрессионном анализе расчет коэффициентов ведется теми же методами, например наименьших квадратов, то теоретические предпосылки регрессионного анализа требуют других способов статистической оценки результатов.

При проведении регрессионного анализа примем следующие допущения:

1. Входной параметр x измеряется с пренебрежимо малой ошибкой. Появление ошибки в определении y объясняется наличием в процессе невыявленных переменных и случайных воздействий, не вошедших в уравнение регрессии.

2. Результаты наблюдений y₁, y₂,..., y_i,..., y_nнад выходной величиной представляют собой независимые нормально распределенные случайные величины.

3. При проведении эксперимента с объемом выборки n при условии, что каждый опыт повторен m* раз, выборочные дисперсии S₁²,..., S_i²,..., S_n²должны быть однородны. При выполнении измерений в различных условиях возникает задача сравнения точности измерений. При этом следует подчеркнуть, что экспериментальные данные можно сравнить только тогда, когда их дисперсии однородны. Это означает, как уже отмечалось (см. п. 3.5.2 и п. 3.5.3), принадлежность экспериментальных данных к одной и той же генеральной совокупности. Напомним, что однородность дисперсий свидетельствует о том, что среди сравниваемых дисперсий нет таких, которые с заданной надежностью превышали бы все остальные, т.е. была бы большая ошибка. При одинаковом числе параллельных опытов однородность дисперсии, как мы уже показали, можно оценить по критерию Кохрена, а для сравнения двух дисперсий целесообразно воспользоваться F-критерием Фишера (см. примеры 3.7–3.9).

После того, как уравнение регрессии найдено, необходимо провести статистический анализ результатов. Этот анализ состоит в следующем: проверяется значимость всех коэффициентов и устанавливается адекватность уравнения.

4.5.1. Проверка адекватности модели

При моделировании приходится формализовать связи исследуемого явления (процесса), из-за чего возможна потеря некоторой информации об объекте. Иногда некоторые связи не учитываются. В то же время основное требование к математической модели заключается в ее пригодности для решения поставленной задачи и адекватности процессу.

Так, построив модель в виде линейного уравнения регрессии, мы хотим в частности убедиться, что никакие другие модели не дадут значительного улучшения в описании предсказания значений Y.

Сформулируем нуль-гипотезу Н₀: "Уравнение регрессии адекватно". Альтернативная гипотеза Н₁: "Уравнение регрессии неадекватно". Для проверки этих гипотез принято использовать F-критерий Фишера.

При этом общую дисперсию (дисперсию выходного параметра) S_y²сравнивают с остаточной дисперсией (дисперсией адекватности) S_yост².

Напомним, что

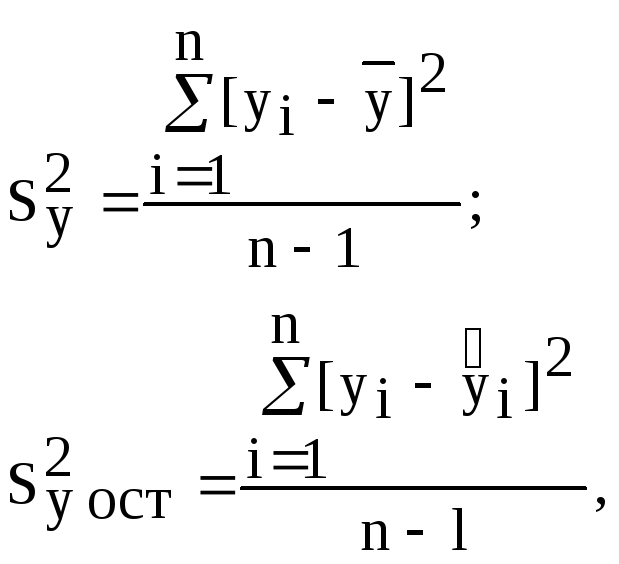(4.24)

где l=k+1 – число членов аппроксимирующего полинома, а k – число факторов. Так, например для линейной зависимости (4.5) k=1, l=2.

В дальнейшем определяется экспериментальное значение F-критерия Фишера

(4.25)

который в данном случае показывает во сколько раз уравнение регрессии предсказывает результаты опытов лучше, чем среднее

Если F_эксп>F_;m1;m2, то уравнение регрессии адекватно. Чем больше значение F_эксппревышает F_;m1;m2для выбранногои числа степеней свободы m₁=n-1, m₂=n-l, тем эффективнее уравнение регрессии.

Рассмотрим так же случай, когда в каждой i-й точке x_iдля повышения надежности и достоверности осуществляется не одно, а m* параллельных измерений (примем для простоты, что m* одинаково для каждого фактора). Тогда число экспериментальных значений величины Y составит n_=nm*.

В этом случае для оценки адекватности модели:

1. Определяется 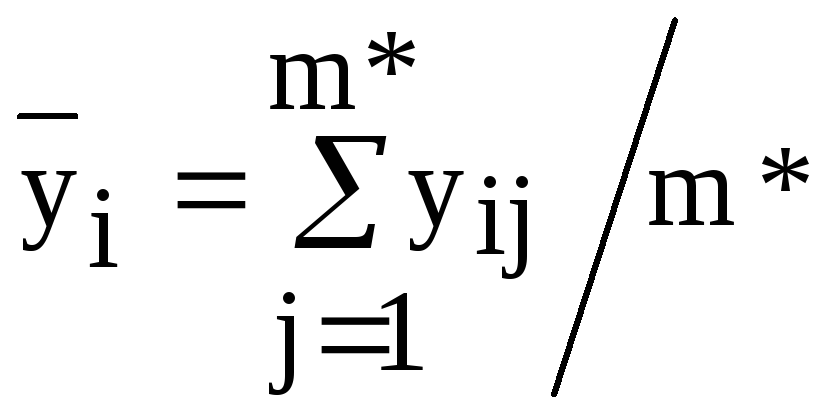– среднее из серии параллельных опытов при x=x_i, где y_ij– значение параметра Y при x=x_iв j-м случае.

2. Рассчитываются значения параметра по уравнению регрессии при x=x_i.

3. Рассчитывается дисперсия адекватности (аналог остаточной дисперсии)

где n – число значений x_i; l – число членов аппроксимирующего полинома (коэффициентов b_i), для линейной зависимости l=2.

4. Определяется выборочная дисперсия Y при x=x_i:

5. Определяется дисперсия воспроизводимости (аналог общей дисперсии)

Число степеней свободы этой дисперсии равно m₁=n(m*-1).

6. Определяется экспериментальное значение критерия Фишера

7. Теоретическое значение этого же критерия F_;m1;m2, где m₁=m*(n-1), m₂=n-l.

8. Если F_экспF_;m1;m2, то уравнение регрессии адекватно, в противном случае – нет.