3.4.2. Оценка доверительного интервала для дисперсии

Для оценки доверительного интервала дисперсии используется ²(читается: "хи-квадрат-критерий"), предложенный английским математиком и биологом К.Пирсоном. Если обозначить через

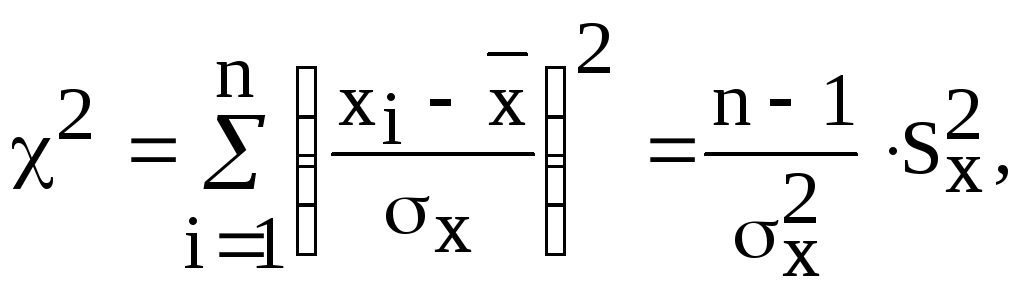(3.22)

то величина ², связанная с дисперсией_x, будет иметь следующий закон распределения:

(3.23)

где m – число степеней свободы этого распределения (m=n-1).

На рис.3.3 приведены кривые f(²) для различных значений m. Эти кривые асимметричны, причем асимметрия особенно резко выражена при малых значениях параметра m. При m=1 кривая уходит в бесконечность при²=0, при m=2 она достигает максимального значения, равного 0,5; при m>2 кривые имеют максимум при²_max=m-2. При больших значениях m² -распределение переходит в нормальное со средним значениеми дисперсией_²=1.

Рис.3.3. Кривые ²-распределения для различных степеней свободы m

Рис.3.4. Определение границ доверительного интервала для оценки дисперсии ²при значении надежности P=1-2₁

Применяя соотношение (3.22), можно записать

где ²=m/², но и после этого величина²остается неизвестной, т.к. значение², входящее в это равенство, а следовательно, и значение коэффициента²остается неизвестным. Тем не менее с помощью²-распределения можно найти границы доверительных интервалов для_x². Для этой цели необходимо определить такие значения₁²(m) и₂²(m), которые выделяют Р – долю площади под соответствующей f(²) кривой (рис.3.4). Эти значения₂²(m) и₁²(m) определяют величины соответствующих им₁²и₂². Таким образом, мы получили два неравенства, обуславливающих одинаковую надежность определения границ доверительного интервала для_x²с двух сторон (слева и справа):

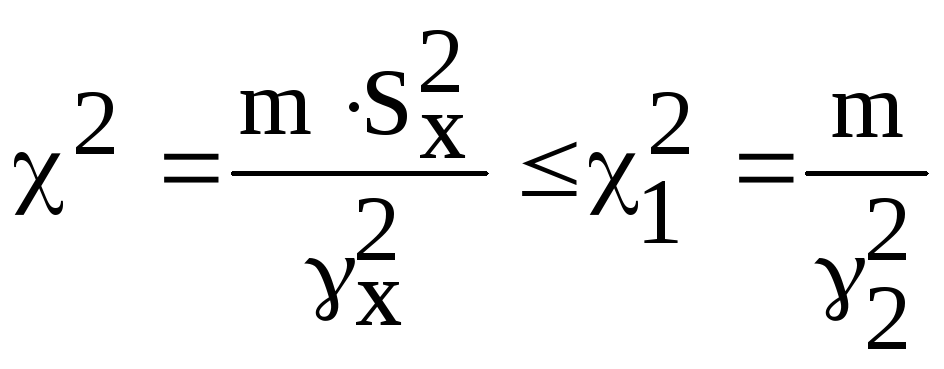(3.24)

с надежностью ₁=(1-P)/2,

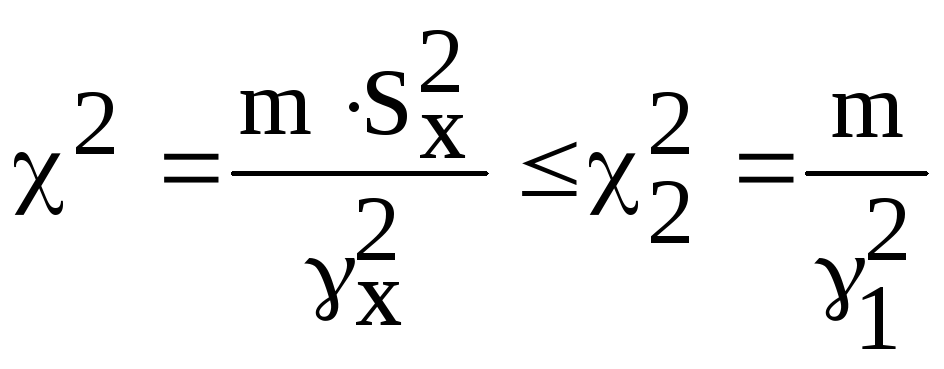(3.25)

с надежностью ₂=1-₁₌1-(1-P)/2=(1+P)/2.

Из неравенств (3.24) и (3.25) получим, что вероятность попадания ²в интервал (₁²;₂²), т.е.

равна разности вышеупомянутых площадей ₂-₁=P. Значения₁²и₂²при различных значениях m и надежности P рассчитаны заранее и приведены в справочниках. Аналогичным образом можно оценить и дисперсию окончательного результата. Так както

Пример 3.4.В серии из десяти измерений (n=10) было получено=5,410^-3мм². Требуется определить, в каком интервале находится фактическое значение дисперсии.

При Р=0,9, m=n-1=9, поэтому на основе (3.24) и (3.25) имеем

Значения ₁²с надежностью₁=(1-Р)/2=0,05 и₂²с надежностью₂=(1+Р)/2=0,95 табулированы и получены нами с помощью статистической функции ХИ2ОБР из электронных таблицMicrosoft Excel(см. п. 7.1). Следовательно, 0,5325,410^-32,7075,410^-3или 2,8710^-31,4610^-2. Аналогично для Р=0,95 получаем 2,5510^-31,8010^-2.

3.5. Сравнение двух рядов наблюдений

При проведении и анализе результатов экспериментальных исследований часто в инженерной практике приходится сравнивать две партии изделий, показания двух или нескольких приборов, анализировать результаты работы однотипных металлургических агрегатов и печей, сравнивать результаты исследований проб материалов и др. Вот некоторые из них.

1. Требуется определить правильно ли показывают приборы, если одновременно осуществляется измерение эталонным прибором, а затем измерение этой же величины осуществили другими приборами и получили ряды наблюдений. Равно ли их математическое ожидание действительному значению измеряемого параметра?

2. Необходимо сравнить показания двух приборов, измеряющих одну и ту же величину. Получено два ряда наблюдений. Одинакова ли точность измерения одного и того же параметра разными приборами?

3. Два агрегата выпускают одну и ту же продукцию. Необходимо сделать вывод о том, какой из них лучше в каком-либо смысле.

Решение задач осуществляется с использованием статистических гипотез.