МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ

Кафедра ПР-7 «Персональная электроника»

УТВЕРЖДАЮ

Заведующий кафедрой ПР-7

_______ (Сахаров Ю. С.)

«___»_________2012г.

Для студентов 3_ курса факультета ПР

Специальности 210201

кандидат технических наук, доцент, Воробьев В.Л.

ЛЕКЦИИ

по дисциплине 2704 «Основы автоматики и САУ»

Обсуждены на заседании кафедры

«__»___________2012г.

Протокол № __

МГУПИ – 2012г.

Основные понятия теории управления

Термин «управление» имеет широкое смысловое содержание и применим для любых организованных систем целенаправленных действий. Поэтому, теория управления (или кибернетика) является достаточно универсальной теорией для систем различного физического содержания и назначения (технических, биологических, социальных и пр.)

В общем случае данная теория содержит общие принципы системной организации. При определении организованной (не хаотической) системы различают структурную и функциональную составляющие.

Структурная составляющая включает совокупность определённых элементов и их взаимосвязи в рамках системы.

Функциональная составляющая включает промежуточные и конечные цели и способы их достижения в пределах выделенной системы.

Функциональная составляющая является базовой и определяет любую организованную систему как «систему целенаправленных действий». Такое определение соответствует так называемому «процессуальному подходу» в современной науке. Первичный характер функциональной составляющей означает, что одни и те же функции можно реализовать различными структурными способами.

В соответствии с процессуальным подходом, обобщённую модель любой системы целенаправленных действий можно представить в процессуальных категориях синтез/анализ.

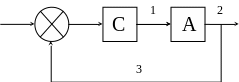
1. Информационные связи (любое управление требует соответствующего информационного обеспечения относительно объектов управления и их взаимодействий с внешней средой).

2. Прямые управляющие связи (предназначены для реализации необходимых целевых функций управления).

3. Обратные корректирующие связи (коррекция траектории объектов управления относительно заданных целевых функций в зависимости от условий взаимодействия объекта с внешней средой).

По существу, данная модель является обобщённой моделью управления, понимая под управлением целенаправленное воздействие на ОУ (объект управления) для достижения заданного или оптимального состояния или траектории ОУ — то есть закона управления. Под ОУ понимают объекты и процессы любой физической природы и сложности. Конкретизируем данную модель и представимо обобщенную структурную схему САУ (системы автоматического управления без участия человека) или АСУ (автоматизированные системы управления с участием человека-оператора).

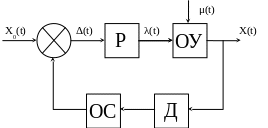
ОУ — объект управления.

Р — регулятор, включающий УУ (устройство управления) для САУ или человека-оператора для АСУ и ИО (исполнительные органы ОУ).

Д — датчики реального состояния ОУ.

ОС — цепь обратной связи.

X₀(t) — заданный закон управления.

X(t) — реальная траектория ОУ.

Δ(t) — сигнал рассогласования между заданным законом управления и реальной траекторией ОУ. Δ(t) = F{X(t) – X₀(t)} → min

λ(t) — сигнал управления на ОУ.

μ(t) — внешнефакторные воздействия или помехи на ОУ.

— сумматор.

Различают, в зависимости от условий управления, замкнутые (с ОС) и разомкнутые (без ОС) системы управления.

Различают следующие виды управления:

1. Жёсткое (программное) управление, реализуемое на основе разомкнутых САУ. Необходимым условием такого управления является: μ(t) → 0. Типичным примером такого управления являются станки с ЧПУ (числовым программным управлением).

2. Регулирование. Данный вид управления является наиболее распространенным, и его реализация подразумевает использование замкнутых систем с заданным законом управления.

3. Настройка. Данный вид управления подразумевает использование замкнутых систем управления, в которых закон управления не задан, но заданы параметры, относительно которых требуется выполнить условие оптимальности (экстремальные условия). Такие системы часто называют системами оптимального управления. Обязательным условием реализации таких систем является наличие в регуляторе, точнее в УУ регулятора, устройств поиска экстремума (УПЭ).

С точки зрения внутреннего содержания процессов управления целесообразно ввести так называемую идентификационную модель. Под идентификацией понимают сравнение априорной (apr) — доопытной или модельной информации и апостериорной (aps) — опытной или экспериментальной информации по критериям близости или различимости.

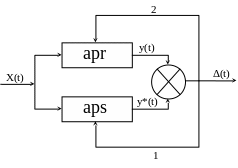
1. Классическая идентификационная модель (подгонка реального состояния ОУ под заданную априорную модель или закон управления).

2. Диагностическая идентификационная модель (оценка реального состояния ОУ относительно априорной модели).

Рассмотрим математические формы критерия близости или рассогласования Δt. В общем случае математической формой данного критерия является функционал разности вида: Δt =F { y(t) – y^*(t) }.

Конкретизацией данной формы являются следующие виды критериев:

а) , где y_i — координатные точки траектории ОУ. Основными недостатками данного критерия является его линейная форма и влияние знака рассогласования априорной и апостериорной информации на величину критерия, поэтому другой формой критерия близости является

б) критерий наименьших квадратов. .

Перечисленные две математические формы критерия являются базовыми в теории управления. Рассмотрим возможности их применение в типичных задачах и системах управления:

1. Высотный канал автопилота летательного аппарата (ЛА).Задача управления подразумевает стабилизацию заданной высоты полета Н.

В данном случае применима классическая идентификационная модель:

apr → H_зад. ± ∆H. Задание допуска ± ∆H является обязательным условием реализации соответствующей системы управления.

aps → H_{реальн.}

∆t = (H_{реальн.} – (H_зад. ± ∆H)) → min

В данном примере влияние знака рассогласования между априорной и апостериорной информацией является принципиальным с точки зрения реализации заданного закона управления (заданного высотного диапазона ЛА). Очевидно, что управление в данном случае осуществляется по классической идентификационной схеме, то есть с корректировкой апостериорной информации в виде реальной высоты ЛА.

2. Управление экспериментом. Данный вид управления так же основан на классической идентификационной модели. Эта задача подразумевает построение математической модели объекта по результатам эксперимента с этим объектом. В качестве исходных данных используются экспериментальные результаты в виде определённого набора случайных величин.

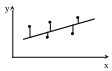
а). Любой эксперимент начинается с формирования в явной математической форме априорной модели. Выбор такой модели является самостоятельной задачей и базируется на физический свойствах объекта. На этом этапе возможны наиболее существенные ошибки. Выберем для примера простейшую форму априорной модели y = ax + b.

б). Строится апостериорная модель объекта, соответствующая априорной форме и максимально приближенная к экспериментальным данным по соответствующему критерию близости Δt. В данном случае целесообразно использовать критерий наименьших квадратов, чтобы устранить влияние знака рассогласования на величину критерия.

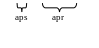
в). Реализуется алгоритм наименьших квадратов.

Конечным результатом реализации данного алгоритма является апостериорная модель, например y = 1,3x – 0,8.

При этом числовые значения коэффициентов апостериорной модели являются оптимальными для данного эксперимента по критерию наименьших квадратов. Очевидно, что данный пример реализован в соответствии с классической идентификационной моделью, то есть с подгонкой апостериорной модели под заданную априорную форму. В случае неизвестной математической формы априорной модели целесообразно использовать аппроксимационные формы, например в виде полинома

y = a_n xⁿ + a_{n - 1} x^{n – 1} + … + a₀; n ≤ 10

Основным недостатком аппроксимационных форм является отсутствие в них явного физического содержания, что в конечном итоге усложняет процедуру управления.

3. Управление качеством в виде разбраковки изделий. Данный пример основан на диагностической идентификационной модели.

а). В качестве исходных данных используется априорная модель диагностируемого объекта. Например в виде линейной ВАХ резистора.

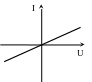
б). Сравниваем идеальную (apr) и реальную (aps) ВАХ диагностируемого резистора

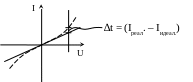
В отличии от первых двух примеров, где критерий ∆t выступал в качестве критерия близости, в данном примере ∆t выступает в качестве критерия различимости, что характерно для диагностической идентификационной модели. По существу, данный критерий является критерием качества диагностируемого изделия и может быть использован для разбраковки.

Таким образом, все процедуры управления можно соотнести с классической или диагностической идентификационной схемой при соответствующей интерпретации критерия ∆t (близости или различимости).

С информационной точки зрения, идентификационная модель характеризует определённый объём информации, получаемый в результате перехода от априорной модели к апостериорной модели. В общем случае, информация определяется неопределённостью соответствующих состояний объекта, поэтому I = ƒ(S_apr) – ƒ(S_aps), где I — количество информации, S_apr и S_aps — неопределённости соответствующих состояний объекта.

С математической точки зрения, для дискретных состояний , где m — количество дискретных состояний объекта, p_k — вероятности соответствующих состояний.

Для непрерывных систем: 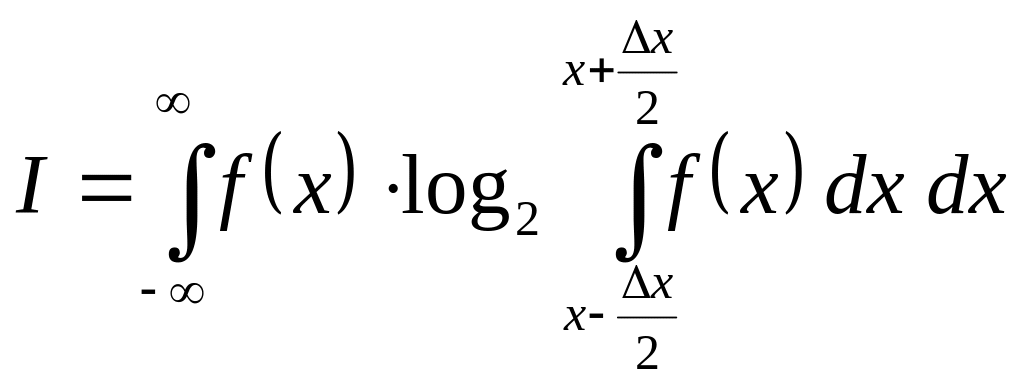, где ƒ(x) — плотность вероятности непрерывных состояний объекта, ∆x — разрешающая способность измерительных приборов или датчиков.

В общем случае и .

Тогда, в простейшем случае, для равномерных распределений в дискретном варианте I = log₂m, в непрерывном .

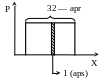
Пример:

m = 2 → apr (2 состояния)

aps → m = 1

I = log₂2 = 1 бит

x = 32 В (apr)

∆x = 1 В (aps)

Таким образом, с информационной точки зрения, идентификационные модели являются моделями получения информации в процессе управления, т.е. любое управление подразумевает как использование, так и получение определённой информации в процессе управления.

Математические модели систем управления

Любой процесс управления в соответствии с процессуальным подходом (см. предыдущий раздел) является временны́м процессом. Поэтому любые модели, как процессов, так и систем управления, должны включать фактор времени в явном виде, то есть модели систем управления являются моделями динамических систем.

Рассмотрим общую математическую форму модели динамических систем, включающую производные различных порядков:

Перейдём к операторной форме динамических моделей, где

-оператор дифференцирования.

Введём базовое для теории управления понятие передаточной функции:

(отношение выходных сигналов к входным)

Тогда в общем случае:

W=y/x=(b_kp^k+b_k-1p^k-1+…+b₀)/(a_npⁿ+a_n-1p^n-1+…+a₀)

Для конкретизации передаточных функций, введём математические формы передаточных функций элементарных линейных звеньев. Термин «элементарные» подразумевает, что набор таких звеньев позволяет создавать сложные передаточные функции любой математической формы.

1. Усилительное звено (безинерционное)

(P = 0)

Для анализа динамики звеньев используется единичная функция 1(t).

Соответственно, реакцию звена на единичную функцию называют переходной характеристикой.

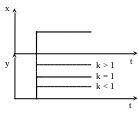
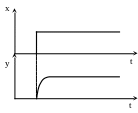
2. Идеальное интегрирующее звено

или

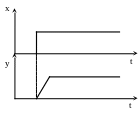
3. Реальное интегрирующее (или апериодическое) звено

(Tp+1)y = kx

W(p) = y/x = k/(Tp+1)

Для получения математической формы переходной характеристики этого звена решим следующее дифференциальное уравнение:

Решение данного уравнения можно представить в виде

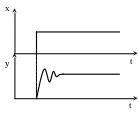
4. Колебательное звено

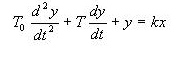
(T₀p²+Tp+1)y = kx

W(p) = y/x = k/(T₀p²+Tp+1) ; Переходная характеристика:

;

;

5. Дифференцирующее звено

Для дифференцирующих звеньев переходные характеристики являются бесконечными, поэтому для описания динамики таких звеньев используется форма в виде реакции объекта на дельта-функцию (δ-функцию).

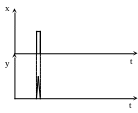
Очевидно, что предыдущие типы звеньев, за исключением усилительного, обладали повышенной инерционностью в смысле затягивания фронта входного сигнала. Дифференцирующее звено, наоборот, обостряет фронт входного импульса, то есть ускоряет динамику переходных процессов.

6. Звено запаздывания

Где τ — время запаздывания

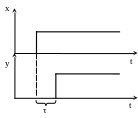
Для получения математической формы передаточной функции данного звена необходимо исходную форму разложить в ряд Тейлора с последующим преобразованием. Тогда получим:

Особенностью данного звена является принципиальная возможность описания с его помощью динамических свойств цифровой техники, в том числе ЭВМ в целом.

Кроме рассмотренных линейных звеньев существуют нелинейные звенья систем управления. Рассмотрим некоторые типовые нелинейные звенья:

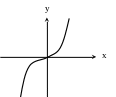
а) звено типа “зоны нечувствительности”

б) звено типа “насыщения”

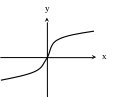
Для математического описания нелинейных звеньев используется способ кусочно-линейной аппроксимации.

,

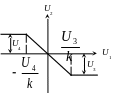
U₂ =

,

,

,

Обратим внимание, что рассматриваемые нелинейные звенья обладают нулевой инерционностью, так как их математические модели формулируются при условии P=0. Инерционные свойства реальных нелинейных систем в соответствии с их эквивалентными схемами формулируются в виде моделей предыдущих линейных типов звеньев.

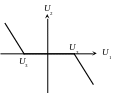
U₂ =

,

,

,

Другим специфическим типом звена систем управления является математическая модель человека-оператора, необходимая для математического описания АСУ. Очевидно, что все свойства человека математически описать невозможно, поэтому используется ограниченная модель человека относительно функций оператора в АСУ. Данная модель отражает поведенческую реакцию оператора на сигналы отклонения определённых параметров от заданных норм или диапазонов. Модель является эмпирической (полученной экспериментально) и включает:

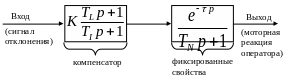
— (звено запаздывания) характеризует реакцию человека на соответствующий сигнал. В среднем τ = 0,14 с.

— (апериодическое звено) характеризует нейромышечную инерцию оператора.

— (дифференцирующее звено) характеризует ускорение динамики оператора за счёт опыта работы и прогнозирования ситуации.

— (апериодическое звено) характеризует ухудшение динамики оператора за счёт утомления.