2.2. Нормальный закон распределения

Функции распределения F(x) и f(x) представляют собой математическую модель, которая описывает экспериментально наблюдаемые величины. Одной из задач статистической обработки данных является нахождение таких функций распределения, которые, с одной стороны, достаточно хорошо описывали наблюдаемые значения случайной величины, а с другой – были бы удобны для дальнейшего статистического анализа. Вид функции распределения предпочтительно выбирать на основе представлений о физической природе рассматриваемого явления, т.к. в этом случае исключаются возможные погрешности при распространении найденных закономерностей за пределы изучаемого интервала варьирования случайных величин.

Среди всех изученных до настоящего времени случайных величин наиболее важное место занимают случайные величины, имеющие так называемое нормальное (Гауссово) распределение(рис.2.5). Нормальному закону подчиняются, как правило, результаты испытаний стали на прочность, производительность многих металлургических агрегатов, составы сырья, топлива, сплавов, массы слитков, отлитых в однотипные изложницы, случайные ошибки измерений и т.п., поэтому исследователи чаще всего используют это распределение при математической обработке результатов наблюдений.

Другие распределения, которые мы будем использовать в дальнейшем (Стьюдента, Фишера, Пирсона, Кохрена, а также критериальные таблицы) составлены на основе именно нормального распределения. Заметим, что в математической статистике сделана оценка для двух противоположных распределений: нормального и равномерного и показано, что оценки результатов исследований в технических задачах отличаются не более, чем на 20% .

Дифференциальная функция (плотность распределения) нормального распределения имеет вид:

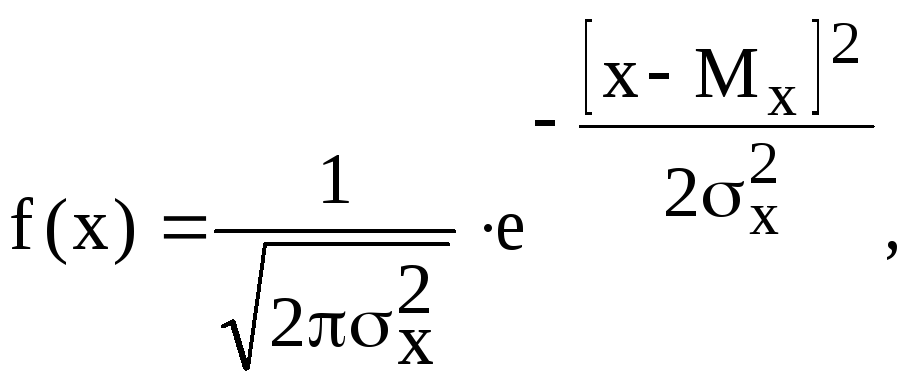(2.14)

Из уравнения (2.14) следует, что плотность распределения вероятностей для нормального распределения случайной величины определяется двумя параметрами М_xи_x².

Интегральная функция нормально распределенной величины имеет вид

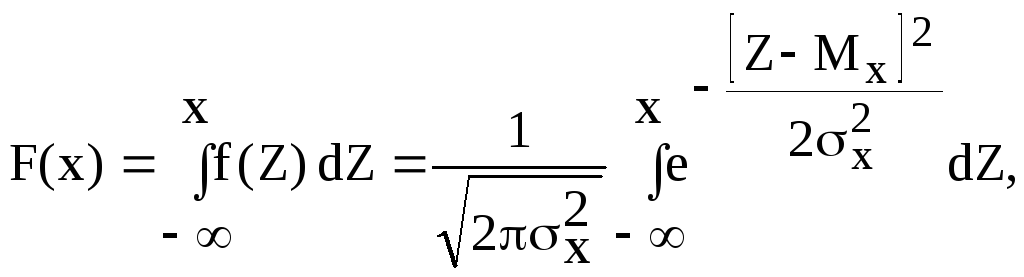(2.15)

Отметим некоторые свойства нормального закона распределения.

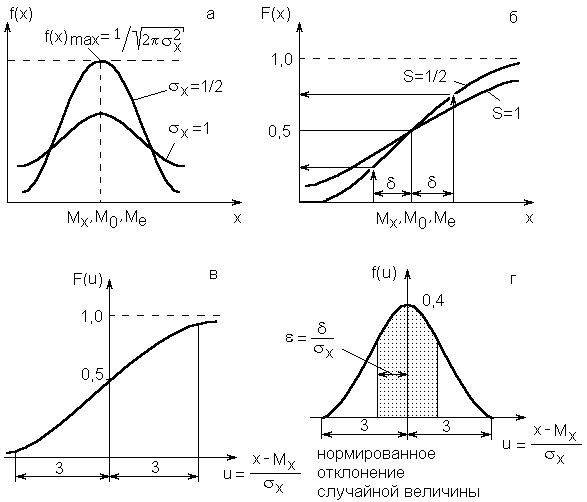
Рис.2.5.Дифференциальная (а,г) и интегральная (б,в) функции при нормальном законе распределения случайных величин

1. Кривая плотности распределения симметрична относительно значения М_x, называемого иногда центром распределения.

2. При больших значениях _x²кривая f(x) более пологая, т.е._x²является мерой величины рассеивания значения случайной величины около значений М_x. При уменьшении параметра_x²кривая нормального распределения сжимается вдоль оси ОХ и вытягивается вдоль f(x).

3. Максимум ординаты кривой плотности распределения определяется выражением

(2.16)

что при _x²=1 соответствует примерно 0,4.

4. Для нормального распределения среднее, мода и медиана совпадают

(2.17)

В ряде случаев рассматривается не сама случайная величина, а ее отклонение от математического ожидания

Такая случайная величина называется центрированной. Очевидно, чтоM_x=0.

Введем нормированноеотклонение (значение) случайной величины, выраженное в долях среднеквадратичного отклонения

(2.18)

Для нормированного отклонения, распределенного по нормальному закону, получаем

(2.19)

(2.20)

Графики этих функций показаны на рис. 2.5в, г.

Значение плотности вероятности и интегральной функции этого распределения, называемого нормированным нормальным распределением, табулированы и приведены в различных учебниках и справочниках по математической статистике.

В ряде случаев важно знать вероятность того, что случайная величина Х не будет отличаться от своего среднего значения М_xбольше, чем на величину, т.е. нормально распределенная случайная величина примет значение на интервале [а;в] (рис.2.6). Эта вероятность называетсядоверительной вероятностью (P) и она показывает вероятность того, что результат измерений отличается от истинного значения на величину, не большую :

(2.21)

Интервал от (M_x-) до (M_x+) называется доверительным интервалом.В дальнейшем уточним эти понятия. Заметим, что доверительная вероятность равна площади, заштрихованной на рис.2.6. Действительно, площадь, ограниченная интервалом, равна вероятности того, что случайная величина находится в этих пределах. Обозначим значение доверительного интервала, выраженного в долях среднеквадратичного отклонения, как

(2.21а)

Тогда, в случае использования нормированного значения случайной величины, выражение (2.21) примет вид

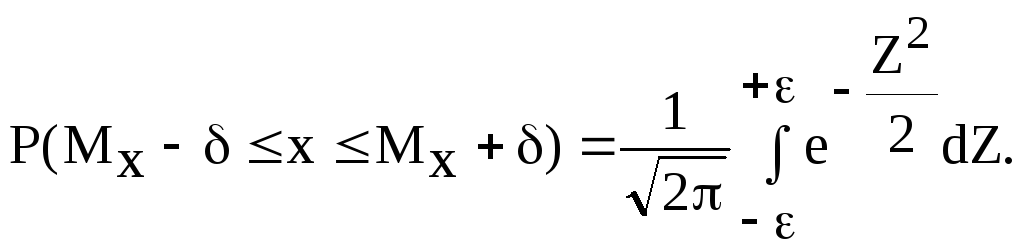(2.22)

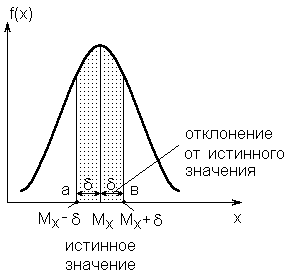
Рис.2.6.К понятию доверительного интервала

Эта функция называется нормированной функцией Лапласаи для облегчения расчетов эта функция представлена таблицами и приведена в справочной литературе. Так, доверительному интервалу, равному значению среднеквадратичного отклонения (=_x=1_x), соответствует доверительная вероятность 0,68. Иными словами, при нормальном законе распределения примерно 2/3 всех значений случайной величины (наблюдений) лежит в площади, отсекаемым перпендикуляром к оси ОХ (M_x=_x). Доверительному интервалу равному=1,96_x2_x, соответствует доверительная вероятность 0,95. Доверительному интервалу 3_xсоответствует доверительная вероятность 0,997 (см. рис. 2.5в,г).

Следовательно, отклонение истинного значения случайной величины от математического ожидания не превосходит утроенного среднего квадратичного отклонения с вероятностью 0,997. Это свойство в математической статистике носит названия правила трех сигм.

Отметим дополнительно, что 90% значений случайной величины лежат в диапазоне между -1,64_xи +1,64_x. Таким образом, чем больше величина доверительного интервала, тем с большей вероятностью величинаxпопадает в этот интервал.

Рассмотрим небольшой пример

Пример 2.2.Предположим, что математическое ожидание содержания кремния в чугуне равноM_Si=0,6%, а среднеквадратичное отклонение_Si=0,15%. В этом случае, мы можем быть уверены в том, что величина измеренного содержания кремния в чугуне будет находиться в интервалах:

0,6 0,680,15 = 0,60,10 с вероятностью 68%;

0,6 1,640,15 = 0,60,29 с вероятностью 90%;

0,6 1,960,15 = 0,60,29 с вероятностью 95%;

0,6 3,000,15 = 0,60,45 с вероятностью 99,7%,

т.е. из 1000 проб только 3 пробы по содержанию кремния в чугуне будут выходить из диапазона от 0,15 до 1,05%.

Заметим однако, что мы предполагали нормальность закона распределения измерений, а также то, что изначально были известны математическое ожиданиеM_xи среднеквадратичное отклонение_x, т.е. выполнено большое (в пределе бесконечное) число измерений. Как же быть в реальных условиях, когда число измерений весьм3. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА

ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Предварительная обработка результатов измерений и наблюдений необходима для того, чтобы в дальнейшем с наибольшей эффективностью, а главное корректно, использовать для построения эмпирических зависимостей статистические методы и корректно проанализировать полученные результаты.

Содержание предварительной обработки состоит в отсеивании грубых погрешностей, оценке достоверности результатов измерений. Другим важным моментом предварительной обработки данных является проверка соответствия распределения результатов измерения закону нормального распределения и определения параметров распределения. Если эта гипотеза неприемлема, то следует определить какому закону распределения подчиняются опытные данные и, если это возможно, преобразовать данное распределение к нормальному.