4.4. Линейная регрессия от одного фактора

Уравнение линии регрессии на плоскости в декартовых координатах имеет вид выражения (4.5).

Задачу метода наименьших квадратов аналитически можно выразить следующим образом:

(4.13)

Для решения этой задачи, как известно из математического анализа, необходимо вычислить частные производные функции Ф по коэффициентам b₀, b₁и приравнять их нулю:

(4.14)

Система нормальных уравнений (4.8) в этом случае примет вид

(4.15)

Решение этой системы относительно b₀и b₁ дает

(4.16а)

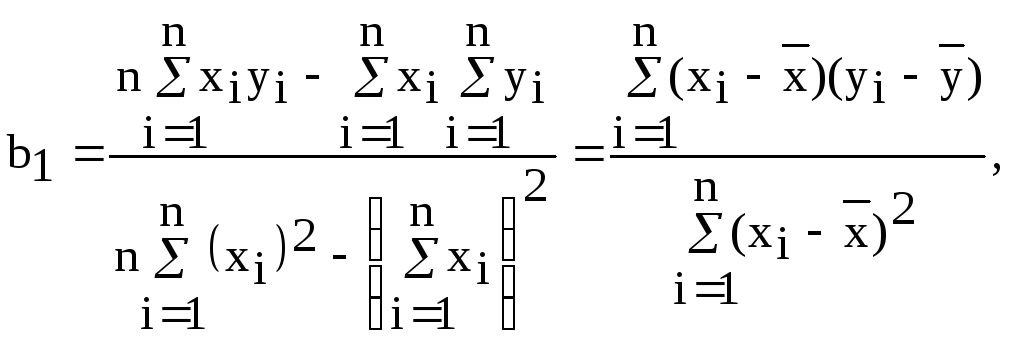(4.16б)

т.е. необходимо определить

Коэффициент b₀(свободный член уравнения регрессии) геометрически представляет собой расстояние от начала координат до точки пересечения линии регрессии с ординатой, а коэффициент b₁характеризует тангенс угла наклона линии регрессии к оси OX.

Если же определяют уравнение регрессии в виде

то система уравнений для нахождения b₀, b₁, b₁₁будет иметь вид

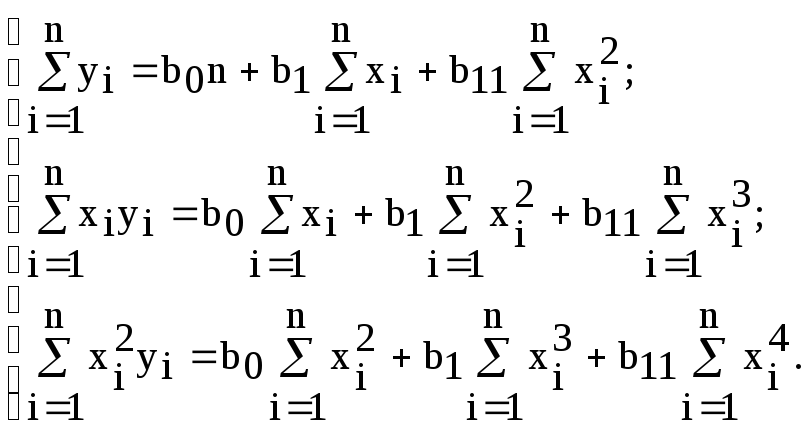(4.16в)

Из уравнений (4.15) и (4.16в) вытекает правило записи любых систем: необходимо записать столько уравнений в системе, сколько неизвестных членов в искомом уравнении, всякий раз суммируя произведения членов исходного уравнения на переменную при искомом коэффициенте.

Оценку силы линейной связиосуществляют повыборочному (эмпирическому) коэффициенту парной корреляцииr_xy. Выборочный коэффициент корреляции может быть вычислен двумя способами.

1. Как частный случай корреляционного отношения для линейного уравнения регрессии.

С учетом того, что ,

(4.17)

величина отношения будет равна

(4.18)

где S_xи S_y– выборочные средние квадратичные отклонения.

2. Как среднее значение произведения центрированных случайных величин, отнесенное к произведению их среднеквадратичных отклонений:

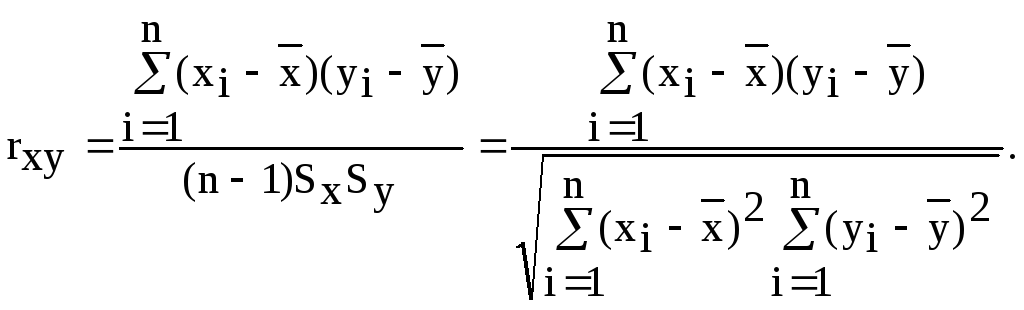(4.19)

Покажем, что обе последние формулы эквивалентны. Для этого преобразуем выражение (4.19) к виду

Подставляя последнее выражение в формулу (4.16б), имеем

Как правило, по результатам экспериментов находят S_x, S_y,и рассчитывают r_xyпо формуле (4.19), а затем, используя эти величины, определяют коэффициенты уравнения регрессии

(4.20)

Коэффициент корреляции r_xyизменяется в пределах -1r_xy+1.

Положительная корреляция между случайными величинами характеризует такую стохастическую зависимость между величинами, когда с возрастанием одной из них другая в среднем также будет возрастать. При отрицательной корреляции с возрастанием одной случайной величины другая в среднем будет уменьшаться. Чем ближе значение r_xyк единице, тем теснее статистическая связь.

Отметим еще раз область применимости выборочного коэффициента корреляции для оценки тесноты связи.

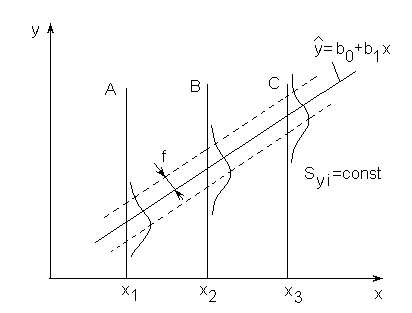
1. Коэффициент парной корреляции значений y и x применительно к однофакторной зависимости характеризует тесноту группирования данных лишь относительно прямой (например линия A на рис.4.8a). При более сложной зависимости (рис.4.8б) коэффициент корреляции r_xyбудет оценивать тесноту экспериментальных точек относительно некоторой прямой, обозначенной буквой А, что, естественно, несет мало сведений о тесноте их группирования относительно искомой кривой

Рис.4.8.К понятию коэффициента парной корреляции

Рис.4.9. К понятию коэффициента парной корреляции в случае двумерного нормального распределения параметров

2. Коэффициент парной выборочной корреляции имеет четкий физический смысл только в случае двумерного нормального распределения параметров, т.е. когда для каждого значения Х существует совокупность нормального распределения Y и наоборот, а дисперсия зависимой переменной при изменении значения аргумента остается постоянной (рис.4.9).

Даже при выполнении этих, вообще говоря достаточно жестких условий, не всякое значение выборочного коэффициента корреляции является достаточным для статистического обоснования выводов о наличии действительно надежной корреляционной связи между фактором и откликом. Надежность статистических характеристик ослабевает с уменьшением объема выборки (n). Так, при n=2 через две экспериментальные точки можно провести только одну прямую и зависимость будет функциональной, при этом выборочный коэффициент корреляции равен единице r_xy=1. Однако это не означает надежность полученных статистических характеристик в силу весьма и весьма ограниченного объема выборки. Значит, вычислять коэффициент корреляции по результатам двух наблюдений бессмысленно, так как он заведомо будет равен единице, и это будет обусловлено не свойствами переменных и их взаимным отношением, а только числом наблюдений.

В связи с этим требуется проверка того, насколько значимо отличается выборочный коэффициент корреляции r_xyот его действительного значения r_xy^*. При достаточно большом объеме выборки nN, где N – достаточно большое число, r_xy^*=r_xy. Таким образом, требуется проверка значимости выборочного коэффициента парной корреляции и оценка его доверительного интервала.

Для определения значимостиr_xy сформулируем нуль-гипотезу Н₀: r_xy=0, т.е. корреляция отсутствует. Для этого рассчитывается экспериментальное значение t-критерия Стьюдента

(4.21)

и сравнивается с теоретическим при числе степеней свободы n-2.

Если t_экспt_;n-2, то нулевая гипотеза отклоняется, а гипотеза, что коэффициент корреляции существенен, принимается.

Для определения доверительного интервала коэффициента корреляцииР.Фишер предложил такое нелинейное преобразование величины r_xy, при котором закон распределения этой оценки, вообще говоря, довольно сложный, практически приближается к нормальному. Это преобразование производится по формуле

(4.22)

(см. также статистическую функцию ФИШЕР из электронных таблиц Microsoft Excelв п. 7.1).

Среднеквадратичное отклонение случайной величины Z* зависит от числа опытов

(4.23)

а математическое ожидание очень близко к числу, получающемуся после подстановки в формулу (4.22) вместо r_xyистинного значения коэффициента корреляции r_xy^*. Эти свойства величины Z* позволяют просто оценить, в каких пределах может находиться истинное значение коэффициента корреляции, если по n опытам получены некоторые значения его выборочного значения (оценки) r_xy. Если граничное значение r_xyимеет тот же знак, что и r_xy*, то можно считать в первом приближении, что корреляционная связь между переменными достоверна.

Пример.4.1.При обработке 17 пар данных x и y получены следующие значения n=17;Выборочный коэффициент корреляции r_xy=-0,94, т.е. величина y связана с x достаточно сильной причинной связью, близкой к функциональной зависимости.

Определение значимости коэффициента r_xy.

;

t_0,05;15=1,75.

Так как t_эксп>t_;n-2, то коэффициент корреляции существенен.

Определение доверительного интервала. По формулам (4.22) и (4.23) определим величину Z*

и ее среднеквадратичное отклонение

Зададимся вероятностью того, что истинное значение Z отличается от вычисленного на основании оценки коэффициента корреляции Z* не более, чем на _Z. Учитывая нормальный закон распределения Z, имеем при вероятности

95%: _Z=1,96S_Z=1,960,267=0,523;

90%: _Z=1,670,267=0,446;

99,7%: _Z=3,000,267=0,801.

Таким образом, истинное значение Z с вероятностью, например 95%, лежит в пределах Z₁ZZ₂, где Z₁=1,738-0,523=1,215 и Z₂=1,738+0,523=2,261.

Этим двум значениям Z соответствуют коэффициенты корреляции, полученные из формулы (4.22) -0,84r_xy-0,98. Следовательно, доверительные интервалы подтверждают достаточно сильную причинную связь между анализируемыми параметрами.

Таким образом, корреляционный анализ устанавливает связь между исследуемыми случайными переменными и оценивает тесноту этой связи.