7.1. Статистические функции Microsoft Excel

ВЕРОЯТНОСТЬ(x_интервал; интервал_вероятностей; нижний_предел; верхний_предел).

Результат: Возвращает вероятность того, что значение из интервала находится внутри заданных пределов. Если верхний_предел не задан, то возвращается вероятность того, что значения в аргументе x_интервал равняются значению аргумента нижний_предел.

Аргументы: x_интервал – это интервал числовых значений x, с которыми связаны вероятности. Интервал_вероятностей – это множество вероятностей, соответствующих значениям в аргументе x_интервал. Нижний_предел – это нижняя граница значения, для которого вычисляется вероятность. Верхний_предел – это необязательная верхняя граница значения, для которого требуется вычислить вероятность.

ДИСП(число1; число2; ...)

Результат: Оценивает дисперсию по выборке.

Аргументы: Число1, число2, ... – это от 1 до 30 числовых аргументов, соответствующих выборке из генеральной совокупности. ДИСП предполагает,что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, необходимо вычислять дисперсию, используя функцию ДИСПР. Для вычисления функции ДИСП используется выражение (3.2б).

ДИСПР(число1; число2; ...)

Результат: Вычисляет дисперсию для генеральной совокупности.

Аргументы: Число1, число2, ... – это от 1 до 30 числовых аргументов, соответствующих генеральной совокупности.

Функция ДИСПР предполагает, что аргументы представляют всю генеральную совокупность. Если данные представляют только выборку из генеральной совокупности, то дисперсию следует вычислять используя функцию ДИСП.

Уравнение для расчета функции ДИСПР представлено выражением (3.2а).

ДОВЕРИТ(альфа; станд_откл;размер)

Результат: Возвращает доверительный интервал для среднего генеральной совокупности.

Аргументы: Альфа – это уровень значимости используемый для вычисления уровня надежности. Напомним, что уровень надежности равняется 100(1-альфа) процентам, или, другими словами, альфа равное 0,05 означает 95-процентный уровень надежности. Станд_откл – это стандартное отклонение генеральной совокупности для интервала данных (см. выражение (3.3б)), предполагается известным. Размер – это размер выборки.

КВАДРОТКЛ(число1; число2;...)

Результат: Возвращает сумму квадратов отклонений точек данных от их среднего.

Аргументы: Число1, число2, ... – это от 1 до 30 аргументов, для которых вычисляется сумма квадратов отклонений. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой. Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.

Уравнение для суммы квадратов отклонений имеет следующий вид:

КВАДРОТКЛ=где n – количество аргументов.

КВПИРСОН(известные_значения_y; известные_значения_x)

Результат: Возвращает квадрат коэффициента корреляции Пирсона для точек данных в аргументах известные_значения_y и известные_значения_x. Для получения более подробной информации см. ПИРСОН. Значение r-квадрат можно интерпретировать как отношение дисперсии для y к дисперсии для x.

Аргументы: Известные_значения_y – это массив или интервал точек данных. Известные_значения_x – это массив или интервал точек данных. Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.

КОРРЕЛ(массив1; массив2)

Результат: Возвращает коэффициент корреляции между интервалами ячеек массив1 и массив2. Напомним, что коэффициент корреляции используется для определения наличия линейной взаимосвязи между двумя свойствами (см. главу 4) и рассчитывается по выражению (4.19).

Аргументы: Массив1 – это ячейка интервала значений. Массив2 – это второй интервал ячеек со значениями. Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.

ЛГРФПРИБЛ(известные_значения_y; известные_значения_x; конст; статистика)

Результат: В регрессивном анализе вычисляет экспоненциальную кривую, аппроксимирующую данные и возвращает массив значений, описывающий эту кривую. Поскольку данная функция возвращает массив значений, она должна вводиться как формула для работы с массивами. Уравнение кривой следующее:

y = b*m^xили y = (b*(m₁^x1)*(m₂^x2)* … *(m_n^xn)*) (при наличии нескольких значений x),

где зависимые значения y являются функцией независимых значений x. Значения m являются основанием для возведения в степень x, а значения b постоянны. Отметим, что y, x и m могут быть векторами. Функция ЛГРФПРИБЛ возвращает массив {m_n;m_n-1; ... ;m₁; b}.

Аргументы: Известные_значения_y – это множество значений y, которые уже известны для соотношения y = b*m^x. Если массив известные_значения_y имеет один столбец, то каждый столбец в массиве известные_значения_x интерпретируется как отдельная переменная. Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.

Известные_значения_x – это необязательное множество значений x, которые уже известны для соотношения y = b*m^x. Массив известные_значения_x может включать одно или более множеств переменных. Если используется только одна переменная, то известные_значения_y и известные_значения_x могут быть интервалами любой формы, если только они имеют одинаковые размерности. Если используется более одной переменной, то аргумент известные_значения_y должен быть интервалом ячеек высотой в одну строку или шириной в один столбец (так называемым вектором). Если аргумент известные_значения_x опущен, то предполагается, что это массив {1;2;3;...} такого же размера, как и известные_значения_y.

Конст – это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 1. Если конст имеет значение ИСТИНА или опущено, то b вычисляется обычным образом. Если конст имеет значение ЛОЖЬ, то b полагается равным 1 и значения m подбираются так, чтобы удовлетворить соотношению y = m^x.

Статистика – это логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии. Если статистика имеет значение ИСТИНА, то функция ЛГРФПРИБЛ возвращает дополнительную статистику по регрессии, то есть возвращает массив вида (см. статистическую функцию ЛИНЕЙН)

{m_n;m_n-1;...;m₁;b:se_n;se_n-1;...;se₁; se_b:r2;se_y:F;df:ss_reg;ss_resid}.

Если статистика имеет значение ЛОЖЬ или опущено, то функция ЛГРФПРИБЛ возвращает только коэффициенты m и константу b.

Чем больше график экспериментальных данных напоминает экспоненциальную кривую, тем лучше вычисленная кривая будет аппроксимировать данные. Так же, как функция ЛИНЕЙН, функция ЛГРФПРИБЛ возвращает массив, который описывает зависимость между значениями, но ЛИНЕЙН подгоняет прямую линию к имеющимся данным, а ЛГРФПРИБЛ подгоняет экспоненциальную кривую.

Методы, которые используются для проверки уравнений, полученных с помощью функции ЛГРФПРИБЛ, такие же, как и для функции ЛИНЕЙН. Однако, дополнительная статистика, которую возвращает функция ЛГРФПРИБЛ, основана на следующей линейной модели:

ln y = x₁ln(m₁) + ... + x_nln(m_n)+ ln(b).

Это следует помнить при оценке дополнительной статистики, особенно значений se_iи se_b, которые следует сравнивать с ln(m_i) и ln(b), а не с m_iи b.

ЛИНЕЙН(известные_значения_y; известные_значения_x; конст; статистика)

Результат: Рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, который описывает полученную прямую. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива. Уравнение для прямой линии имеет следующий вид:

y = mx + b или y = m₁x₁+ m₂x₂+ ... + b (в случае нескольких интервалов значений x),

где зависимое значение y является функцией независимого значения x. Значения m – это коэффициенты, соответствующие каждой независимой переменной x, а b – это постоянная. Заметим, что y, x и m могут быть векторами. Функция ЛИНЕЙН возвращает массив {m_n;m_n-1;...;m₁;b}. ЛИНЕЙН может также возвращать дополнительную регрессионную статистику.

Аргументы: Известные_значения_y – это множество значений y, которые уже известны для соотношения y = mx + b. Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная. Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.

Известные_значения_x – это необязательное множество значений x, которые уже известны для соотношения y = mx + b. Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то известные_значения_y и известные_значения_x могут быть массивами любой формы при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (то есть интервалом высотой в одну строку или шириной в один столбец). Если известные_значения_x опущены, то предполагается, что это массив {1;2;3;...} такого же размера как и известные_значения_y.

Конст – это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если конст имеет значение ИСТИНА или опущено, то b вычисляется обычным образом. Если конст имеет значение ЛОЖЬ, то b полагается равным 0 и значения m подбираются так, чтобы выполнялось соотношение y = mx.

Статистика – это логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии. Если статистика имеет значение ИСТИНА, то функция ЛИНЕЙН возвращает дополнительную регрессионную статистику, так что возвращаемый массив будет иметь вид:

{m_n;m_n-1;...;m₁;b:se_n;se_n-1;...;se₁; se_b:r2;se_y:F;df:ss_reg;ss_resid}.

Если статистика имеет значение ЛОЖЬ или опущена, то функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.

Дополнительная регрессионная статистика включает в себя следующие характеристики:

• se₁,se₂,...,se_n– стандартные значения ошибок для коэффициентов m₁,m₂,...,m_n;

• se_b– стандартное значение ошибки для постоянной b;

• r2 – коэффициент детерминированности, который измеряет долю разброса относительно среднего значения, которую "объясняет" полученная регрессия. Коэффициент детерминированности равен квадрату выборочного корреляционного отношения (см. выражение (4.12)), поэтому он нормирован от 0 до 1. Данный коэффициент является очень важным статистическим параметром при оценке регрессионной модели: чем ближе r2 к 1, тем лучше регрессионная модель "объясняет" зависимость в данных;

• se_y– стандартная ошибка (стандартное или среднеквадратичное отклонение) для оценки y;

• F – F-статистика, или F-наблюдаемое значение. F-статистика используется для проверки гипотезы о том, является ли наблюдаемая взаимосвязь между зависимой и независимой переменными случайной или нет;

• Df – степени свободы. Степени свободы полезны для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели нужно сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН;

• ss_reg– регрессионная сумма квадратов, вычисляемая по выражению

где n – число экспериментальных точек;

• ss_resid– остаточная сумма квадратов, вычисляемая по выражению

где n – число экспериментальных точек;

В приведенной ниже таблице показано, в каком порядке на листе электронной таблицы возвращается дополнительная регрессионная статистика.

Mn	mn-1	…	m2	m1	b
Sen	sen-1	…	se2	se1	seb
r2	sey
F	df
ssreg	ssresid

Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель, используемая функцией ЛИНЕЙН. Функция ЛИНЕЙН использует метод наименьших квадратов для определения наилучшей аппроксимации данных. Когда имеется только одна независимая переменная x, коэффициенты m и b вычисляются по выражениям соответственно (4.16б) и (4.16а).

Проводя регрессионный анализ, Microsoft Excelвычисляет для каждой точки квадрат разности между прогнозируемым значениеми фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов ss_resid. ЗатемMicrosoft Excelподсчитывает сумму квадратов разностей между фактическими значениями y и средним значением, которая называется общей суммой квадратов (регрессионная сумма квадратов ss_reg+ остаточная сумма квадратов ss_resid). Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента детерминированности r2, который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными.

МАКС(число1;число2; ...)

Результат: Возвращает наибольшее значение из набора значений.

Аргументы: Число1, число2, ... – это от 1 до 30 чисел, среди которых ищется максимальное значение.

МЕДИАНА(число1; число2; ...)

Результат: Возвращает медиану заданных чисел. Медиана – это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана (см. выражения (2.10) и (2.11) в п. 2.1).

Аргументы: Число1, число2, ... – это от 1 до 30 чисел, для которых определяется медиана. Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.

МИН(число1; число2; ...)

Результат: Возвращает наименьшее значение в списке аргументов.

Аргументы: Число1, число2, ... – это от 1 до 30 чисел, среди которых ищется минимальное значение.

МОДА(число1; число2; ...)

Результат: Возвращает наиболее часто встречающееся или повторяющееся значение в массиве или интервале данных. Также как и функция МЕДИАНА, функция МОДА является мерой взаимно расположения значений (см. п. 2.1).

Аргументы: Число1, число2, ... – это от 1 до 30 аргументов, для которых вычисляется мода. Можно использовать один массив или одну ссылку на массив вместо аргументов, разделяемых точкой с запятой. Аргументы должны быть числами, именами, массивами или ссылками, которые содержат числа.

В наборе значений мода – это наиболее часто встречающееся значение; медиана – это значение в середине массива; среднее – это среднее арифметическое значение. Ни одно из этих чисел не характеризует в полной мере то, в какой степени центрированы данные. Например, если данные сгруппированы в трех областях, одна половина данных близка к некоторому малому значению, а другая половина данных близка к двум другим большим значениям. Обе функции СРЗНАЧ и МЕДИАНА могут вернуть значение из относительно пустой середины, а функция МОДА скорее всего вернет доминирующее малое значение.

НАКЛОН(известные_значения_y; известные_значения_x)

Возвращает наклон линии линейной регрессии для точек данных в аргументах известные_значения_y и известные_значения_x. Наклон определяется как частное от деления расстояния по вертикали на расстояние по горизонтали между двумя любыми точками прямой, то есть наклон – это скорость изменения значений вдоль прямой.

Аргументы: Известные_значения_y – это массив или интервал ячеек, содержащих числовые зависимые точки данных. Известные_значения_x – это множество независимых точек данных. Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа. Величина наклона линии регрессии определяется по выражению (4.16б).

НОРМАЛИЗАЦИЯ(x; среднее; стандартное_откл)

Результат: Возвращает нормализованное значение для распределения, характеризуемого средним и стандартным отклонением.

Аргументы: X – это нормализуемое значение. Среднее – это среднее арифметическое распределения. Стандартное_откл – это стандартное отклонение распределения. Уравнение для нормализованного значения имеет следующий вид:

НОРМОБР(вероятность; среднее; стандартное_откл)

Результат: Возвращает обратное нормальное распределение для указанного среднего и стандартного отклонения.

Аргументы: Вероятность – это вероятность, соответствующая нормальному распределению. Среднее – это среднее арифметическое распределения. Стандартное_откл – это стандартное отклонение распределения.

НОРМОБР использует метод итераций для вычисления функции. Если задано значение вероятности, то функция НОРМОБР производит итерации, пока не получит результат с точностью ± 3*10^-7. Если НОРМОБР не сходится после 100 итераций, то функция возвращает значение ошибки #Н/Д.

НОРМРАСП(x; среднее; стандартное_откл; интегральная)

Результат: Возвращает значение нормальной функции распределения для указанного среднего и стандартного отклонения. Эта функция имеет очень широкий круг приложений в статистике, включая проверку гипотез (см. п. 3.7).

Аргументы: x – это значение, для которого строится распределение. Среднее – это среднее арифметическое распределения. Стандартное_откл – это стандартное отклонение распределения. Интегральная – это логическое значение, определяющее форму функции. Если интегральная имеет значение ИСТИНА, то функция НОРМРАСП возвращает интегральную функцию распределения (см. выражение (2.15)); если это аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения (см. выражение (2.14)).

НОРМСТОБР(вероятность)

Результат: Возвращает обратное значение стандартного нормального распределения u (см. выражение (2.19)). Это распределение имеет среднее равное нулю и стандартное отклонение равное единице.

Аргументы: Вероятность – это вероятность, соответствующая нормальному распределению.

НОРМСТОБР использует метод итераций для вычисления функции. Если задано значение вероятности, то функция НОРМСТОБР производит итерации, пока не получит результат с точностью ± 3*10^-7. Если НОРМСТОБР не сходится после 100 итераций, то функция возвращает значение ошибки #Н/Д.

НОРМСТРАСП(u)

Результат: Возвращает стандартное нормальное интегральное распределение. Это распределение имеет среднее равное нулю и стандартное отклонение равное единице. Эта функция используется вместо таблицы для стандартной нормальной кривой.

Аргументы: u – это значение, для которого строится распределение (см. п 2.2). Значение плотности стандартного нормального распределения определяется выражением (2.20).

ОТРЕЗОК(известные_значения_x;известные_значения_y)

Результат: Вычисляет точку пересечения линии с осью y, используя известные_значения_x и известные_значения_y. Точка пересечения находится на оптимальной линии регрессии, проведенной через известные_значения_x и известные_значения_y. Функция используется, когда нужно определить значение зависимой переменной при значении независимой переменной равном 0 (нулю).

Аргументы: Известные_значения_y – это зависимое множество наблюдений или данных. Известные_значения_x – это независимое множество наблюдений или данных. Уравнение для точки пересечения линии линейной регрессии имеет следующий вид:

B₀

где коэффициент b₁вычисляется по выражению (4.16б).

ПИРСОН(массив1; массив2)

Результат: Возвращает коэффициент корреляции Пирсона r (выборочный коэффициент корреляции), безразмерный индекс в интервале от -1,0 до 1,0 включительно, который отражает степеньлинейной зависимостимежду двумя множествами данных (см. п. 4.4) и определяется выражением (4.19).

Аргументы: Массив1 – это множество независимых значений. Массив2 – это множество зависимых значений. Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.

РАНГ(число; ссылка; порядок)

Результат: Возвращает ранг числа в списке чисел. Ранг числа – это его величина относительно других значений в списке. (Если список отсортировать, то ранг числа будет его позицией.)

Аргументы: Число – это число, для которого определяется ранг. Ссылка – это массив или ссылка на список чисел. Нечисловые значения в ссылке игнорируются. Порядок – это число, определяющее способ упорядочения.

РАНГ присваивает повторяющимся числам одинаковый ранг. Однако, наличие повторяющихся чисел влияет на ранг последующих чисел. Например, для списка целых, если число 10 появляется дважды и имеет ранг 5, то 11 будет иметь ранг 7 (и никакое число не будет иметь ранг 6).

СРГЕОМ(число1; число2; ...)

Результат: Возвращает среднее геометрическое значений массива или интервала положительных чисел.

Аргументы: Число1, число2, ... – это от 1 до 30 аргументов, для которых вычисляется среднее геометрическое. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой. Уравнение для среднего геометрического имеет следующий вид:

СРГЕОМ=

СРЗНАЧ(число1; число2; ...)

Результат:Возвращает среднее арифметическое своих аргументов, вычисляемое по выражению (3.1).

Аргументы: Число1, число2, ... – это от 1 до 30 аргументов, для которых вычисляется среднее. Аргументы должны быть числами или именами массивов, массивами или ссылками, содержащими числа. Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако, ячейки, которые содержат нулевые значения учитываются.

СРОТКЛ(число1; число2; ...)

Результат: Среднее абсолютных значений отклонений точек данных от среднего. Функция СРОТКЛ является мерой разброса множества данных и вычисляется по выражению:

где n – количество аргументов функции.

Аргументы: Число1, число2, ... – это от 1 до 30 аргументов, для которых определяется среднее абсолютных отклонений. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

СТАНДОТКЛОН(число1; число2; ...)

Результат: Оценивает стандартное отклонение по выборке. Стандартное отклонение – это мера того, насколько широко разбросаны точки данных относительно их среднего (см. п. 3.1).

Аргументы: Число1, число2, ... – это от 1 до 30 числовых аргументов, соответствующих выборке из генеральной совокупности. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

Функция СТАНДОТКЛОН предполагает, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНП. Функция СТАНДОТКЛОН использует для расчета формулу (3.3б).

СТАНДОТКЛОНП(число1; число2; ...)

Результат: Вычисляет стандартное отклонение по генеральной совокупности. Аргументы: Число1, число2, ... – это от 1 до 30 числовых аргументов, соответствующих генеральной совокупности. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

Функция СТАНДОТКЛОНП предполагает, что аргументы образуют всю генеральную совокупность. Если данные являются только выборкой из генеральной совокупности, то стандартное отклонение следует вычислять с использованием функции СТАНДОТКЛОН.

Для больших выборок функции СТАНДОТКЛОН и СТАНДОТКЛОНП возвращают примерно равные значения. Функция СТАНДОТКЛОНП использует для расчета формулу (3.3а).

СТЬЮДРАСП(x; степени_свободы; хвосты)

Результат: Возвращает t-распределение Стьюдента. Распределение Стьюдента используется для проверки гипотез для небольших выборок, как правило n<30 (см. п. 3.3).

Аргументы: x – это численное значение, для которого требуется вычислить распределение. Степени_свободы – это целое, указывающее количество степеней свободы. Хвосты – это число возвращаемых хвостов распределения. Если хвосты = 1, то функция СТЬЮДРАСП возвращает одностороннее распределение. Если хвосты = 2, то функция СТЬЮДРАСП возвращает двустороннее распределение.

СТЬЮДРАСП вычисляется следующим образом: СТЬЮДРАСП=p(x<X ), где X – это случайная величина, соответствующая t-распределению.

СТЬЮДРАСПОБР(вероятность; степени_свободы)

Результат: Возвращает обратное распределение Стьюдента для заданного числа степеней свободы.

Аргументы: Вероятность – это вероятность, соответствующая двустороннему распределению Стьюдента. Степени_свободы – это число степеней свободы, характеризующее распределение.

Функция СТЬЮДРАСПОБР вычисляется следующим образом: СТЬЮДРАСПОБР = p(t<X), где X – это случайная величина, соответствующая t_распределению. СТЬЮДРАСПОБР использует метод итераций для вычисления функции. Если задано значение вероятности, то функция СТЬЮДРАСПОБР производит итерации, пока не получит результат с точностью ± 3*10^-7. Если СТЬЮДРАСПОБР не сходится после 100 итераций, то функция возвращает значение ошибки #Н/Д.

Эту функцию можно использовать вместо таблицы критических (теоретических) значений для t-распределения. В частности, для примера 3.1 вычислим теоретическое значение критерия Стьюдента при уровне значимости =0,05 и степени свободы m=5:

t_0,05;5= СТЬЮДРАСПОБР(0,05;5)=2,57.

ТЕНДЕНЦИЯ(известные_значения_y; известные_значения_x; новые_значения_x; конст)

Результат: Возвращает значения в соответствии с линейным трендом. Аппроксимирует прямой линией (по методу наименьших квадратов) массивы известные_значения_y и известные_значения_x. Возвращает значения y, в соответствии с этой прямой для заданного массива новые_значения_x.

Аргументы: Известные_значения_y – это множество значений y, которые уже известны для соотношения y = mx + b. Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная. Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.

Известные_значения_x – это необязательное множество значений x, которые уже известны для соотношения y = mx + b. Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то известные_значения_y и известные_значения_x могут быть массивами любой формы, при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (то есть интервалом высотой в одну строку или шириной в один столбец).

Новые_значения_x – это новые значения x, для которых ТЕНДЕНЦИЯ возвращает соответствующие значения y. Новые_значения_x должны содержать столбец (или стоку) для каждой независимой переменной, так же как известные_значения_x. Таким образом, если известные_значения_y имеет один столбец, то известные_значения_x и новые_значения_x должны иметь одинаковое количество столбцов. Если известные_значения_y имеет одну строку, то известные_значения_x и новые_значения_x должны иметь одинаковое количество строк.

Конст – это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если конст имеет значение ИСТИНА или опущена, то b вычисляется обычным образом. Если конст имеет значение ЛОЖЬ, то b полагается равным 0, и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.

Можно использовать функцию ТЕНДЕНЦИЯ для аппроксимации полиномиальной кривой, проводя регрессионный анализ для той же переменной, возведенной в различные степени. Например, пусть столбец A содержит значения y, а столбец B содержит значения x. Можно ввести x²в столбец C, x³в столбец D, и так далее, а затем провести регрессионный анализ столбцов от B до D со столбцом A.

Формулы, которые возвращают массивы, должны быть введены как формулы массивов.

ТТЕСТ(массив1; массив2; хвосты; тип)

Результат: Возвращает вероятность, соответствующую критерию Стьюдента. Функция ТТЕСТ используется, чтобы определить, насколько вероятно, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же среднее (см. п. 3.5.1).

Аргументы: Массив1 – это первое множество данных. Массив2 – это второе множество данных. Хвосты – это число хвостов распределения. Если хвосты = 1, то функция ТТЕСТ использует одностороннее распределение. Если хвосты = 2, то функция ТТЕСТ использует двустороннее распределение. Тип – это вид исполняемого t-теста.

Тип	Выполняемый тест
1	Парный
2	Двухвыборочный с равными дисперсиями
3	Двухвыборочный с неравными дисперсиями

Использование функции ТТЕСТ проиллюстрируем решением некоторых примеров из главы 3.

В примере 3.6 требовалось оценить гипотезу о том, что механическая прочность окатышей при использовании новой и старой технологии их обжига не изменилась. В качестве входных данных мы имеем результаты восьми испытаний механической прочности по новой и старой технологии, т.е. два массива по 8 наблюдений. Если расположить эти массивы в электронной таблице с адресами А1:A8 и B1:B8, то после вызова функции ТТЕСТ получаем

ТТЕСТ(А1:A8;B1:B8;2;3)=0,78.

Полученный результат можно интерпретировать следующим образом. Вероятность того, что средняя механическая прочность окатышей, полученных по новой и старой технологии их обжига, не изменилась составляет не менее 78%. Это подтверждает сделанный вывод ранее при рассмотрении примера 3.6.

В качестве замечания отметим, что при тестировании мы использовали двустороннее распределение Стьюдента и тип теста – двухвыборочный с неравными дисперсиями, поскольку предварительный анализ о поведении дисперсий выборок не проводили. Читателю предлагается самостоятельно поэкспериментировать с различными типами тестов и попытаться объяснить различия в полученных результатах.

В примере 3.7 оценивались результаты испытаний на сжатие проб бетона, взятых из двух различных партий. Из первой партии было взято 8 проб, из второй – 17 проб. Расположим результаты испытаний из первой партии в массиве электронной таблицы по адресу А1:А8, а из второй партии – в массиве с адресом B1:B17. Тогда в результате вызова функции ТТЕСТ получим

ТТЕСТ(А1:A8;B1:B17;2;3)=0,02.

Следовательно, вероятность того, что свойства бетона из двух партий не изменились, крайне низка и составляет 2%. Это заключение не противоречит выводу, сделанному нами ранее при рассмотрении примера 3.7.

ФИШЕР(x)

Результат: Возвращает преобразование Фишера для аргумента x. Это преобразование строит функцию, которая имеет приблизительно нормальное, а не асимметрическое распределение. Эта функция используется для тестирования гипотез с помощью коэффициента корреляции.

Аргументы: X – это числовое значение коэффициента корреляции, которое требуется преобразовать по выражению (4.22).

В примере 4.1 с помощью функции ФИШЕР определили преобразованное значение коэффициента корреляции r_xy=0,94 – величину Z*:

Z*=ФИШЕР(0,94)=1,738.

ФИШЕРОБР(y)

Результат: Возвращает обратное преобразование Фишера. Это преобразование используется при анализе корреляции между массивами или интервалами данных. Если y = ФИШЕР(x), то ФИШЕРОБР(y) = x.

Аргументы: Y – это значение, для которого производится обратное преобразование. Уравнение для обратного преобразования Фишера имеет следующий вид:

Обратное преобразование Фишера использовалось нами ранее (см. пример 4.11) с целью определения доверительного интервала для коэффициента корреляции. В ходе решения было получено, что истинное значение величины неизвестной Z с вероятностью 95% лежит в интервале 1,215<Z<2,261, и в дальнейшем потребовалось оценить доверительные границы для коэффициента корреляции r_xy:

ФИШЕРОБР(1,215)=0,84;

ФИШЕРОБР(2,261)=0,98.

В итоге, истинное значение коэффициента корреляции с вероятностью 95% лежит в интервале -0,84 < r_xy< -0,98. Здесь мы поставили знак "-", поскольку выборочный коэффициент корреляции, по условию задачи, отрицательный.

ХИ2ОБР(вероятность; степени_свободы)

Результат: Возвращает значение обратное к односторонней вероятности распределения²(хи-квадрат). Если вероятность = ХИ2РАСП(x;...), то ХИ2ОБР(вероятность;...) = x.

Аргументы: Вероятность – это вероятность Р, связанная с распределением²(хи-квадрат). Степени_свободы – это число степеней свободы. ХИ2ОБР использует метод итераций для вычисления значения. Если задано значение вероятности Р, то функция ХИ2ОБР производит итерации, пока не получит результат с точностью ± 310⁷. Если ХИ2ОБР не сходится после 100 итераций, то функция возвращает значение ошибки #Н/Д.

Функцию ХИ2ОБР полезно использовать с целью получения теоретического значения критерия ²(критерия Пирсона) в задачах по определению доверительного интервала для дисперсии, а также при оценке обоснованности статистических гипотез.

В примере 3.4 (см. п. 3.4.2) требовалось оценить величину доверительного интервала для дисперсии по результатам десяти измерений. Для определения верхней и нижней границы доверительного интервала мы рассчитали критерии ²₁с надежностью и₁=0,05 и²₂с надежностью₂=0,95:

²₁= ХИ2ОБР(0,05;9)=16,919;

²₂= ХИ2ОБР(0,95;9)=3,325.

В примере 3.11 (см. п. 3.7) с помощью функции ХИ2ОБР мы получили теоретическое значение критерия Пирсона ²_теор=ХИ2ОБР(0,05;5)=11,07 для проверки гипотезы о том, что содержание кремния в пробах чугуна подчиняется нормальному закону распределения.

ХИ2РАСП(x; степени_свободы)

Результат: Возвращает одностороннюю вероятность (Р) распределения²(хи-квадрат, распределения Пирсона). Распределение²связано с критерием². Критерий², как было показано ранее, используется для проверки гипотезы о согласованности распределений, полученных по данным выборки с некоторой теоретической плотностью распределения (см. п. 3.7).

Аргументы: X – это значение, для которого требуется вычислить распределение. Степени_свободы – это число степеней свободы. ХИ2РАСП вычисляется как ХИ2РАСП = P(X>x), где X – это²-случайная величина.

ЧАСТОТА(массив_данных; массив_карманов)

Результат: Вычисляет частоту появления значений в интервале значений и возвращает массив цифр. Функция ЧАСТОТА может быть использована, например, при оценке нормальности распределения выборки для подсчета количества отдельных результатов измерений, попадающих в интервалы этих результатов (см. пример 3.11). Поскольку данная функция возвращает массив, она должна задаваться в качестве формулы массива. Чтобы ввести формулу массива, необходимо после выделения интервала смежных ячеек, в которые нужно вернуть полученный массив распределения, нажать [Ctrl]+[Shift]+[Enter].

Аргументы: Массив_данных – это массив или ссылка на множество данных, для которых вычисляются частоты. Если массив_данных не содержит значений, то функция ЧАСТОТА возвращает массив нулей. Массив_карманов – это массив или ссылка на множество интервалов, в которые группируются значения аргумента массив_данных. Если массив_карманов не содержит значений, то функция ЧАСТОТА возвращает количество элементов в аргументе массив_данных.

ЭКСЦЕСС(число1; число2; ...)

Результат: Возвращает эксцесс множества данных. Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительный эксцесс обозначает относительно остроконечное распределение. Отрицательный эксцесс обозначает относительно сглаженное распределение.

Аргументы: Число1, число2, ... – это от 1 до 30 аргументов, для которых вычисляется эксцесс. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой. Эксцесс определяется следующим образом:

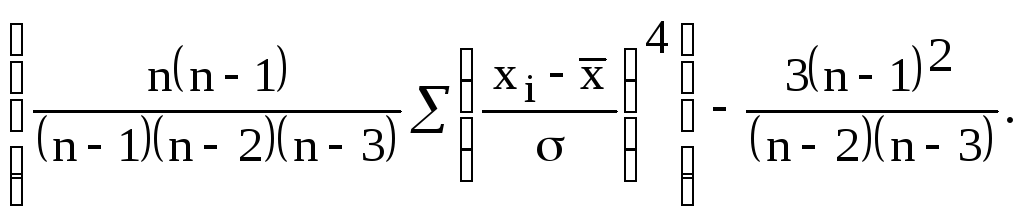
где: – стандартное отклонение выборки.

FРАСП(x;степени_свободы1;степени_свободы2)

Результат: Возвращает F-распределение вероятности (распределение Фишера). Аргументы: X – это значение, для которого вычисляется функция. Степени_свободы1 – это числитель степеней свободы. Степени_свободы2 – это знаменатель степеней свободы.

FРАСП вычисляется следующим образом: FРАСП=P(F<x), где F – это случайная величина, которая имеет F-распределение.

FРАСПОБР(вероятность;степени_свободы1;степени_свободы2)

Результат: Возвращает обратное значение для F-распределения вероятностей (критерий Фишера). Если p=FРАСП(x;...), то FРАСПОБР(p;...)=x.

Аргументы: Вероятность – это вероятность, связанная с F-распределением. Степени_свободы1 – это числитель степеней свободы. Степени_свободы2 – это знаменатель степеней свободы.

Функция FРАСПОБР использует метод итераций для вычисления значения. Если задано значение вероятности, то функция FРАСПОБР производит итерации, пока не получит результат с точностью ± 310⁷. Если FРАСПОБР не сходится после 100 итераций, то функция возвращает значение ошибки #Н/Д.

Функцию FРАСПОБР используют, чтобы определить критические значения F-распределения (например, теоретическое значение критерия Фишера при оценке адекватности математической модели или при сравнении двух дисперсий). Чтобы проиллюстрировать использование функции FРАСПОБР, воспользуемся данными из примера 3.8 (см. п. 3.5.2), в котором требовалось оценить качество измерений нового прибора в сравнении со старым прибором путем проверки статистической гипотезы о равенстве дисперсий их измерений. В ходе проверки потребовалось определить теоретическое значение критерия Фишера при уровне значимости =0,05 и степенях свободы 199 и 14:

Fтеор = FРАС7.2. Краткое описание системы STATISTICA