
- •Вопросы экзамена по математическому анализу для студентов 1 курса экономического факультета анх
- •Вопрос 1: множества и операции над ними
- •Вопрос 2 : декартово произведение множеств, бинарные отношения
- •Вопрос 3: отображения и их свойства
- •Вопрос 4: множество действительных чисел. Аксиома отделимости
- •§1. Натуральные числа
- •§ 1΄. Аксиомы Пеано
- •§ 2. Целые числа
- •§ 3. Рациональные числа
- •§4. Действительные числа
- •Вопрос 5:верхняя и нижняя грани
- •2. Стягивающиеся отрезки
- •Вопрос 6. Предельные точки
- •Вопрос 7. Приближённые вычисления
- •Вопрос 8. Предел последовательности. Предел функции. Бесконечно малые величины .Арифметические свойства предела
- •Вопрос 9. Предельный переход в неравенствах. Вычисление
- •Вопрос 10: предел монотонной ограниченной функции
- •Вопрос 11: число e
- •Вопрос 12: критерий коши существования предела последовательности, предела функции
- •Вопрос 13: непрерывность. Точки разрыва.Свойства непрерывных функций
- •1. Непрерывна в точке ;
- •2. Существует такая , что.
- •Вопрос 14: непрерывность элементарных функций
- •Вопрос 15: символы ,. Вычисление ,,
- •Вопрос 16: промежуточные значения непрерывной на отрезке функции
- •Вопрос 17: ограниченность непрерывной на отрезке функции
- •Вопрос 18: равномерная непрерывность
- •Вопрос 19: производная, её естественнонаучный смысл и основные свойства
- •1. Дифференцируемость функции
- •2.Производная
- •3. Касательная к графику функции
- •4. Правила дифференцирования
- •4. Производная обратной функции
- •6. Производная сложной функции
- •7. Производная функции, заданной параметрически
- •Вопрос 20: дифференциал. Инвариантность формы первого дифференциала
- •1.Понятие дифференциала числовой функции
- •4.Дифференциал суммы, произведения и частного функций.
- •Вопрос 21:производные и дифференциалы высших порядков
- •1. Последовательные производные
- •2. Примеры
- •3. Линейное свойство производных высших порядков
- •Вопрос 22.
- •Вопрос 23: теоремы ферма, ролля. Необходимые условия экстремума
- •Вопрос 24:теоремы лагранжа, коши.Критерий постоянства функции
- •Вопрос 25: формула тейлора с остаточным членом в форме лагранжа
- •Вопрос 26. Формула тейлора с остаточным членом в форме пеано
- •Вопрос 28: правила лопиталя
- •1. Неопределённость типа
- •Вопрос 29: монотонность функции. Достаточные условия экстремума функции
- •Вопрос 30. Функции спроса торнквиста. Функция полезности. Выпуклость графикафункции.
- •2.Производственные функции.
- •5. Выпуклость графика функции.
- •Необязательный материал, но знание его весьма полезно
- •1.Выпуклость непрерывной функции
- •2. Выпуклость дифференцируемой функции
- •3. Выпуклость дважды дифференцируемой функции
- •4.Точки перегиба
- •31. Пространство , множества в нем.
- •Вопрос32.Функции и отображения. Предел, непрерывность.
- •Функции Кобба-Дугласа.
- •Вопрос 33. Дифференцируемость функции многих переменных. Частные производные
- •Вопрос 34.
- •Вопрос 35.
- •Производная сложной функции. Инвариантность формы первого дифференциала.
- •Вопрос 36. Касательная плоскость
- •Вопрос 37. Производная по направлению, градиент.
- •Необязательный материал, но знание его весьма полезно Матрица Якоби и ее свойства.
- •Вопрос 39. Производные высших порядков
- •Дифференциалы высших порядков
- •Второй дифференциал функции.
- •Вопрос 41. Формулы Тейлора.
- •Билет 42. Экстремумы функций нескольких переменных.
- •Достаточные условия экстремума.
- •Метод наименьших квадратов.
Вопрос 5:верхняя и нижняя грани
Определение
5.1. Множество
A ограничено
сверху,
если существует такое число M, что
![]() .
При этом число M называется верхней
границей
или гранью
множества A. Множество A
ограничено
снизу,
если существует такое число m, что
.
При этом число M называется верхней
границей
или гранью
множества A. Множество A
ограничено
снизу,
если существует такое число m, что
![]() .
При этом число m называется
нижней
границей
или гранью
множества A.
.
При этом число m называется
нижней
границей
или гранью
множества A.
Легко видеть, что если множество A ограничено сверху (снизу), то любое число, большее M (меньшее m) тоже будет его верхней (нижней) границей.
Определение 5.2. Если множество A ограничено сверху, то наименьшая из его верхних граней называется точной верхней гранью A и обозначается sup A.
Теорема 5.1. Если множество A ограничено сверху, то существует точная верхняя грань этого множества.
Доказательство.
Выберем
множество B
таким,
что
![]() (т.е.B
– это множество всех верхних граней
А).
Докажем, что множество
В имеет
наименьший элемент. По аксиоме отделимости
(см. билет 4) существует такое
(т.е.B
– это множество всех верхних граней
А).
Докажем, что множество
В имеет
наименьший элемент. По аксиоме отделимости
(см. билет 4) существует такое
![]() ,
что
,
что![]() .
Так как для всех
.
Так как для всех![]() имеем
имеем![]() ,
числоc
является верхней гранью А.
Так как для всех
,
числоc
является верхней гранью А.
Так как для всех
![]() ,
числоc
– наименьшее среди элементов множества
B.
Таким
образом,
,
числоc
– наименьшее среди элементов множества
B.
Таким
образом,
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Определение 5.3.Если множество A ограничено снизу, то наибольшая из его нижних граней называется точной нижней гранью А и обозначается inf A.
Теорема 5.2 Если множество A ограничено снизу, то существует точная нижняя грань этого множества.
Доказательство . Доказательство можно провести двумя способами.
1
способ.
По аналогии с теоремой 5.1. рассмотреть
множество D
нижних граней множества A.
Применить аксиому отделимости к D
и А.
По аксиоме отделимости (см. билет 4)
существует такое
![]() ,
что для всех
,
что для всех![]() ,
для всех
,
для всех![]() имеет место неравенство
имеет место неравенство![]() .
Так как для всех
.
Так как для всех![]() выполняется неравенство
выполняется неравенство![]() ,d
является
нижней гранью А.
Так как для всех
,d
является
нижней гранью А.
Так как для всех
![]() имеем
имеем![]() ,d –
наибольшая среди нижних граней множества
А,
т.е.
,d –
наибольшая среди нижних граней множества
А,
т.е.
![]() .
.
2
способ.
Определим множество -A
так:
![]() .
ЕслиA
ограничено снизу, то -A
ограничено сверху, поэтому
.
ЕслиA
ограничено снизу, то -A
ограничено сверху, поэтому
![]() ,
кроме того,
,
кроме того,![]() .
.
2. Стягивающиеся отрезки
Определение
5.4. Система
отрезков
![]() называется
вложенной,
если
называется
вложенной,
если
![]() .
.
Теорема
5.3
Любая
вложенная система отрезков имеет хотя
бы одну общую для всех отрезков точку,
т.е.
![]() :
:
![]() .Иными
словами,
.Иными
словами,
![]() :
:![]() или
или![]() Ø.
Ø.
Доказательство. Выберем множества A и B так, что
![]() ,
,
![]() .
Для того чтобы применить аксиому
отделимости, необходимо доказать, что
.
Для того чтобы применить аксиому
отделимости, необходимо доказать, что
![]() выполняются неравенства
выполняются неравенства![]() .
.
Выберем
m
так, что![]() .
Тогда
.
Тогда![]() ,
,![]() .
Значит,
.
Значит,
![]() :
:
![]()
![]() ,
полагая
,
полагая![]() ,
получим:
,
получим:![]() .
Таким образом,c
- общая для всех отрезков точка. Теорема
доказана.
.
Таким образом,c
- общая для всех отрезков точка. Теорема
доказана.
Определение
5.5. Система
отрезков![]() называется
стягивающейся
системой
отрезков, если длины этих отрезков
стремятся к 0 при
называется
стягивающейся
системой
отрезков, если длины этих отрезков
стремятся к 0 при
![]() ,
т.е.
,
т.е.
![]() .
.
Теорема 5.4. Общая точка стягивающейся системы отрезков единственна.
Доказательство.
Допустим,
что есть 2 общие точки
![]() .
Тогда
.
Тогда
![]() .
Возьмем
.
Возьмем
![]() .
Найдется такое
.
Найдется такое
![]() ,
что для любого
,
что для любого
![]()
![]() .
.
Одновременно получаем, что
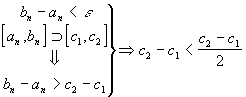 ,
откуда
,
откуда
![]() .
Но
.
Но
![]() .
Тем самым, мы пришли к противоречию.
Теорема доказана.
.
Тем самым, мы пришли к противоречию.
Теорема доказана.
Замечания:
точка c является точной верхней гранью множества левых отрезков и точной нижней гранью множества правых концов этих отрезков.
вложенная система интервалов может не иметь общую точку, как показывает
Пример:
Рассмотрим
![]() У этих интервалов нет общей точки –
докажем это от противного. Если бы общая
точка
У этих интервалов нет общей точки –
докажем это от противного. Если бы общая
точка![]() была, то она принадлежала бы первому
интервалу, т.е.
была, то она принадлежала бы первому
интервалу, т.е.![]() ,
,![]() .
Выберем число
.
Выберем число![]() так, чтобы
так, чтобы![]() ,
т.е.
,
т.е.![]() .
Тогда
.
Тогда![]() вопреки предположению.
вопреки предположению.
